Захаров М.А

11

Примеры решения задач

Задача 2.1

Какие из следующих функций отвечают требованиям, предъявляемым к волновым функциям, и в какой области изменения аргумента:

а) Ψ ( x ) = C exp(αr ) , где 0 < r < ∞ ;

b)Ψ ( x ) = C sinαx ;

c)Ψ ( x ) = C Arc sin x ?

Решение задачи

Волновая функция должна быть непрерывной, конечной и однозначной во всей области определения.

a) Функция Ψ ( x ) = C exp(αr ) , где 0 < r < ∞ , является однозначной и не-

прерывной на всем указанном промежутке. Однако при α > 0 данная функция неограниченно возрастает при r → ∞ . Заметим, что при α < 0 данная функция удовлетворяет всем требованиям, предъявляемым к волновым функциям.

b) Функция Ψ ( x ) = C sinαx отвечает всем требованиям, предъявляе-

мым к волновым функциям.

c) Функция Ψ ( x ) = C Arc sin x является неоднозначной, поэтому в об-

щем случае она не отвечает указанным выше требованиям. Тем не менее, мож-

но заметить, что на промежутке − π / 2 ≤ x ≤ π / 2 данная функция становится однозначной.

Ответ: a) удовлетворяет требованиям при значениях параметра α < 0 ;

b)удовлетворяет всем требованиям;

c)удовлетворяет требованиям на промежутке − π / 2 ≤ x ≤ π / 2 .

12

Задача 2.2

Частица находится в состоянии, описываемом функцией

Вероятность нахождения частицы в элементе длины dx согласно (2.1)

определяется выражением dW = Ψ ( x ) 2 dx . Поэтому определение вероятности

Ответ: 0.61.

Задача 2.3

Какие из перечисленных функций удовлетворяют требования к функции

плотности вероятности:

a)Ψ ( x ) = eix ;

b)Ψ ( x ) = xe− x2 ;

c)Ψ ( x ) = e− x2 ?

13

Решение задачи

Функция плотности вероятности должна быть непрерывной, веществен-

ной и неотрицательной функцией. Кроме того, она должна быть нормирована на единицу. Пользуясь этими свойствами, обратимся к условию задачи.

a) Нетрудно видеть, что функция Ψ ( x ) = eix – комплексозначная, что противоречит свойствам функции плотности вероятности.

b) Заметим, что при отрицательных значениях аргумента функция

Ψ ( x ) = xe− x2 оказывается отрицательной, что также противоречит свойствам функции плотности вероятности.

c) Функция Ψ ( x ) = e− x2 , будучи непрерывной, вещественной и неотри-

цательной, тем не менее также не удовлетворяет указанным выше свойствам,

поскольку данная функция не нормирована на единицу.

Ответ: ни одна из функций не удовлетворяет.

Задачи для самостоятельного решения

2.4.Определите нормировочную C постоянную для волновой функции вида Ψ ( x ) = C exp( −αx2 ) .

2.5.Определите наиболее вероятное положение и среднее и значение координаты частицы, находящейся в бесконечно глубокой потенциальной яме в основном и первом возбужденном состоянии. Волновые функции частицы

2 / l sin( πnx / l ), где l – ширина ямы.

2.6. Определите наиболее вероятное положение и среднеквадратичное значение координаты частицы, совершающей малые колебания у положения равновесия, в основном и первом возбужденном состоянии. Волновые функции частицы имеют вид:

H0 = 1, H1 = 2ξ .

2.7.Определите вероятность нахождения частицы, совершающей малые колебания у положения равновесия в области x = a0 ± 0.01a0 в основном и пер-

вом возбужденном состоянии.

2.8. Определите наиболее вероятное положение электрона в атоме водо-

рода в основном и первом возбужденном состоянии. Радиальные части волно-

вых функций электрона в атоме водорода имеют вид

Сравните полученные результаты с результатами, вытекающими из тео-

рии Бора.

ТЕМА 3. ОПЕРАТОРЫ И ИХ СВОЙСТВА

В квантовой механике каждой физической величине A сопоставляют

оператор таким образом, чтобы среднее значение было равно

где интегрирование проводится по всему пространству.

Поскольку в квантовой механике операторы соответствуют реальным физическим величинам, то на них накладываются определенные условия. Опе-

раторы, соответствующие физическим величинам, должны быть линейными и эрмитовыми.

Оператор называется линейным, если выполняются условия

Эрмитовость оператора вытекает из условия вещественности физических величин, т.е. для всех измеряемых на опыте (средних) значений физических ве-

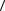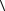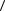личин выполняется соотношение A = A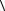 . Это накладывает следующие усло-

вия для операторов:

операторы в общем случае не коммутируют. По определению, коммутатором

Если коммутатор двух операторов равен нулю, то говорят, что операто-

ры коммутируют друг с другом, т.е. их действие на функцию не зависит от по-

рядка сомножителей.

Если A и B две физические величины, которые одновременно имеют определенные значения, то можно показать, что соответствующие им операто-

ры коммутативны. Справедливо и обратное утверждение, а именно, если ком-

мутатор двух операторов равен нулю, то соответствующие величины могут од-

новременно иметь определенные значения.

16

Примеры решения задач

Задача 3.1

Определите результаты действия операторов на указанные функции:

Решение задачи

Действуя операторами на функции, получаем:

Задача 3.2

Коммутируют ли между собой приведенные ниже операторы:

Решение задачи

Для нахождения коммутаторов соответствующих операторов обычно используется некоторая вспомогательная (так называемая «пробная») функция,

17

взятая из области определения оператора. Находят действие коммутатора двух операторов на функцию, а затем результату действия коммутатора сопоставля-

ют соответствующий оператор. Следует помнить, что коммутатор двух опера-

торов есть оператор, а не функция, получившаяся в результате действия. В ка-

честве «пробной» функции возьмем функцию f ( x, y, z ) . Действие коммутатора на функцию будет равно:

данные операторы не коммутируют.

Ответ: a) коммутируют; b) не коммутируют; c) не коммутируют.

Задача 3.3

Какие из указанных ниже операторов являются линейными?

ˆ =

a) Af af ;

ˆ= 2

b)Af f .

18

Решение задачи

указанных выше. С этой целью введем функцию f = C1 f1 + C2 f 2 . Тогда имеем:

т.е. данный оператор не является линейный.

Ответ: a) оператор линейный; b) оператор нелинейный.

Задачи для самостоятельного решения

3.4. Определите результаты действия операторов на указанные функции:

3.5. Коммутируют ли между собой приведенные ниже операторы:

3.6. Какие из указанных ниже операторов являются линейными?

19

−∞

3.7. Можно ли одновременно точно определить:

a)x -проекцию координаты и y -проекцию импульса частицы;

b)x - и y -проекции импульса частицы;

c)x -проекцию координаты и y -проекцию момента импульса частицы;

d)x - и y -проекции момента импульса частицы;

e)x -проекцию момента импульса частицы и его величину, т.е. Lx и L ?

ТЕМА 4. СТАЦИОНАРНЫЕ СОСТОЯНИЯ

В квантовой механике очень часто приходится иметь дело с ситуацией,

когда частица находится во внешнем стационарном поле. В этом случае со-

стояние системы не будет изменяться с течением времени, т.е. система будет находиться в состояниях с определенной энергией. Волновая функция, описы-

вающая стационарное состояние системы, будет являться собственной волно-

вой функцией оператора Гамильтона ˆ т е будет удовлетворять уравнению

H , . .

где E – энергия системы.

Уравнение (4.1) получило название стационарного уравнения Шредин-

гера. Можно показать, что волновая функция, описывающая стационарные со-

стояния, имеет вид

20

где функция Ψ ( r ) определяется из решения стационарного уравнения Шре-

дингера (4.1). Таким образом, если Гамильтониан системы явно от времени не зависит, то полную волновую функцию, описывающую состояние системы,

Ψ(r , t) можно представить в виде произведения координатной части волновой

часть волновой функции находится из решения стационарного уравнения Шре-

дингера т е ˆ Ψ = Ψ

, . . H E .

Величина E имеет размерность частоты, поэтому очень часто вводят h

обозначение ω = E / h и волновую функцию, описывающую стационарные со-

стояния, записывают в виде

В общем случае уравнение Шредингера представляет собой дифферен-

циальное уравнение второго порядка в частных производных, и решить его точно удается лишь в очень ограниченных случаях. Тем не менее, эти довольно простые модели позволяют получить информацию о характере движения час-

тиц. Для более сложных случаев используют приближенные методы решения уравнения Шредингера.

4.1. Потенциальная яма

Если частица находится в области пространства, где U ( x, y, z) имеет минимум, то говорят, что частица находится в потенциальной яме.

Если движение происходит вдоль одного направления, то говорят что яма одномерная. Если стенки ямы прямые, то говорят что яма прямоугольная. В

случае, когда потенциальная энергия в пространстве изменяется по закону