
Захаров М.А
..pdf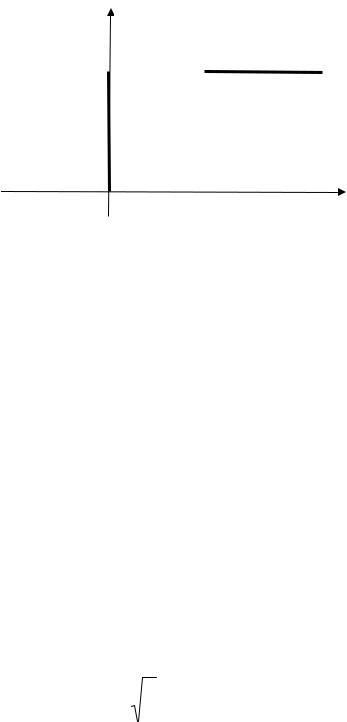
21 |
|
|
|
U 0 ; |
x < 0; |
|
|
|
|
|
|
U (x) = 0; |
|
0 < x < l; |
(4.4) |
|
; |
x < l, |
|
U 0 |
|
||
говорят, что частица находится в однородной прямоугольной потенциальной яме, схематичное изображение которой представлено на рис. 1.
U(x)
U0
I |
II |
III |
|
|
|
0 |
|
l |
X |
|
|
|
|
|
|
|
|
Рис. 1. Схематичное изображение одномерной прямоугольной потенциальной ямы
Из решения стационарного уравнения Шредингера (4.1) для бесконечно глубокой потенциальной ямы следует, что энергия частицы принимает не лю-
бые, а дискретные значения, получившие название уровни энергии, значения которых определяются выражением
En = |
h2π 2n2 |
, |
(4.5) |
|
2ml 2 |
||||
|
|
|
где n = 1, 2, 3 … – номер уровня;
m – масса частицы;
l – ширина ямы.
Волновая функция, описывающая состояние частицы в бесконечно глу-
бокой потенциальной яме, имеет вид
|
2 |
|
πnx |
|
|
Ψn ( x ) = |
|
sin |
|
. |
(4.6) |
l |
|
||||
|
|
l |
|
||

22
4.2. Потенциальный барьер
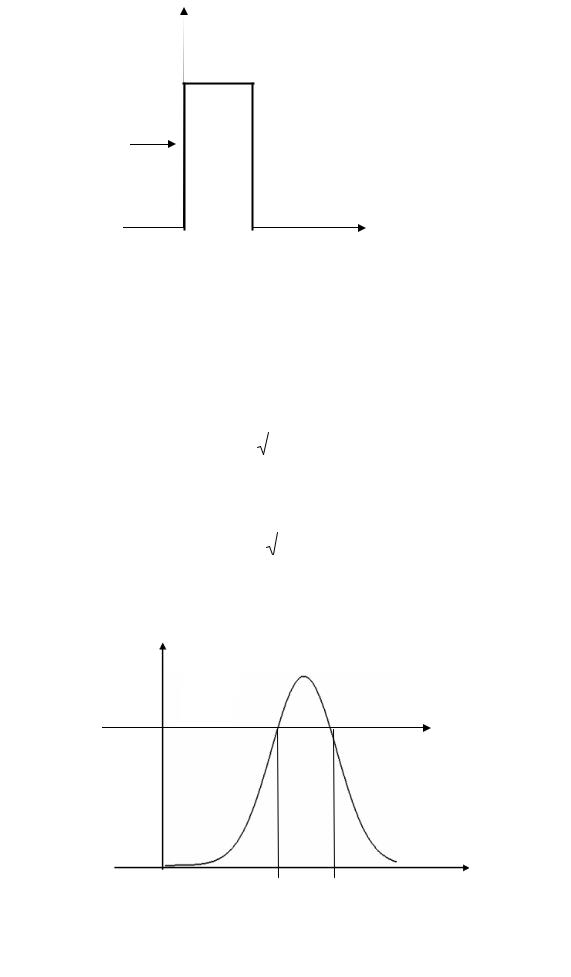
Если частица движется в области пространства и потенциальная энергия имеет вид , изображенный на рис. 2, то говорят, что частица на своем пути встречает потенциальный барьер высотой U 0 .
U(x)
U0
X
Рис. 2. Схематичное изображение потенциального барьера
В классической механике если энергия частицы больше высоты барьера
U 0 , то частица всегда окажется в области за барьером, а если меньше U 0 , то частица никогда не может преодолеть этот потенциальный барьер.
В квантовой механике имеет место несколько иная ситуация. В случае если энергия частицы больше высоты барьера, то наряду с вероятностью того,
что частица окажется в области за барьером, имеется отличная от нуля вероят-
ность того, что частица отразится от барьера, т.е. имеет место так называемое надбарьерное отражение.
Если энергия частицы меньше высоты барьера, то наряду с вероятно-
стью того, что частица отразится от барьера, имеется отличная вероятность то-
го, что частица окажется в области за барьером, так называемое подбарьерное прохождение или туннельный эффект.
23
 U(x)
U(x) 

U0
E
●
I |
|
|
II |
|
III |
|
|
|
|
|
X |
|
|
|
|
|
|
|
|
|
|
|
l |
|
0 |
|
|
||
Рис. 3. Схематичное изображение прямоугольного потенциального барьера
Можно показать, что для прямоугольного потенциального барьера вы-
сотой U 0 и шириной l , изображенного на рис. 3, вероятность прохождения час-
тицы через потенциальный барьер определяется выражением
D ≈ exp |
− 2 |
|
|
|
l . |
|
|
|
2m ( U0 |
− E ) |
(4.7) |
||||
|
|||||||
|
h |
|
|
|
|
||
Для барьера произвольной формы эта вероятность определяется выра- жением
|
− 2 |
b |
|
|
|
|
|
|
∫ |
2m (U ( x ) − E )dx |
|
, |
(4.8) |
||
D ≈ exp |
|
|
|||||
|
h |
a |
|
|
|
|
|
|
|
|
|
|
|
|
|
где a и b точки, в которых U (x) = E (рис. 4).
U(x)
E
●
a b X
Рис. 4. Схематичное изображение прохождения частицы через потенциальный барьер произвольной формы; a и b точки, в которых U (x) = E
24
4.3. Гармонический осциллятор
Если потенциальная энергия системы имеет минимум в точке x = x0 , то при малом отклонении системы от положения равновесия на нее будет дейст-
вовать «квазиупругая» (почти как упругая) сила, стремящаяся вернуть систему в положение равновесия. Квазиупругой силой называется сила, направление которой противоположно направлению смещения системы из положения рав-
новесия, а ее величина пропорциональна величине отклонения системы из по-
ложения равновесия. Действительно, разложим потенциальную энергию систе-
мы в ряд по величине отклонения с учетом первых двух членов разложения. В
результате разложения имеем
U( x ) ≈U( x )+ a( x − x )+ |
kx2 |
+..., |
(4.9) |
||||||||
|
|
|
|||||||||
|
|
0 |
0 |
2 |
|
|
|||||
|
|
|
|
|
|
|
|
||||
где введены обозначения a = |
∂U |
|
|
, k = |
∂2U |
|
|
. |
|
||
|
|
|
|
|
|||||||
|
|
|
|||||||||
|
|
|
|
|
|||||||
|
∂x |
|
x=x0 |
|
∂x |
2 |
|
|
x =x0 |
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|||
Потенциальная энергия системы, по условию, имеет минимум в точке
x = x0 . Из этого условия следует, что a = 0 , а k > 0 . Кроме того, значение по-
тенциальной энергии в положении равновесия удобно положить равным нулю.
С учетом этого, выражение для потенциальной энергии при отклонении систе-
мы от положения запишется в виде
|
k (x − x )2 |
|
|
|
U (x) = |
0 |
. |
(4.10) |
|
2 |
||||
|
|
|
Сила, возникающая при смещении системы из положения, определяется выражением
F |
= − |
∂U ( x ) |
= −k( x − x ) . |
(4.11) |
|
||||
x |
|
∂x |
0 |
|
|
|
|
|
Как видно из выражения (4.11), данная сила направлена в сторону, про-
тивоположную смещению системы из положения равновесия, а ее величина пропорциональна смещению, т.е. данная сила является квазиупругой. В качест-
25
ве примера можно указать, что при смещении атомов кристаллической решетки из положения равновесия возникающая сила является квазиупругой.
Для системы координат, начало которой совмещено с положением рав-
новесия, выражение для потенциальной энергии примет вид
U ( x ) = kx2 / 2 . |
(4.12) |
В классическом случае, при наличии квазиупругой силы (4.11), система совершает колебания около положении равновесия с круговой частотой
ω 2 |
= k / m . |
(4.13) |
0 |
|
|
Зависимость величины смещения и скорости смещения от времени да-
ется уравнениями
x( t ) = Acos( ω0t + φ ) , |
|
|
|
|
(4.14) |
||||
V ( t ) = − Aω0 sin( ω0t + ϕ ), |
|
|
(4.15) |
||||||
где A – амплитуда; |
|
|
|
|
|
|
|
|
|
ϕ – начальная фаза колебаний. |
|
|
|
|
|
|
|
|
|
Полная энергия системы определяется выражением |
|
||||||||
E = Eкин + Епот = |
mV 2 |
+ |
kx |
2 |
= |
kA2 |
|
||
|
|
|
|
. |
(4.16) |
||||
2 |
2 |
2 |
|||||||
|
|
|
|
|
|||||
Как следует из (4.16), в классическом случае энергия системы имеет не-
прерывный спектр и квадратично зависит от амплитуды колебаний. В кванто-
вом случае энергия имеет дискретный спектр собственных значений.
Выражение для потенциальной энергии системы (4.12) с учетом того,
что круговая частота связана с коэффициентом «квазиупругой» силы соотно-
шением (4.13), запишем в виде
|
|
U ( x) = mω 2 x2 |
/ 2 . |
(4.17) |
|||
|
|
|
|
|
0 |
|
|
Стационарное уравнение Шредингера в данном случае имеет вид |
|
||||||
|
h2 ∂ 2 Ψ |
mω 2 x 2 |
|
|
|||
− |
|
|
|
+ |
0 |
Ψ = EΨ . |
(4.18) |
2m |
|
∂x 2 |
2 |
||||
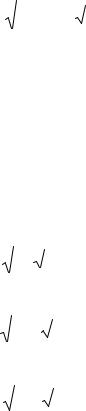
26
Из решения стационарного уравнения Шредингера (4.18) вытекает, что
энергия системы принимает дискретные значения, равные |
|
En = hω0 (n + 1 / 2) . |
(4.19) |
А волновые функции гармонического осциллятора определяются выра-
жением
Ψn ( x ) = |
|
|
|
1 |
|
|
|
H n (x / a0 ) exp |
− |
1 |
( x / a0 )2 |
, |
(4.20) |
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|||||||||
2 |
n |
n! a0 |
π |
|
|
|
2 |
|
|
|
|||
|
|
|
|
|
|
|
|
|
|||||
где H n (x / a0 ) – полиномы Чебышева–Эрмита, определяемые выражением
H |
|
( ξ ) = ( −1 )n exp(ξ 2 ) |
d n |
exp( −ξ 2 ) . |
(4.21) |
|
n |
dξ n |
|||||
|
|
|
|
|||
|
|
|
|
|
С учетом этого волновые функции, соответствующие основному, пер-
вому и второму возбужденному состоянию, имеют вид
Ψ0 (x)
Ψ1(x)
Ψ2 ( x)
|
|
1 |
|
|
|
|
|
|
|
|
1 |
|
2 |
|
|
|
||||
= |
|
|
|
|
|
|
|
|
exp − |
|
( x / a0 ) |
|
, |
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
a0 |
π |
|
|
|
|
2 |
|
|
|
|
|
|||||
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
1 |
|
2 |
|
|||
= |
|
|
|
|
|
|
|
|
|
|
|
2(x / a0 ) exp − |
|
|
(x / a0 ) |
|
, |
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
2a0 |
π |
|
|
|
|
|
|
|
2 |
|
|
|
|||||
|
|
1 |
|
2 |
|
|
1 |
|
2 |
|
||
= |
|
|
|
|
|
(4(x / a0 ) |
− 2) exp |
− |
|
(x / a0 ) |
|
. |
|
|
|
|
|
|
|
||||||
|
|
|
|
|
||||||||
|
|
|
|
|||||||||
|
|
8a0 π |
|
|
|
|
|
2 |
|
|
|
|
(4.22)
(4.23)
(4.24)
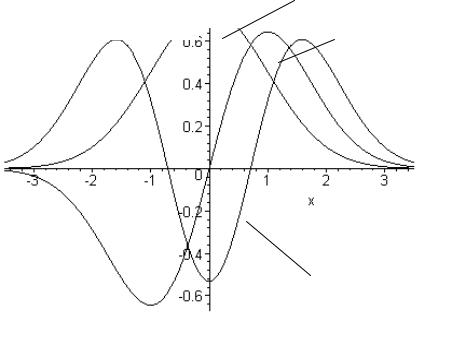
Графики этих функций представлены на рис. 7. Как видно из рисунка, в основ-
ном состоянии наиболее вероятным положением частицы, совершающей коле-
бания, является точка x = 0 , в то время как в первом возбужденном состоянии наиболее вероятными положениями являются точки x = ±a0 .
27
n=0
Ψ(x/a0)
n=1
x/a0
n=2
Рис. 5. Волновые функции основного (n = 0) и первых двух возбужденных (n = 1, 2) состояний гармонического осциллятора
Примером систем, являющимися гармоническими осцилляторами, яв-
ляются атомы, совершающие малые колебания около положения равновесия в молекулах или твердых телах.
Примеры решения задач
Задача 4.1
Для частицы, находящейся в бесконечно глубокой потенциальной яме,
найти среднее значение и флуктуацию координаты частицы. При решении за-
дачи воспользоваться волновой функцией (4.6).
Решение задачи
Для нахождения среднего значения координаты частицы воспользуемся общим квантовомеханическим правилом вычисления средних значений физи-
ческих величин

28 |
|
x = ∫Ψ * ( x )xΨ ( x )dx . |
(4.25) |
Учитывая, что волновые функции отличны от нуля лишь на промежутке
0 < x < a , найдем
a |
2 |
x sin2 |
πnx |
|
a |
|
|
|
x = ∫ |
dx = |
. |
(4.26) |
|||||
|
a |
|
||||||
0 |
a |
2 |
|
|
||||
|
|
|
|
|
|
|
||
Для нахождения флуктуации координаты введем вначале отклонение координаты от своего среднего значения, т.е.
|
|
|
|
|
|
|
|
|
|
x = x − x . |
|
|
|
(4.27) |
||
|
|
Очевидно, что среднее значение |
|
|
|
|
||||||||||
|
|
|
|
|
< |
x >=< x − x >= 0 , |
|
|
|
(4.28) |
||||||
поэтому |
для |
характеристики |
флуктуаций |
используют |
величину |
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
δx |
ср.кв. |
= |
x2 = |
( x − x )2 , получившую название |
среднее квадратическое |
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
отклонение. |
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
Используя это определение, имеем |
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
δxср.кв. = ( x)2 = |
|
x2 |
− 2 x x − x 2 |
= x2 − x 2 . |
(4.29) |
||||||||
Таким образом, для вычисления флуктуации координаты частицы необ-
ходимо найти величину
x2 = ∫Ψ * ( x )x2Ψ ( x )dx . |
(4.30) |
Подставляя в последнее соотношение волновые функции стационарных состояний, получим
|
2 |
= a |
2 |
|
1 |
− |
|
1 |
|
|
|
|
x |
|
|
|
|
|
|
|
|
. |
(4.31) |
||
|
|
|
2π |
2 |
n |
2 |
||||||
|
|
|
|
3 |
|
|
|
|
|
|||
Тогда
|
|
|
a |
|
1 |
|
|
2 |
|
|
|
|
δxср.кв. = ( x)2 |
= |
− |
|
|
|
|||||||
|
|
|
|
|
|
|
. |
(4.32) |
||||
2 |
|
π |
2 |
n |
2 |
|||||||
|
|
|
3 |
|
|
|
|
|
||||

29
Легко видеть, что с увеличением номера состояния флуктуация коорди-
наты увеличивается, приближаясь к максимальному значению
max( δxср.кв. ) = |
|
a |
|
|
≈ 0.28a . |
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
12 |
|
|
|
|
|
|
|
|
|
|
|
|||||||
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
x = |
|
|
a |
a |
|
|
1 |
|
|
2 |
|
|
||||
Ответ: |
|
|
|
, δxср.кв. = |
|
|
|
|
− |
|
|
|
|
. |
||||
2 |
2 |
|
π |
2 |
n |
2 |
||||||||||||
|
|
|
|
|
|
3 |
|
|
|
|
||||||||
Задача 4.2
Найти уровни энергии и нормированные волновые функции состояний дискретного спектра частицы в поле U ( x ) = −αδ ( x ), для значений параметра
α > 0. Найти средние значения кинетической и потенциальной энергий в этих состояниях.
Решение задачи
Запишем стационарное уравнение Шредингера с учетом явного вида оператора потенциальной энергии
− |
h |
2 |
Ψ ' ' ( x ) − αδ ( x )Ψ ( x ) = EΨ ( x ). |
(4.33) |
|
|
|||
|
|
|||
|
2m |
|
||
Заметим, что связанные состояния частицы в указанном внешнем поле могут быть лишь при условии E < 0.
Введем обозначение
|
β 2 = − |
2mE |
. |
|
(4.34) |
|
|
|
|||||
|
|
|
h2 |
|
|
|
Тогда уравнение Шредингера примет вид |
|
|||||
Ψ '' ( x ) + |
2m |
− β 2Ψ ( x ) = 0. |
|
|||
|
αδ ( x )Ψ ( x ) |
(4.35) |
||||
h2 |
||||||
Общее решение уравнения Шредингера в области − ∞ < x < 0 имеет вид
Ψ1( x ) = Aeβx + Be−βx . |
(4.36) |
30
Сдругой стороны, волновая функция должна стремиться к нулю при x → −∞. Для выполнения этого условия необходимо, чтобы B = 0. Отсюда в об-
ласти − ∞ < x < 0 волновая функция имеет вид
Ψ1( x ) = Ae βx . |
(4.37) |
Рассуждая аналогичным образом, нетрудно получить общее решение уравнения Шредингера для области 0 < x < +∞ :
Ψ2( x ) = Ceβx + De−βx . |
(4.38) |
Найденное решение должно стремиться к нулю при x → +∞. Для выполнения этого условия необходимо, чтобы C = 0. Отсюда в области 0 < x < +∞ волновая функция имеет вид
Ψ2( x ) = De−βx . |
(4.39) |
Из условия непрерывности волновой функции на всей области опреде- |
|
ления имеем |
|
Ψ1 (0)=Ψ 2 ( 0 ), |
(4.40) |
откуда следует, что A = D.
Теперь исследуем поведение первой производной найденной волновой функции в окрестности x = 0. С этой целью проинтегрируем исходное уравнение
Шредингера по области 0 − ε < x < 0 + ε , ε > 0 , и, устремляя ε → 0, находим
|
|
Ψ ' ( 0 + ε ) −Ψ ' ( 0 − ε ) + |
2m |
αΨ ( 0 ) = 0. |
(4.41) |
||
|
|
|
|||||
|
|
|
h2 |
|
|
|
|
|
Таким образом, производная волновой функции терпит разрыв в точке |
||||||
x = 0. Отсюда следует, что параметр β принимает только одно |
значение |
||||||
β = |
mα |
. Поскольку параметр β связан с энергией соотношением β 2 |
= − |
2mE |
, |
||
|
|
||||||
|
h2 |
|
|
|
|
h2 |
|
то отсюда следует, что существует только одно состояние дискретного спектра,
которое характеризуется энергией
E |
= − |
mα 2 |
. |
(4.42) |
|
|
|
||||
0 |
2h |
2 |
|
|
|
|
|
|
|
||
