Захаров М.А

31

При этом сама волновая функция (с учетом нормировки на единицу)

принимает вид

Наконец, используя общие квантовомеханические формулы вычисления средних, нетрудно получить средние значения потенциальной и кинетической энергий частицы в рассматриваемом состоянии:

Задача 4.3

Определите коэффициент отражения частицы от прямоугольной потенци-

альной ступеньки высотой U0 для случая, когда энергия частицы E = 2U0 .

Решение задачи

Будем считать, что ступенька расположена в точке x = 0 и зависимость потенциальной энергии от координат имеет вид

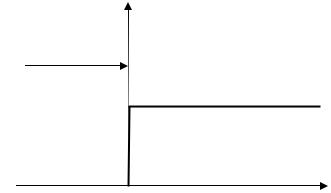
32

Эта зависимость схематично представлена на рис. 6.

U(x)

E

●

U0

X

0

Рис. 6. Схематичное изображение частицы, налетающей на потенциальную стенку высотой U0

В классической физике если частица налетает с энергией, большей чем высота ступеньки, то она всегда окажется во второй области, т.е. вероятность отражения от ступеньки равна нулю. В квантовой механике если частица нале-

тает на ступеньку с энергией больше высоты ступеньки, то наряду с тем, что частица окажется в области за границей ступеньки, имеется отличная от нуля вероятность того, что частица отразится от ступеньки. Для того чтобы опреде-

лить эту вероятность, решим стационарное уравнение Шредингера для данной

зависимости потенциальной энергии от координат.

Уравнение Шредингера для I и II области примет следующую форму

Перенося все члены уравнений в правую часть и, разделив на коэффи-

циент при старшей производной, получим

33

Решения уравнений (4.48) и (4.49) с учетом того, что во второй области волновая функция описывает только частицу, движущуюся слева направо, за-

пишем в виде

Уравнение (4.50) описывает движение частицы в первой области, при-

чем первый член описывает движение слева направо (падающая волна), а вто-

рой – справа налево (отраженная волна). Аналогично член в правой части урав-

нения (4.51) описывает прошедшую волну, т.е. соответствует частице, движу-

щейся за ступенькой.

По определению, коэффициентом отражения R называется величина,

равная отношению плотности потока отразившихся от барьера частиц к плот-

ности потока падающих частиц, т.е.

Коэффициентом прохождения D , или прозрачностью потенциального барьера, называется величина, равная отношению плотности потока прошед-

ших через барьер частиц к плотности потока падающих частиц, т.е.

Очевидно, что между этими коэффициентами имеет место соотношение

R + D =1.

Плотность потока вероятности частиц определяется выражением

34

Используя это определение и выражения для волновых функций в пер-

вой (4.50) и третьей (4.51) областях для падающего, отраженного и прошедшего потоков, получим выражения

Для того чтобы вычислить постоянные интегрирования A1 , B1 , A2 ,

воспользуемся условиями непрерывности волновой функции и ее первой произ-

35

Решая систему, для коэффициентов получим следующие выражения:

b1 = ( k1 − k2 ) /( k1 + k2 ).

С учетом этого для коэффициента отражения R после несложных пре-

образований получим уравнение

Подставляя числовое значение γ = 2 (по условию задачи), для коэффициента отражения получим R ≈ 0.03 . Таким образом, при энергии частицы в два раза превышающей высоту ступеньки 3% частиц испытывают отражение.

Ответ: R ≈ 0.03 .

Задачи для самостоятельного решения

4.4. Найдите волновые функции стационарных состояний для свободной частицы, движение которой ограничено непроницаемой стенкой, т.е. потенци-

альная энергия имеет вид

4.5. Определите коэффициент отражения частицы от прямоугольного потенциального барьера высотой U0 = 1.5эВ и шириной l = 5нм , если энергия налетающей частицы равна E = 0.7 эВ.

4.6. Выведите формулу для коэффициента отражения частицы от двух прямоугольных потенциальных барьеров высотой U1 и U 2 соответственно и шириной l1 и l2 , если энергия налетающей частицы меньше высоты каждого из барьеров, т.е. E < U1 и E < U1 (см. рис. 7).

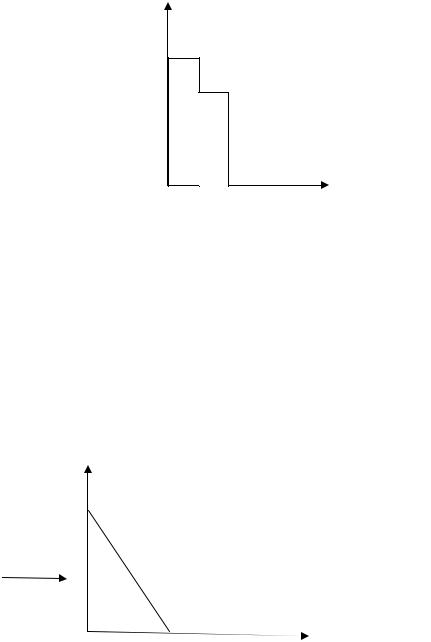
36

U(x)

U1

U2

Е

•

Рис. 7. Схематичное изображение частицы, налетающей на два потенциальных барьера высотой U1 и U2 соответственно

4.7. Выведите формулу для коэффициента прохождения частицы через треугольный потенциальный барьер высотой U0 и U 2 и шириной l и l2 , если энергия налетающей частицы меньше высоты барьера, т.е. E <U0 и E <U1 (см.

рис. 8). Указание: при решении задачи воспользуйтесь формулой (4.8).

U(x)

Е

•

Рис. 8. Схематичное изображение частицы, налетающей на треугольный потенциальный барьер высотой U0 и шириной l

4.8. Выведите формулу для среднего значения координаты и ее среднего

квадратического отклонения гармонического осциллятора в основном и первом

возбужденном состояниях.

37

Тема 5. СТАЦИОНАРНАЯ ТЕОРИЯ ВОЗМУЩЕНИЙ

Решить уравнение Шредингера точно удается в очень ограниченном числе простейших случаев. Однако в целом ряде случаев удается найти при-

ближенное решение уравнения Шредингера. Теория возмущений или метод по-

следовательных приближений является одним из наиболее распространенных методов приближенного решения уравнения Шредингера. Этот метод приме-

ним тогда, когда гамильтониан можно представить в виде

название оператор возмущения.

В случае стационарной теории возмущений необходимо найти прибли-

причем предполагается, что решение уравнения Шредингера для невозмущен-

m

с неизвестными коэффициентами cm . Решение уравнения (5.2) ищут методом последовательных приближений. Для этого коэффициенты разложения и зна-

чения энергии записывают в виде

38

где cm( 1 ) , cm( 2 ) , … E( 1 ) , E( 2 ) , … – поправки первого, второго и т.д. порядков малости к коэффициентам разложения и уровням энергии.

Можно показать, что при отсутствии вырождения поправки к уровням

где штрих у суммы означает, что суммирование ведется по m ≠ n .

Примеры решения задач

Задача 5.1

Для частицы, находящейся в бесконечно глубокой потенциальной яме ширины l ( 0 < x < l ) , найти в первом порядке теории возмущений смещение энергетических уровней под действием возмущения вида

U ( x ) = U 0 (l − 2 x − l ), V0 > 0 (см. рис. 9). l

39

U ( x )

V 0

Рис. 9. Схематичное изображение возмущающего потенциала

Решение задачи

Согласно стационарной теории возмущений при отсутствии вырождения поправка первого порядка к энергии определяется соотношением

где Ψn( 0 )( r ) – волновая функция стационарных состояний невозмущенной сис-

темы;

При отсутствии возмущения рассматриваемая квантовомеханическая система представляет собой свободную частицу, находящуюся в бесконечно глубокой потенциальной яме ширины a ( 0 < x < a ) . Соответствующие волно-

вые функции стационарных состояний невозмущенной системы хорошо из-

вестны и имеют вид

Тогда смещение энергетических уровней в первом порядке теории воз-

мущений определяется соотношением

40

Разбивая промежуток интегрирования на две части, получим

Пользуясь формулой sin2 α = ( 1 − cos 2α ) / 2 и интегрируя, окончательно

найдем

Задачи для самостоятельного решения

5.2. Для частицы, находящейся в бесконечно глубокой потенциальной яме ширины l ( 0 < x < l ) , найти в первом порядке теории возмущений смеще-

ние энергетических уровней под действием возмущения вида (см. рис. 10).

U ( x )

V 0

Рис. 10. Схематичное изображение возмущающего потенциала