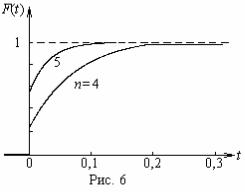
|
ì |
|
−10t |
,t > 0,n = 4; |
|
1 - 0,51e |
|
||
F(t)= |
ï1 - 0,24e−20t ,t > 0,n = 5; |
|||
|
í |
|
|
|
|
ï |
0, |
t £ 0,n = 4;5. |
|
|
î |
|||
Из этих графиков следует, что вероят- ность того, что время ожидания начала ремонта часов окажется меньшим, например 0,1 раб. дня, при n = 4 и п = 5 соответственно равна 0,81
и0,97.
2.4.Замкнутые системы массового обслуживания
До сих пор мы рассматривали только такие системы массового обслужи-
вания, для которых интенсивность l входящего потока требований не зависит от состояния системы. В этом случае источник требований находится вне сис- темы и генерирует неограниченный поток требований. В этом пункте рассмот- рим системы массового обслуживания, для которых l зависит от состояния системы, причем источник требований является «внутренним» и генерирует ог- раниченный поток требований.
Например, пусть в гараже имеется m автомашин и n(n<m) площадок для ремонта, причем на каждой площадке может находиться только одна автома- шина. Здесь автомашины являются источниками требований, а ремонтные площадки — обслуживающими приборами. Неисправная автомашина после об- служивания (ремонта) используется по своему прямому назначению и вновь становится потенциальным источником возникновения требований на обслу- живание. Ясно, что интенсивность поступления требований на обслуживание зависит от того, сколько автомашин в данный момент находится в эксплуата- ции и сколько автомашин обслуживается или стоит в очереди, ожидая обслу- живания.
Итак, рассмотрим систему массового обслуживания, состоящую из при- боров, каждый из которых может одновременно обслуживать только одно тре- бование, причем, как обычно, время обслуживания одного требования есть слу-
чайная величина с функцией распределения F(t)=1 - e−μt .
Входящий поток требований исходит из m(m>n) обслуживаемых объек- тов, которые в случайные моменты времени выходят из строя и требуют об- служивания. При этом каждый объект, находящийся в эксплуатации, генериру- ет независимо от других объектов пуассоновский поток требований с интен- сивностью l, так что если в эксплуатации находится k объектов, то общий (суммарный) входящий поток имеет интенсивность kl. Требование, поступив- шее в систему в момент, когда свободен хотя бы один прибор, немедленно идет на обслуживание. Если требование застает все приборы занятыми обслужива- нием других требований, то оно не покидает систему (как в случае систем с от- казами), а становится в очередь и ждет до тех пор, пока один из приборов не станет свободным (как в случае систем с ожиданием).
31
Системы массового обслуживания, в которых входящий поток требова- ний формируется из выходящего, называются замкнутыми.
Как и в п. 2.3, будем говорить, что система массового обслуживания на- ходится в состоянии k, если общее число требований, находящихся на обслу- живании и в очереди, равно k. Для рассматриваемой замкнутой системы, оче- видно, k = 0, 1, …, m. При этом если система находится в состоянии k, то число объектов, находящихся в эксплуатации, равно m - k. Заметим, что из этих и только этих m - k объектов формируется в данный момент времени входящий поток требований.
Составим систему дифференциальных уравнений для вероятности pk(t) того, что замкнутая система массового обслуживания в момент времени t нахо- дится в состоянии k = 0, l, ..., m. Для этой цели выпишем ряд элементарных, ра- нее уже неоднократно встречавшихся, формул.
Так как входящий поток требований по предположению является пуассо- новским с интенсивностью l, то вероятность того, что за время h в систему по- ступит k требований,
P (h)= |
(lh)k |
e−λh . |
(2.51) |
|
|||
k |
k! |
|
|
Отсюда непосредственно имеем: |
|
|
|
|
|
|
|
P (h)= e−λh =1 − λh + Ο(h), |
(2.52) |
||
0 |
|
|
|
P (h)= λhe−λh = λh + Ο(h). |
(2.53) |
||
1 |
|
|
|
Далее, так как время t обслуживания подчиняется показательному закону с параметром m, то
P(t < h)=1 - e−μh ; |
(2.54) |
P( τ > h ) = e−μh . |
(2.55) |
Далее применим стандартный классический метод, а именно в формуле
полной вероятности
m |
(t)pik |
(h) |
|
pk (t + h)= å pi |
(2.56) |
i=0
последовательно оценим переходные вероятности для различных возможных комбинаций индексов i и k, подставим эти оценки в формулу (2.56) и перейдем к пределу при h → 0 . В результате получим следующие четыре случая.
Случай 1
pkk |
(h) = íì1 - l(m - k )h - mkh + O(h),0 £ k < n; |
(2.57) |
|
1 - l(m - k )h - mnh + O(h),n £ k £ m. |
|
|
î |
|
Действительно, пусть система в момент времени t находится в состоянии k, 0 ≤ k < n. Тогда через время h она останется в том же состоянии k, если за это время не поступит в систему ни одно из m - k возможных требований (событие A1) и не покинут систему ни одно из k требований, находящихся там в момент времени t на обслуживании (событие A2). Но, используя теорему умножения ве- роятностей независимых событий и формулы (2.52) и (2.55), получаем:
P(A )= (e−λh )m−k |
, |
(2.58) |
1 |
|
|
32
|
|
|
P(A )= (e−μh )k , |
(2.59) |
|
|
|
|
2 |
|
|
и, следовательно, учитывая независимость событий A1 и A2, можно записать |
|||||
p |
kk |
(h)= P(A A )= P(A )P(A )= (e−λh )m−k (e−μh )k = |
|
||
|
1 2 |
1 |
2 |
|
|
= [1 - (m - k )lh + O(h)]× [1- mkh + O(h)]=1- (m - k )lh - mkh + O(h).
Случай, когда n £ k < m отличается от рассмотренного случая (0 £ k < n)
только тем, что при k > n обслуживаются не k, а только п требований (так как в системе имеется только п обслуживающих приборов, каждый из которых может обслуживать только одно требование).
Случай 2 |
(h)= íìμkh + Ο(h),0 < k < n; |
|
pk ,k −1 |
(2.60) |
|
|
îmnh + O(h),n £ k £ m. |
|
Действительно, система за время h перейдет из состояния |
k(0 < k < n) в |
|
состояние k - 1, если за это время не поступит в систему ни одно из m - k воз- можных требований (событие A1) и покинет систему (будучи обслуженным) только одно из каких-либо k обслуживаемых требований (событие A3). Но по
формуле Бернулли
|
P(A )= k(1- e−μh )(e−μh )k −1 |
= kmh + O(h). |
(2.61) |
|
3 |
|
|
Поэтому, учитывая независимость событий A1 и A3 и используя формулу |
|||
(2.58), запишем |
|
|
|
pk ,k −1 (h)= P(A1 A3 )= P(A1 )P(A3 )= kmh + O(h). |
|
||
Случай, когда |
n £ k £ m , отличается |
от рассмотренного |
случая |
(0 < k < n)только тем, |
что при k ³ n вероятность Р(А3) того, что освободится |
||
только один какой-либо из обслуживаемых приборов, не зависит от k, и, следо- вательно, вместо (2.61) имеет место равенство
P(A3 )= n(1 - e−μh )(e−μh )n−1 = nmh + O(h).
Случай 3
pk ,k +1 (h)= (m - k )lh + O(h),0 £ k < m. |
(2.62) |
Действительно, система за время h перейдет из состояния k(0 £ k < m) в состояние k +1, если за это время в систему поступит только одно из m - k воз- можных требований (событие А4) и систему не покинет ни одно из k требований (событие А2). Но, применяя теорему сложения вероятностей несовместных со- бытий и формулу (2.53), получаем
P(A4 )= (m - k)lhe−λh .
Поэтому, учитывая независимость событий А2 и А4 и используя (2.59), имеем:
pk ,k +1 (h)= P(A4 A2 )= P(A4 )P(A2 )=
= (m - k )lhe−λh (e−μh )k = (m - k)lh + O(h).
Случай 4
pik (h)= O(h), |
|
i - k |
|
³ 2. |
(2.63) |
|
|
33
Действительно, вероятность того, что за время h в систему поступят два или более требования, согласно (2.51) при k ³ 2 равна Ο(h). С другой стороны,
вероятность того, что за время h систему покинут два или более требования, со- гласно (2.54) и теореме умножения вероятностей независимых событий также равна Ο(h). Поэтому вероятность перехода системы из состояния i в состояние
k при |
|
i - k |
|
³ 2 за время h тем более равна Ο(h). |
||||
|
|
|||||||
Поставим теперь полученные оценки (2.57), (2.60), (2.62), (2.63) для pik(h) |
||||||||
в формулу (2.56). Тогда, например, при k = 0 получим |
||||||||
|
|
|
|
p0 (t + h)= p0 (t)p00 (h)+ p1 (t)p10 (h)+ Ο(h)= |
||||
|
|
|
|
= p0 (t)[1 − λh + Ο(h)]+ p1 (t)[μh + Ο(h)]+ Ο(h) |
||||
или |
|
|
|
|||||
|
|
|
|
|
p0 (t + h) - p0 |
(t) |
= -lmp0 (t) + O(h). |
|
|
|
|
|
|
h |
|
|
|
|
|
|
|
|
|
|
|
|
Переходя к пределу при h → 0, имеем |
|
|||||||
|
|
|
|
|
p0′ (t)= −λmp0 (t) + μp1 (t). |
|||
А так как нас будут интересовать только стационарные решения, то в послед-
нем равенстве переходим к пределу при t → ∞ : |
|
|
|
|
|||
|
0 = −λmp0 + μp1 . |
|
|
|
|
||
Проведя аналогичные рассуждения для k = 1,2,...,m , получим следую- |
|||||||
щую однородную систему алгебраических уравнений: |
|
|
|||||
ì |
|
|
0 = -amp0 + p1 ; |
|
|
|
|
ï |
0 = (m - k + 1)apk −1 - [(m - k)a + k]pk + |
||||||
ï |
|||||||
í |
|
+ (k + 1)pk +1 ; 0 < k < n; |
|
(2.64) |
|||
ï0 = (m - k + 1)ap |
k −1 |
- [(m - k )a + n]p |
k |
+ np |
k +1 |
,n £ k < m; |
|
ï |
|
|
|
|
|||
ï |
|
|
0 = apm−1 - npm . |
|
|
|
|
î |
|
|
|
|
|
|
|
Здесь
α = λ / μ, pk = lim pk (t),k = 0,1,...,m. |
|
||
|
t→∞ |
|
|
Для решения системы (2.64) введем новые переменные: |
|
||
zk = (m − k )αpk − (k + 1)pk +1 ,0 ≤ k < n; |
|
||
zk |
= (m − k)αpk |
− npk +1 ,n ≤ k ≤ m. |
(2.65) |
В новых переменных система (2.64), как легко проверить, принимает |
|||
очень простой вид: |
z0 |
= 0; |
|
|
|
||
|
zk −1 − zk = 0,0 < k < m; |
|
|
|
zm−1 = 0. |
zk = 0, |
|
Эта система имеет, |
очевидно, |
только нулевое решение |
|
k = 0,1,...,m −1 и, следовательно, равенства (2.65) можно переписать так: pk +1 = (mk−+k1)α pk ,0 £ k < n;
34
pk +1 = |
(m − k )α |
pk ,n £ k £ m. |
|
||||||
|
|
|
|
||||||
|
|
|
|
|
n |
|
|||
Отсюда последовательными подстановками легко находим |
|
||||||||
ì |
|
m!ak |
|
p0 ,1 £ k £ n; |
|
||||
ïï |
|
|
|||||||
k!(m - k )! |
(2.66) |
||||||||
pk = í |
|
m!ak |
|
|
|
|
|||
ï |
|
|
|
|
|
p0 ,n £ k £ m. |
|
||
ï |
|
k −n |
|
|
|
|
|
|
|
|
n!(m |
- k )! |
|
||||||
în |
|
|
|||||||
Величину же р0, как обычно, определяем из условия |
нормировки |
||||||||
m |
|
|
|
|
|
|
|
|
|
å pk = 1и полученных формул (2.66) для рk, k = 1,2,...,m . Зная вероятности рk, |
|||||||||
k =0 |
|
|
|
|
|
|
|
|
|
k = 1,2,...,m , можно вычислить среднюю длину очереди |
|
||||||||
|
|
|
|
|
|
m |
|
||
|
|
|
|
M1 = å(k - n)pk , |
(2.67) |
||||
|
|
|
|
|
|
k =n |
|
||
среднее число обслуживаемых и ожидающих обслуживания требований |
|||||||||
|
|
|
|
|
|
m |
|
||
|
|
|
|
M 2 |
|
= åkpk , |
(2.68) |
||
|
|
|
|
|
|
k =1 |
|
||
среднее число свободных от обслуживания приборов |
|
||||||||
|
|
|
|
|
|
n−1 |
|
||
|
|
|
|
M 3 |
|
= å(n - k )pk . |
(2.69) |
||
|
|
|
|
|
|
k =0 |
|
||
Отсюда легко находим коэффициент простоя обслуживаемого объекта |
|||||||||
|
|
|
|
ξ1 = M1 / m, |
(2.70) |
||||
коэффициент использования объектов |
|
||||||||
|
|
|
|
ξ2 = 1− (M 2 / m) |
(2.71) |
||||
и коэффициент простоя обслуживающих приборов |
|
||||||||
|
|
|
|
ξ3 = M 3 / n. |
(2.72) |
||||
Коэффициент x2 — весьма важная интегральная характеристика замкну- той системы массового обслуживания. Он характеризует интенсивность экс- плуатации объектов, так как практически равен вероятности того, что данный объект в любой момент времени t будет находиться в эксплуатации, т. е. рабо- тать. Для установившегося режима работы СМО его можно вычислить по фор-
муле
x2 |
= |
|
t1 |
|
, |
(2.73) |
|
t1 |
+ t |
2 |
|||||
|
|
|
|
где t1 = 1/ λ — среднее время безотказной работы объекта; t2 — среднее время простоя этого объекта.
Обозначим, как и в п. 2.3, время ожидания в очереди через q. Очевидно, общее время простоя П слагается из времени ожидания в очереди q и времени обслуживания τ, т. е. П = θ + τ. Переходя к математическим ожиданиям, учи- тывая равенства МП = t2 ; Mτ = 1/ μ и определяя t2 из формулы (2.73), находим
35
Mθ = MП − Mτ = t |
|
− |
1 |
= t |
|
1− ξ2 |
− |
1 |
= |
1 |
|
1− ξ2 |
− |
1 |
. |
(2.74) |
|
2 |
μ |
1 ξ2 |
μ |
λ |
ξ2 |
|
|||||||||||
|
|
|
|
|
|
μ |
|
||||||||||
Пример. Пусть для обслуживания (наладки) шести |
однотипных автоматов |
||||||||||||||||
выделено два мастера одинаковой производительности. Время от времени эти автоматы останавливаются и требуют наладки. Предполагается, что поток ос- тановок автоматов является пуассоновским, а время их наладки подчиняется показательному закону. Каждый автомат останавливается в среднем один раз в два часа, а среднее время наладки одного автомата одним мастером составляет
0,4 ч. Таким образом, λ = 0,5; μ = 2,5; α = λ/μ = 0,2.
Возможны следующие варианты организации обслуживания: 1) оба мас- тера обслуживают все шесть автоматов, так что при остановке автомата его об- служивает один из свободных мастеров; в этом случае n = 2 , m = 6 ; 2) каждый из двух мастеров обслуживает по три закрепленных за ним автомата. В этом случае n =1,m = 3 .
В результате вычислений по формулам (2.66) получаем табл.1 для перво-
го варианта и табл.2 |
для второго варианта. |
|
Т а б л и ц а 1 |
||
|
|
|
|
|
|
Число неработающих |
|
Число автоматов, |
|
Число свободных |
pk |
автоматов |
|
ожидающих наладки |
|
мастеров |
|
|
|
|
|||
0 |
|
0 |
|
2 |
0,320 |
1 |
|
0 |
|
1 |
0,384 |
2 |
|
0 |
|
0 |
0,192 |
3 |
|
1 |
|
0 |
0,077 |
4 |
|
2 |
|
0 |
0,023 |
5 |
|
3 |
|
0 |
0,005 |
6 |
|
4 |
|
0 |
0,000 |
|
|
|
|
|
Т а б л и ц а 2 |
Число неработающих |
|
Число автоматов, |
|
Число свободных |
pk |
автоматов |
|
ожидающих наладки |
|
мастеров |
|
|
|
|
|||
0 |
|
0 |
|
1 |
0,531 |
1 |
|
0 |
|
0 |
0,318 |
2 |
|
1 |
|
0 |
0,127 |
3 |
|
2 |
|
0 |
0,025 |
Используя значения pk в табл. 1 и 2, вычислим для обоих вариантов ко- эффициент простоя автоматов ξ1, коэффициент использования автоматов ξ2 и коэффициент простоя мастеров ξ3. Начнем с первого варианта. Среднее число автоматов, простаивающих в каждый момент в очереди из-за того, что мастера заняты наладкой других автоматов, определяется по формуле (2.67):
6
M1 = å(k − 2)pk = 0,140 .
k =2
Иными словами, в среднем из шести автоматов 0,14 автомата будет стоять в очереди до тех пор, пока не освободится мастер.
Для среднего числа неработающих автоматов, т. е. автоматов, которые налаживают и которые стоят в очереди, имеем согласно (2.68)
36