10)вероятность того, что число требований в очереди, ожидающих на-
∞
чала обслуживания, больше некоторого числа: P>m = åPk . Этот пока-
k =m+1
затель особенно необходим при оценке возможностей размещения требований при ограниченности времени для ожидания.
Кроме перечисленных критериев при оценке эффективности системы массового обслуживания могут быть использованы стоимостные показатели:
Cоб – стоимость обслуживания каждого требования в системе;
Сож – стоимость потерь, связанных с простаиванием требований в очере- ди в единицу времени;
Су – стоимость убытков, связанных с уходом из системы требований;
Сk – стоимость эксплуатации каждого прибора системы в единицу време-
ни;
Сnk – стоимость единицы времени простоя прибора системы.
Для выбора оптимальных параметров СМО по экономическим показате- лям можно использовать функцию стоимости потерь в системе:
∙ для системы с ожиданием
∙
ϕ(n)= (Cож M1 + Cnk M3 + Ck M4 )T ,
где T - интервал времени;
∙ для системы с отказами
ϕ∙ (n)= (Ck M 4 + Cу pnλ)T ;
∙ для смешанных систем массового обслуживания
∙
ϕ( n ) = ( Cnk M 3 + Cож M1 + Cу pnλ + Ck M 4 )T .
При решении некоторых задач целесообразно пользоваться критериями экономической эффективности системы массового обслуживания:
E = pобλСT − ϕ(n).
где С – экономический эффект, полученный при обслуживании каждого требо- вания; pоб - вероятность обслуживания требования.
2. ОСНОВНЫЕ ТИПЫ СИСТЕМ МАССОВОГО ОБСЛУЖИВАНИЯ
В разделе рассматриваются системы массового обслуживания в предпо- ложении пуассоновского входящего потока как времени обслуживания требо- ваний, так и других случайных факторов работы СМО. Такие системы массово- го обслуживания называют марковскими, поскольку процессы их функциони- рования являются марковскими случайными процессами с непрерывным вре- менем и дискретными состояниями. Для них хорошо разработан математиче- ский аппарат и получены аналитические решения.
15
2.1. Системы масового обслуживания с отказами
Пусть система массового обслуживания состоит из n однотипных обслу- живающих приборов и в эту систему поступает пуассоновский поток однород- ных требований с интенсивностью l. Предположим далее, что время обслужи- вания каждого требования каждым прибором подчиняется показательному за- кону с параметром m. Если оказывается, что все обслуживающие приборы заня- ты, то требование получает отказ и покидает систему необслуженным. Такие системы массового обслуживания называются системами с отказами (или сис- темами с потерями).
Прежде всего выведем систему дифференциальных уравнений для веро- ятности pk(t) того, что в системе в момент времени t находится на обслужива- нии k требований (k = 0, 1, ..., n). Сразу же заметим, что в любой момент време-
n
ни t должно выполняться условие нормировки å pk (t) = 1. Это непосредствен-
k =0
но следует из того, что в любой момент времени t в системе находится на об- служивании либо 0, либо 1, либо, наконец, n требований.
По формуле полной вероятности имеем
n |
(t)pik |
(h), |
|
pk (t + h) = å pi |
(2.1) |
i=0
где pik(h) — условная вероятность того, что через промежуток времени h будет обслуживаться k требований, если вначале обслуживалось i требований.
Будем считать h достаточно малым. Так как рассматриваемый поток тре-
бований — пуасcоновcкий и его плотность равна l, то можно написать: |
|
P³1 (h)= λh + Ο(h); |
(2.2) |
P³2 (h) = Ο(h), |
(2.3) |
где P³m(h) — вероятность того, что в течение промежутка времени h в систему на обслуживание поступит не менее m требований, Ο(h)- величина более высо-
кого порядка малости, чем h. Из формул (2.2) и (2.3) непосредственно следует, что вероятность поступления в течение промежутка времени h в систему точно одного требования равна lh+O(h).
Далее, используя функцию распределения F(t) = 1- e-mt времени обслу- живания t, подчиняющегося показательному закону с параметром m, для веро- ятности Р (t <h) того, что требование будет обслужено за время, меньшее h, на-
ходим
P(táh) =1 - e-mh = mh + O(h), |
(2.4) |
откуда |
|
P(tñh) = e-mh . |
(2.5) |
Правая часть соотношения (2.5) равна вероятности того, что время об- служивания превзойдет h, т. е. вероятности того, что ни один занятый прибор не освободится за время h. Следовательно, если на обслуживании находится k требований, то вероятность того, что ни один из k обслуживающих приборов не
16
освободится за время h, по теореме умножения вероятностей независимых со- бытий равна e-μkh. Поэтому для вероятности того, что за время h освободится хотя бы один из k приборов, получаем
1 - e−μkh = mkh + O(h).
А так как вероятность освобождения двух и более приборов за время h равна O(h), то вероятность освобождения за время h точно одного из k прибо-
ров равна
(2.6)
Найдем формулы для условных вероятностей pik(h). Пусть pik(h) = P(А), где событие А означает, что в системе через время h не будет ни одного требо- вания при условии, что в начальный момент в ней также не было требований. Очевидно, событие А можно представить в виде суммы несовместных событий:
A = A1 + A2 A3 + A4 A5 , |
(2.7) |
где А1 — за время h не поступило ни одного требования; А2 — за время h по- ступило одно требование; А3— это требование будет обслужено до окончания рассматриваемого промежутка времени h; А4 — за время h поступило более од- ного требования; А5 — эти требования будут обслужены до окончания рассмат- риваемого промежутка времени h.
Но из формул (2.2) — (2.4) следует:
P(A1 )= 1 - lh + O(h);
P(A2 ) = lh + O(h); P(A3 )= mh + O(h); P(A4 )= O(h); P(A5 ) = O(h);
Отсюда и из (2.7), используя теоремы сложения вероятностей несовмест- ных событий и умножения вероятностей независимых событий, находим
p00[ (h)= P(A()=)]P([A1 ) + P((A)2])P[(A3 ) + (P()A] 4 )P((A)5 )(= ) ( ) (2.8)
= 1 - lh + O h + lh + O h × mh + O h + O h O h =1 - lh + O h .
Таким образом, вероятность поступления в промежуток времени (t, t + h) m требований (m =1, 2, ...) и их обслуживания в этом же промежутке имеет бо- лее высокий порядок малости, чем h. По этой причине эту вероятностную ком- поненту мы далее явно выписывать не будем, считая ее содержащейся в симво-
ле O(h).
Пусть k - i ³ 2. Тогда pik(h) равна вероятности того, что в систему за время h поступит на обслуживание не менее двух требований, и, следовательно, по формуле (2.3) имеем
pik (h) = O(h),i £ k - 2. |
(2.9) |
Если же i - k ³ 2, то pik(h) равна вероятности того, что за время h систему покинут не менее двух обслуженных требований, и, следовательно, по формуле
(2.4) имеем
pik (h) = [mh + O(h)]i−k = O(h),i ³ k + 2 . |
(2.10) |
Величина pk,k+1(h) с точностью до O(h) равна вероятности того, что в сис- |
|
тему за время h поступит на обслуживание одно требование, т. е. |
|
pk ,k +1 (h) = lh + O(h),0 £ kán . |
(2.11) |
17
Аналогично величина pk,k-1(h) с точностью до O(h) равна вероятности то- го, что за время h освободится точно один прибор из k, и, следовательно, со- гласно (2.6)
pk ,k −1 (h)= μkh + Ο(h),0 < k ≤ n . |
(2.12) |
Если в системе в некоторый момент времени t находится на обслужива- нии k требований, то в момент t+h в этой системе может оказаться любое число требований от 0 до n и поэтому можно написать å pik (h) = 1.
i=0 |
|
Отсюда и из формул (2.9) и (2.10) имеем |
|
pkk (h)= 1 − pk ,k −1 (h) − pk ,k +1 (h)+ Ο(h),0 ≤ k ≤ n |
(2.13) |
или, принимая во внимание соотношения (2.11) и (2.12), получим |
|
pkk (h)= 1 − λh − μkh + Ο(h),1 ≤ k ≤ n − 1. |
(2.14) |
Наконец, учитывая, что pn,n+1(h)=0 (в системе не может находиться n+1 требований, так как рассматривается система с отказами и в ней имеется только
n приборов), из соотношений (2.13) и (2.12) получаем |
|
|
|
|
pnn (h) = 1 − μkh + Ο(h). |
|
(2.15) |
Подставим теперь оценки (2.8) — (2.15) для pik(h) |
в формулу (2.1). В ре- |
||
зультате получим: |
|
|
|
ì p0 (t + h)= p0 (t)(1- lh)+ p1 (t)mh + O(h); |
|
||
ïï pk (t + h)= pk−1 (t)lh + pk (t)(1 - lh - mkh)+ |
(2.16) |
||
í |
+ pk+1 (t)m(k + 1)h + O(h),1£ k £ n |
-1; |
|
ï |
|
||
îï pn |
(t + h)= pn−1 (t)lh + pn (t)(1 - mnh)+ O(h). |
|
|
Здесь в каждом уравнении все члены, содержащие множителем величи- ну O(h) объединены вместе и обозначены тем же символом O(h).
Запишем систему (2.16) в виде
ì |
|
|
p |
0 |
(t + h)- p |
0 |
(t) |
= -lp0 (t)+ mp1 (t)+ O(1); |
|
||||||||
ï |
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
ï p (t + h)h- p (t) |
= lpk −1 (t)- (l + km)pk (t)+ |
|
|||||||||||||||
ï |
|
k |
|
|
k |
|
|
|
|
|
(2.17) |
||||||
|
|
|
|
|
|
|
|
|
|
||||||||
í |
|
|
|
|
|
|
h |
|
|
|
|
|
|
|
|
|
|
ï |
|
|
|
|
|
|
+ m(k + 1)pk +1 (t)+ O(1),1£ k £ n -1; |
|
|||||||||
ï p |
n |
(t + h)- p |
n |
(t) |
|
= lpn−1 (t)- mnpn (t)+ O(1), |
|
||||||||||
ï |
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
h |
|
|
|
|
|
|
|
|||||
î |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
где символ O(1) означает величину, стремящуюся к нулю при h ®0.
Система разностных уравнений (2.17) в пределе при h ®0 превращается в
систему дифференциальных уравнений: |
|
|
|
ì |
p0¢ (t)= -lp0 (t)+ mp1 (t); |
|
|
ïï pk¢ (t)= lpk −1 (t)- (l + km)pk (t)+ |
(2.18) |
||
í |
+ m(k +1)pk +1 (t),1£ k £ n - |
1; |
|
ï |
|
||
ï |
¢ |
|
|
î |
pn (t)= lpn−1 (t)- mnpn (t). |
|
|
Если предположить, что в начальный момент t=0 в системе нет требова- ний, то получим начальные условия:
18
p0 (0) = 1; p1 (0) = 0;...; pn (0) = 0. |
(2.19) |
Хотя система обыкновенных дифференциальных уравнений (2.18) с на- чальными условиями (2.19) и является линейной, причем с постоянными коэф- фициентами, найти ее точное, т.е. аналитическое, решение в явном виде при m>2 в общем случае невозможно. Конечно, при желании систему (2.18), (2.19) всегда можно решить с любой степенью точности численно, например методом Рунге - Кутта. Однако численное решение с точки зрения качественного анали- за представляет известные неудобства. Вместе с тем качественное исследование решений систем дифференциальных уравнений, возникающих в теории массо- вого обслуживания, весьма желательно.
Рассмотрим более подробно частный случай системы (2.18), (2.19) при
n=2, m=l, l=2. В этом случае система (2.18) принимает вид: |
|
|
ì |
p0′ = -2 p0 + p1; |
|
ï |
|
(2.20) |
í p1¢ = 2 p0 - 3p1 + 2 p2 ; |
||
ï |
¢ |
|
î |
p2 = 2 p1 - 2 p2 . |
|
Используя равенство p2 (t) = 1− p0 (t)− p1 (t), исключим из второго урав-
нения системы (3.20) функцию р2(t). Тогда, отбрасывая третье уравнение, полу- чим:
ì p0¢ = -2 p0 + p1; íî p1¢ = -5 p1 + 2.
Решение этой системы, как легко проверить, имеет вид:
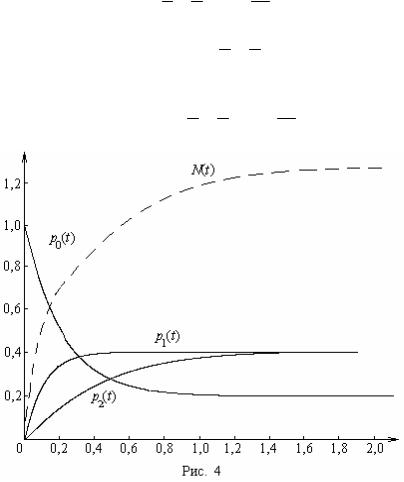
p0 (t)= 15 + 23 e−2t + 152 e−5t ; p1 (t) = 52 - 52 e−5t .
Кроме того,
p2 (t) = 25 - 23 e−2t + 154 e−5t .
19
На рис. 4 функция N (t) = p1 (t)+ 2 p2 (t) равна среднему числу занятых об-
служивающих приборов. Из рис. 4 видно, что в рассматриваемом случае, начи- ная с момента t =1,5, практически устанавливается стационарный режим, опре-
деляемый по формулам |
|
|
|
|
|
p0 |
= lim p0 |
(t)= 0,2; p1 |
= lim p1 (t)= 0,4; |
(2.21) |
|
|
t→∞ |
|
|
t→∞ |
|
|
|
p2 |
= lim p2 (t) = 0,4. |
|
|
|
|
|
t→∞ |
|
|
Решение (2.21) называется стационарным решением системы (2.20). Оно соответствует так называемому состоянию равновесия, характеризуемому по- стоянством во времени всех вероятностных показателей системы массового об- служивания. При этом, что весьма примечательно, это решение не зависит от исходного распределения вероятностей числа требований в системе, т.е. от ве- личин р0(0), p1(0), p2(0). Этот факт имеет для теории массового обслуживания неоценимое значение.
Как уже отмечалось, найти явное аналитическое решение системы (2.18) при произвольном n в общем случае невозможно. Однако стационарное реше- ние этой системы, если оно существует, найти легко. Действительно, полагая
lim pk (t)= pk ,k = 0,1,...,n
t→∞
и переходя к пределу в дифференциальной системе (2.18) при t → ∞ , получим уже алгебраическую систему:
ì |
|
|
|
|
|
|
0 = -lp0 + mp1; |
|
|
|
|
|
||||||
ï |
= lpk −1 - (l + km)pk |
+ m(k +1)pk +1 ,1£ k £ n -1; |
(2.22) |
|||||||||||||||
í0 |
||||||||||||||||||
ï |
|
|
|
|
|
0 = lpn−1 - mnpn . |
|
|
|
|
||||||||
î |
|
|
|
|
|
|
|
|
|
|||||||||
Для упрощения записи системы (2.22) разделим каждое ее уравнение на |
||||||||||||||||||
μ, и введем обозначение a=l/m. В результате будем иметь: |
|
|||||||||||||||||
ì |
|
|
|
|
|
0 = -ap0 + p1; |
|
|
|
|
|
|
||||||
ï |
= apk −1 - (a + k )pk |
+ (k +1)pk+1 ,1£ k £ n -1; |
(2.23) |
|||||||||||||||
í0 |
||||||||||||||||||
ï |
|
|
|
|
|
0 = apn−1 - npn . |
|
|
|
|
|
|||||||
î |
|
|
|
|
|
|
|
|
|
|
||||||||
Предположим, что р0 известно. Тогда, используя последовательно урав- |
||||||||||||||||||
нения системы (2.23), получим: |
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
ì |
|
|
|
|
p1 = ap0 ; |
|
|
|
|
|
|
|
|
||||
|
ï |
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
ï |
|
|
1 |
|
|
|
|
|
|
|
a |
2 |
p |
|
|
|
|
|
ï |
|
|
[- ap0 + (a +1)p1 ]= |
|
0 |
|
|
||||||||||
|
í p2 |
= |
|
|
|
|
|
; |
|
|||||||||
|
2 |
|
2 |
|
|
|||||||||||||
|
ï |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
ï p |
|
= |
1 |
[- ap + (a + 2)p |
|
]= a3 p0 |
|
||||||||||
|
2 |
|
2 |
|
||||||||||||||
|
ï |
|
3 |
1 |
|
|
|
|
|
|
3! |
|
|
|
||||
|
î |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
и вообще для любого k ≤ n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
pk = |
|
ak p |
0 |
. |
|
|
|
|
|
|
|
(2.24) |
|
|
|
|
|
|
|
k! |
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Чтобы избавиться в формуле (2.24) от р0, а заодно и определить р0, ис-
пользуем условие нормировки
20
n
å pk = 1,
k =0
справедливое также и при t → ∞ . Подставляя в это условие вместо рk правую часть равенства (2.24), получаем
|
|
|
n |
k |
|
|
|
|
|
p0 åα |
|
= 1, |
|
||||||
откуда |
|
k =0 k! |
|
|
|
|
|||
|
|
1 |
|
|
|
|
|||
p0 |
= |
|
. |
(2.25) |
|||||
|
n |
|
k |
||||||
|
|
|
|
å α |
|
|
|
|
|
|
|
|
|
k =0 |
k! |
|
|
|
|
Наконец, из формул (2.24) и (2.25) окончательно находим |
|
||||||||
|
|
|
|
αk |
|
|
|
|
|
p |
k |
= |
|
k! |
|
|
,k = 0,1,...,n. |
(2.26) |
|
|
|
k |
|
||||||
|
|
|
n |
α |
|
|
|
||
|
|
|
å |
|
|
|
|
||
|
|
|
|
k =0 |
k! |
|
|
|
|
Формулы (2.26) называются формулами Эрланга. Они дают явное анали- тическое решение для стационарного распределения вероятностей числа требо- ваний, находящихся на обслуживании в системе с отказами.
Заметим, что прямой путь получения стационарного решения из неста- ционарного при t → ∞ (как это было сделано для случая n=2, μ=l, λ=2) практи- чески исключается из-за технических трудностей, возникающих при нахожде- нии нестационарного решения системы (2.18) в явном виде. Вместе с тем на практике обычно интересуются именно установившимися во времени (т. е. ста- ционарными) вероятностными характеристиками функционирования системы массового обслуживания.
Для рассматриваемой системы с отказами наибольший интерес представ- ляет вероятность отказа, т. е. вероятность того, что в момент поступления оче- редного требования на обслуживание все приборы будут заняты:
|
|
|
|
|
αn |
|
|
|
|
αn |
|
|
|
||
p |
отк |
= p |
n |
= |
n! |
|
= p |
0 |
, |
|
|
||||
|
k |
n! |
|
||||||||||||
|
|
|
n |
|
|
|
|
|
|
||||||
|
|
|
|
|
åα |
|
|
|
|
|
|
|
|||
|
|
|
|
|
k=0 |
k! |
|
|
|
|
|
|
|
|
|
и среднее число приборов, занятых обслуживанием: |
|
||||||||||||||
|
|
n |
|
|
|
|
|
n |
|
α |
k |
|
|
= α(1 − pn ). |
|
M 4 = åkpk = p0 |
å |
|
|
|
|
|
|||||||||
|
|
|
|
|
|
||||||||||
|
|
k =1 |
|
|
|
|
k =1 (k − 1)! |
|
|||||||
(2.27)
(2.28)
Первая величина рn характеризует полноту обслуживания входящего по- тока, вторая величина M4— степень загрузки системы массового обслуживания.
Пример. Автоматическая телефонная станция (АТС) имеет пять линий связи (пять обслуживающих приборов). Очевидно, что моменты поступления на АТС требований, т. е. заявок на соединение с абонентом для ведения разго- воров, равно как и продолжительность этих разговоров, являются случайными.
21