1.2. Пуассоновский поток требований
Обозначим через X(t) число требований, поступающих в систему массо- вого обслуживания за промежуток времени (0, t). Если требования поступают на обслуживание в случайные моменты времени, то X(t) —случайная функция,
одна из возможных реализаций которой показана на рис. 2.
Функция X(t), очевидно, принимает только целые неотрицательные значения и является не- убывающей при возрастании времени t. Она опре-
деляет некоторую временную последовательность событий, или, как принято говорить в теории мас- сового обслуживания, поток требований.
Далее, если не оговорено противное, пред- полагается, что входящий поток требований обладает следующими тремя свой- ствами:
1) вероятность поступления k требований в промежутке времени (0, t) равна вероятности поступления k требований в любом другом промежутке вре- мени (α, α+t) той же продолжительности. Это свойство потока называется ста- ционарностью. Оно выражает неизменность вероятностного режима потока во времени;
2)вероятность поступления k требований в систему после произвольного
момента времени t0 не зависит от того, когда и сколько поступило требований до этого момента времени. Такое свойство потока называется «отсутствием по- следействия». Из него следует взаимная независимость поступления того или
иного числа требований на обслуживание в непересекающиеся промежутки времени;
3)вероятность поступления более одного требования за малый промежу-
ток времени t есть величина более высокого порядка малости, чем t. Это свойство потока называется ординарностью. Оно выражает практическую не- возможность одновременного поступления двух или более требований.
Поток требований, удовлетворяющий двум последним перечисленным свойствам (стационарность, отсутствие последействия, ординарность), называ- ется пуассоновским. Если поток обладает всеми тремя свойствами, то он назы- вается простейшим.
Обозначим через Pk(t) вероятность поступления в систему массового об- служивания ровно k требований за промежуток времени t, т. е. поло- жим Pk (t) = P(X (t) = k ). Если λ — плотность (интенсивность) потoка требова-
ний, т. е. среднее число требований, поступающих на обслуживание в единицу времени, то для пуассоновского потока при малом h можно написать:
Pk (h) ≈ 0, k=2, 3, ...; P1 (h)≈ λh, P0 (h)≈1 − λh.
Отсюда, воспользовавшись теоремой умножения вероятностей независи- мых событий, получим:
P0 (t + h) = P0 (t)P0 (h) ≈ P0 (t)(1 − λh);
9
Pk (t + h) = Pk (t)P0 (h)+ Pk −1 (t)P1 (h)+
+ Pk −2 (t)P2 (h)+ ... » Pk (t)(1- lh)+ Pk −1 (t)lh,k ³ 1
или |
(t + h)- P0 (t) |
|
|
|
|
|||||
|
|
P0 |
» -lP0 |
(t); |
|
|
||||
|
|
|
h |
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
||
|
Pk (t + h)- Pk (t) |
» -lPk |
(t)+ lPk −1 (t),k |
³ 1. |
|
|||||
|
h |
|
|
|
||||||
|
|
|
|
|
|
|
|
|
||
Переходя к пределу при h ®0, получаем: |
|
|
|
|||||||
|
|
|
P0′(t)= -lP0 (t); |
|
|
(1.3) |
||||
|
|
Pk′(t)= -lPk (t)+ lPk −1 (t), k ³1. |
(1.4) |
|||||||
Допустим, что к начальному моменту t=0 не поступило ни одного требо- вания, т. е.
P0 (0)=1, Pk (0)= 0, k =1, 2, ...
Тогда решение системы дифференциальных уравнений (1.3), (1.4) можно
записать в виде
|
P (t)= e−λt ; |
|
|
|
(1.5) |
||||||
|
0 |
|
|
|
|
|
|
|
|
|
|
Pk (t) = le−λt |
òt |
eλt Pk −1 (t)dt. |
(1.6) |
||||||||
|
|
|
|
0 |
|
|
|
|
|
|
|
Решая рекуррентное соотношение (1.6) последовательно для k=1,2, ... и |
|||||||||||
учитывая при этом (1.5), находим: |
|
|
|
|
|
|
|
|
|
|
|
|
P (t)= λte−λt ; |
|
|
|
|
|
|||||
|
1 |
|
|
|
|
|
|
|
|
|
|
P (t)= (lt)2 e−λt |
; |
|
|
|
|
||||||
|
2 |
|
|
|
2! |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
. . . . . . . . . . . |
|
|
|
|
|||||||
|
P (t) = (lt)k e−λt . |
|
(1.7) |
||||||||
|
k |
|
|
|
k! |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
По определению математического ожидания из (1.7) |
|
|
|||||||||
∞ |
|
|
|
|
∞ |
|
k |
e |
−λt |
||
MX (t)= åkPk (t) |
= åk |
(lt) |
|
|
= |
||||||
|
|
|
|
||||||||
k =1 |
|
|
|
k =1 |
k! |
|
|
||||
∞ |
(lt) |
k −1 |
|
|
|
|
|
|
|
|
|
= lte−λt å |
|
|
= lt, |
|
|
|
|
|
|||
(k - 1)! |
|
|
|
|
|
||||||
k =1 |
|
|
|
|
|
|
|
|
|||
т. е. среднее число требований, поступающих на обслуживание за время t, рав- но lt.
Формула (1.7) дает распределение вероятностей числа требований, посту- пающих на обслуживание за данный промежуток времени t. Вместо этого мож-
но пользоваться распределением вероятностей промежутка времени Т между двумя последовательными моментами поступления требований. Это распреде- ление получается автоматически из формулы (1.7) при k=0. В самом деле, вели- чина P0(t) по определению равна вероятности P(T>t) того, что случайная вели- чина Т превзойдет t, поэтому можно написать
10
F(t) = P(T < t) = 1- P(T > t) = 1- e−λt . |
(1.8) |
Отсюда для соответствующей плотности вероятностей имеем
′ |
−λt |
, |
(1.9) |
f (t) = F (t) = λe |
|
т.е. длительность интервала времени между двумя последовательными момен- тами поступлений требований пуассоновского потока имеет показательное рас- пределение. При этом
∞ |
|
|
|
1 |
|
|
|
MT = òtle−λt dt = |
; |
|
|
||||
l |
|
|
|||||
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
∞ æ |
1 ö |
2 |
|
|
1 |
|
|
DT = òçt - |
|
÷ |
le−λt dt = |
|
. |
||
|
2 |
||||||
0 è |
l ø |
|
|
|
l |
||
Таким образом, математическое ожидание промежутка времени между
двумя последовательными моментами поступлений требований равно обратной величине интенсивности потока требований. Этого и следовало ожидать, так как ясно, что средняя продолжительность времени между двумя последова- тельными моментами поступления требований должна быть равна обратной ве- личине от среднего числа требований, поступающих в единицу времени.
Формулы (1.8) и (1.9) дают закон распределения вероятностей для интер- вала времени не только между двумя последовательными моментами поступле- ния требований, но и между произвольным фиксированным моментом времени и ближайшим моментом поступления требования. Действительно, если Т - ин- тервал времени между двумя последовательными моментами поступления тре- бований, а t - интервал времени после поступления последнего требования в систему, то для функции распределения F1(t) оставшегося интервала времени T − τ в силу (1.8) имеем
F (t)= P(T - t < t |T > t)= |
P(T − τ < t,T > τ) |
= |
||||||||
|
|
|||||||||
1 |
|
|
|
|
|
|
P(T > t) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= |
P(τ < T < τ + t) |
= F(τ + t)− F(τ) |
= |
|
||||||
|
|
P(T > t) |
|
|
|
1- F(t) |
|
|
|
|
|
= |
e−λt - e−λ(t+τ) |
|
= 1- e−λt = F(t), |
|
|
||||
|
e−λτ |
|
|
|||||||
|
|
|
|
|
|
|
|
|||
следовательно, функция распределения оставшегося интервала времени Т-t совпадает с функцией распределения всего интервала времени Т.
Таким образом, для пуассоновекого потока можно утверждать, что закон распределения интервала времени от произвольного момента t0 до момента по- ступления ближайшего требования в систему массового обслуживания не зави- сит от того, поступило или нет требование в момент t0 .Это свойство следует из свойства отсутствия последействия, являющегося основным для пуассоновско-
го потока
1.3. Типы систем обслуживания. Краткая символика
Существуют следующие типы систем массового обслуживания.
11
Системы с отказами (потерями) – требования, которые при поступлении не находят ни одного свободного прибора, теряются.
Системы с ожиданием – возможно ожидание для любого числа требова- ний, которые не могут быть обслужены сразу.
Комбинированные системы с ожиданием и потерями (системы ожидания с ограничениями). Например, ожидать может только конечное число требова- ний, определяемое конечным числом мест ожидания. Требование может те- ряться и тогда, когда время ожидания или пребывания в системе превышает за- данные границы.
Приоритетные системы – поступающие требования имеют различные личные приоритеты.
Многофазные системы – обслуживание состоит из нескольких последова- тельных этапов или “фаз”.
Другой важный класс систем – так называемые замкнутые СМО. В отли- чие от незамкнутых (говорят “открытых”) систем массового обслуживания в замкнутых системах входящий поток требований формируется из выходящего. К таким системам относятся и так называемые сети массового обслуживания.
Сеть массового обслуживания представляет собой совокупность конечно- го числа М обслуживающих центров, в которых циркулируют сообщения, пе- реходящие в соответствии с маршрутной матрицей из одного центра в другой. Под центром обслуживания понимают систему массового обслуживания, со- стоящую из А одинаковых приборов (1 ≤ A ≤ ∞ ) и буфера объемом С (0 ≤ C ≤ ∞). При A = 1 центр называется однолинейным, при A = ∞ - бесконеч- нолинейным.
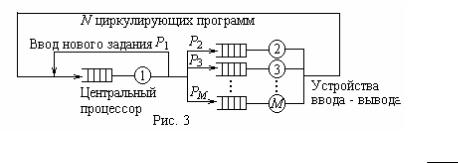
Рассмотрим пример сети массового обслуживания, являющейся простей- шей моделью мультипрограммной ЭВМ (рис.3).
Конечное число N программ (сообщений), соответствующих уровню мультипрограммирования, в соответствии с вероятностями Pi (i =1, M ) пооче-
редно обращается к одному из M центров обслуживания.
Обслуживающий центр 1 моделирует работу центрального процессора, а центры 2, 3, …, М представляют группу внешних запоминающих устройств.
Для краткой характеристики систем массового обслуживания Кендалл впервые ввел символику, которая оправдала себя. Изложим ее в несколько рас- ширенном виде.
Символика использует пять разрядов: первый разряд для характеристики входящего потока однородных событий, второй разряд для характеристики об- служивания, третий разряд определяет особенности структуры системы, в чет- вертом разряде фиксируются особенности очереди, пятый разряд вводится для
12