онные движения в гироинтеграторах с облегченными роторами могут оказаться существенными и заметно повлиять на его точность работы.

3. Двухстепенные гироскопы

3.1. Гиротахометры

Гиротахометрами называются двухстепенные гироскопы, предназначенные для измерения угловых скоростей объектов, таких как самолеты, суда, наземные транспортные средства и т. д. Широко используются гиротахометры также и в составе сложных многогироскопных систем.

Гиротахометры называют также и датчиками угловой скорости (ДУС), а также дифференцирующими гироскопами.

3.1.1. Гиротахометр с механической пружиной.

Схема прибора представлена на рис.32. Он состоит из гироузла 1 с гиромотором, центрирующих пружин 3, поршня демпфера 4, цилиндра демпфера 5, микрометрического винта 6 регулировки коэффициента демпфирования, шкалы 7, связанной с основанием 2, рычага 8, через который осуществляется центрирование гироузла и стрелки 9. Система координат 0XрYрZр связана с гироузлом, а система координат 0X0Y0Z0 – с основанием. Прибор является двухстепенным, т.к. его ротор имеет две угловых степени свободы: возможность вращения в подшипниках гироузла вокруг оси 0Xр и вместе с гироузлом вокруг оси 0Yр.

72

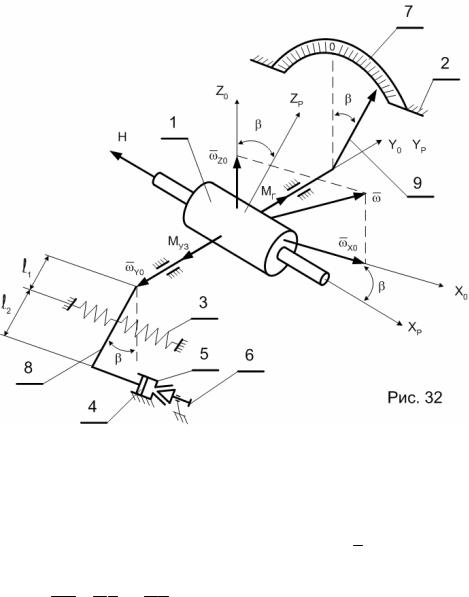
В исходном положении, в случае неподвижного основания, центрирующие пружины удерживают гироузел в таком положении, что оси системы координат 0XрYрZр совмещаются с осями соответствующими осям системы координат 0X0Y0Z0, связанной с основанием, а стрелка 9 находится на нулевой отметке шкалы.

Положим теперь, что основание поворачивается с некоторой угловой скоростью, проекции которой на оси 0X0 и 0Z0 соответственно равны ωX0

и ωZ0 . Как известно, воздействие на прибор угловой скорости ω, вектор

которой лежит в плоскости 0X0Z0, приводит к появлению гироскопическо-

го момента МГ = Hωsin(Hω) .

73

Вектор МГ направлен по оси 0Y0 в положительном направлении, т.к.

гироскопический момент стремится совместить вектор H с вектором ω по кратчайшему пути. В результате происходит поворот гироузла вокруг оси 0Yр на некоторый угол .

С учетом факта конечности гироскопические моменты, обусловленные воздействием на прибор составляющих ωXo и ωZo вектора угловой

скорости ω, определяются простыми соотношениями:

МГ = МГ1 + МГ2 = H(ωx0 sinβ+ ωz0 cosβ) . Поворот гироузла под действием МГ вокруг оси 0Yр сопровождается появлением моментов сил сопротивления: момента инерционных сил Ми; момента сил сопротивления пружин Мпр; момента сил сопротивления в демпфере Мд и момента

••

сил трения МтрY. Момент инерционных сил МИ = Iy β, где Iy – момент

••

инерции гироузла относительно оси Y и β– угловое ускорение движения

циент жесткости пружин; l1 - плечо, образованное участком рычага между осью 0Yр и точкой крепления центрирующих пружин; - угол

где l2 - плечо, образованное участком рычага между осью 0Yр и точкой крепления поршня демпфера; kД - коэффициент пропорциональности между скоростью перемещения поршня относительно стенок цилиндра и силой сопротивления движению поршня; VП- скорость перемещения

74

поршня относительно стенок цилиндра, равная VП = l β& при малых

скоростях поворота гироузла β& .

В каждый момент движения имеет место равенство моментов сил

лученное уравнение полностью определяет прибор как в части его характеристик, так и в части ошибок.

Идеальная характеристика прибора получается в статическом режиме

• ••

работы, т.е. при β = 0 и β = 0 , при условии Мтру =0 и β ≈ 0 .

Тогда kПрl21β = Hωz0 и β = (H / kПpl12 )ωz0 = kГТwz0 , где kГТ – коэффициент передачи гиротахометра. Таким образом, данный прибор измеряет угловые скорости поворота основания вокруг оси чувствительности, т.е.

вокруг оси

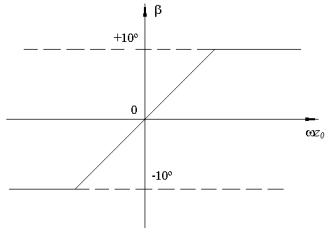
перпендикулярной плоскости, образованной главной осью гироскопа и осью подвеса рамки. Статическая характеристика идеализированного прибора представлена на рис.33.

Из соображений минимизации кинематических ошибок величина рабочего угла ограничивается 100.

Кинематическая ошибка прибора обусловлена конечностью рабо-

чего угла . Это обстоятельство приводит к следующему. Во-первых,

Рис.33

75

прибор начинает измерять не величину ωZ0 , а ее проекцию на ось чувст-

вительности прибора, т.е. ωZ0Y = ωZ0 cosβ. Во-вторых, он становится чувствительным к движению основания вокруг второй оси, - оси 0Xр, т.е. к угловой скорости ωX0 . Кинематическая ошибка легко находится из пол-

лишь в случае грубых измерений. В точных приборах это недопустимо, поэтому рабочее значение ограничивается диапазоном =20-50 ,что в свою очередь нежелательно, так как уменьшает крутизну выходного сигнала.

Статические ошибки прибора обусловливаются трением в подвесе по оси прецессии, т.е. по оси 0Yр. Они определяются из условия

•••

β= 0 ;β = 0;β- мал; cosβ =1; sinβ = 0. Тогда β = kГТMТРY / H.

Соответствующая характеристика прибора представлена на рис.34.

76

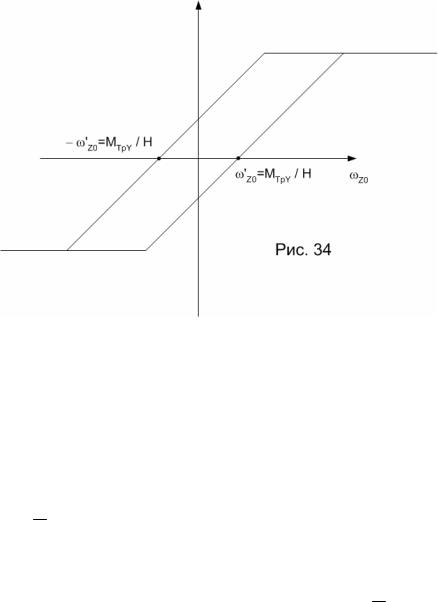
Таким образом наличие трения приводит к гистерезису статической характеристики прибора. При этом его пороговая чувствительность

ωz/0 = MТРУ / H становится конечной. Ее величина определяется, в

частности, моментом трения Мтру. Как известно Мтру зависит от давления на опоры по оси подвеса. Оно определяется не только силой веса гироузла. Существенное увеличение давления происходит также из-за гироскопических моментов. Так поворот основания как вокруг оси чувствительности, так и вокруг перпендикулярной ей оси приводит к дополнительному давлению со стороны гироузла на опоры в силу тенденции

вектора Н сохранить свое положение в пространстве неизменным. Это увеличение давления зависит от скорости поворота основания и может стать очень большим при значительных скоростях.

Аналогично проявляет себя и скорость поворота основания вокруг оси 0Yр. В самом деле в первый момент этого движения имеет место поворот

основания при неподвижном гироузле в силу тенденции вектора Н остаться неподвижным относительно абсолютного пространства. Тем самым

77

это движение в начальный момент обусловит появление выходного сигнала- смещение стрелки относительно нуля шкалы даже при ωz0 = 0. Да-

лее, в силу упомянутого процесса, происходит деформация пружин. Они создают момент внешних сил Mу, прикладываемый к гироузлу. Следствием этого является тенденция гироскопа прецессировать вокруг оси 0Z0 в

сторону совмещения Н и Му по кратчайшему пути. Это прецессионное движение невозможно из-за крепления оси рамки в подшипниках основания по оси 0Yр. Подшипники дополнительно нагружаются, что объясняется тенденцией гироскопа повернуться вокруг оси 0Z0. Основание развивает, в свою очередь, момент сил реакции, прикладываемый к гироузлу и действующий вокруг оси Z. Под действием этого момента сил реакции происходит прецессия гироскопа вокруг оси 0Yр в сторону обнуления My. Прецессия прекратится после поворота гироузла вокруг оси 0Yр на угол, равный углу поворота основания. Таким образом движение основания вокруг оси 0Yр также сопровождается дополнительным нагружением опор.

Следовательно, движение основания вокруг всех трех осей приводит к дополнительному нагружению подшипников, а, следовательно, и к увеличению трения по оси 0Yр. Результатом является увеличение статических ошибок. Увеличиваются при этом и кинематические ошибки.

Динамические ошибки прибора определяются из основного уравнения движения при условии малости и Мтр=0. Тогда cosβ =1, sin α = 0 и уравнение движения прибора имеет следующий вид:

Таким образом гиротахометр представляет собой звено второго порядка. При этом, в силу возможности регулировать микрометрическим винтом, можно сделать таким, что корни характеристического уравнения станут:

-действительными и отрицательными при >1;

-действительными и кратными при =1;

-комплексными при <1.

В первом случае, >1, гироскоп становится апериодическим звеном второго порядка со сравнительно малым быстродействием. Во втором случае, =1, гироскоп также остается апериодическим звеном второго порядка при максимальном быстродействии и отсутствии колебательности в переходном процессе. В третьем случае, <1,повышается быстродействие прибора при увеличении колебательности.

Проведенный анализ свободного движения гироскопа позволяет оценить его динамические ошибки. Как известно, для любого летательного аппарата, судна, наземного транспортного средства и т.д. характерно колебательное движение вокруг, в общем случае, всех трех его осей. Тем самым, например, в нашем случае можно считать, что основание движется

вокруг оси 0Z0 по гармоническому закону ψz0 = ψz m sinνt с частотой

.

Отсюда угловая скорость движения основания

ψ&.z0 = ψzm νcosνt = ωzm cosνt , где ωzm = ψzν – амплитуда угловой скорости.

Из передаточной функции прибора легко может быть найдено выражение для коэффициента передачи гиротахометра, как функция частоты колебаний основания :

kгт (ν) = kгт (0) / (1− ν2T2 )2 + 4ξ2ν2T2 . Обозначим , q

где q – относительная частота, поскольку 1/T– собственная частота колебаний гиротахометра. Тогда kгт (q) = kгт (0) / (1− q2 )2 + 4ξ2q2 .

Зависимость kгт(q, ) представлена на рис.35. Анализ семейства характеристик показывает, что k(q, ) ≈ const в диапазоне относительных частот q=0 – 0,2. Это значит, что гиротахометр измеряет угловые скорости движения оснований практически без ошибки, если частота колебаний основания в 5 – 10 раз меньше собственной частоты колебаний прибора. При этом большее постоянство k(q, ) достигается при .

Помимо амплитудных гиротахометру присущи и фазовые ошибки. Зависимость фазового сдвига, вносимого прибором, определяется простым

79