Для рассмотренного выше примера найдем передаточную функцию замкнутой системы по ошибке от задающего воздействия:

Лекция 12. Особенности построения математических моделей компьютерных систем управления. Методы линеаризации

В системах компьютерного управления, или цифровых автоматических системах (ЦАС), кроме квантования по времени выполняется квантование сиг- нала по уровню. Таким образом, ЦАС являются нелинейными импульсными системами. Достаточно точный анализ процессов в таких системах может быть выполнен только путем имитационного моделирования. Однако для проекти- руемой системы такое моделирование невозможно без предварительного ана- литического исследования. На основе достаточно простых аналитических ме- тодов должны быть определены структура системы, ее основные параметры и показатели качества, выбраны элементы системы.

Рассмотренные выше методы учета квантования по времени в рамках теории импульсных систем могут применяться для ЦАС, если характерный для

них эффект квантования по уровню удается учесть в рамках линеаризованной модели. На основе такой модели выполняется основной объем работ по анали- зу и синтезу системы. Уточнение результатов с учетом влияния квантования по уровню выполняется на заключительном этапе на основе имитационного моде- лирования или соответствующих аналитических оценок.

Компьютерное управление применяется для достаточно сложных объек- тов управления, в том числе нелинейных. Кроме того, закон управления, реали- зуемый компьютером, может быть нелинейным. И как отмечено выше, кванто- вание по уровню является нелинейным преобразованием. При построении ма- тематической модели системы недопустима линеаризация закона управления, а линеаризация двух других указанных нелинейностей желательна.

Основным метод линеаризации модели непрерывного объекта управле- ния основан на использовании разложения нелинейной зависимости в ряд Тей- лора с последующим сохранением только линейных членов разложения.

45

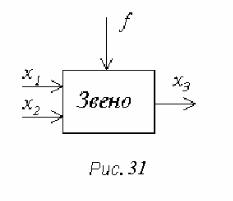
Предположим, что для нелинейного звена (рис. 31) получена модель в виде нелинейного дифференциального уравнения:

где x1 и x2 - входные сигналы, x3 - выходной сигнал, f - возмущение.

Допустим, установившийся процесс в сис-

теме имеет место при некоторых постоянных значениях x1 = x10 , x 2 = x20 , x 3 = x30 и

f = f 0 . Тогда для установившегося процесса уравнение (12.1) примет вид:

F(x10 , x20 ,0, x 30 ,0,0) = ϕ(f 0 ,0). (12.2)

В основе линеаризации лежит допущение о том, что в исследуемом динамическом процессе переменные, характеризующие состояние системы (x1 , x2 , x3 ), являются не-

прерывными функциями времени и отклоняются от установившихся значений (x10 , x 20 , x30 ) достаточно мало. Предполагается также, что F - непрерывная и

дифференцируемая по всем аргументам функция. Обозначим эти отклонения x1 , x2 , x3 . Тогда в динамическом процессе будем иметь:

x1 = x10 + Dx1, x 2 = x20 + Dx2 , x 3 = x30 + Dx3 ,

Отметим, что допущение о достаточно малых отклонениях не может быть сделано для возмущающего воздействия.

Разложим нелинейную функцию из правой части (12.1) в ряд Тейлора по всем ее аргументам. Тогда уравнение (12.1) с учетом первых членов разложе- ния примет вид:

46

æ ¶F ö 0

где ç ÷ - значение частной производной в точке, соответствующей устано-

è ¶x ø

вившемуся процессу, 0(...) - члены разложения более высокого порядка мало- сти.

После вычитания (12.2) из (12.3) получим уравнение:

которое дальше может быть записано в виде, позволяющем перейти к переда- точным функциям:

мущающее воздействие. Символы приращения при дальнейшем использова- нии уравнений вида (12.5) отбрасывают.

Из полученных соотношений видно, что рассмотренный метод линеари- зации может применяться только при условии, что функция F не имеет разры- вов первого или второго рода. Для входящих в состав компьютерной системы управления ЦАП и АЦП это условие не соблюдается. Поэтому при математиче- ском описании систем компьютерного управления рассмотренный метод ли- неаризации может применяться только для их непрерывной части. Распростра- нить его на часть системы, где выполняется квантование сигнала по уровню, невозможно.

Для линеаризации ступенчатых нелинейных характеристик ЦАП и АЦП применяется метод, основанный на допущении, противоположном использо-

47

ванному выше. Принимается, что изменения входного сигнала по своей вели- чине значительно больше единицы младшего разряда преобразователя.

Аналого-цифровое преобразование состоит в формировании двоичного кода в зависимости от величины непрерывного входного сигнала. Если на вы- ходе АЦП формируется l-разрядный двоичный код, то количество уровней его релейной статической характеристики будет равно 2l . ЦАП выполняет обрат- ное преобразование. Количество уровней его характеристики определяется раз- рядностью входного двоичного кода аналогичным образом.

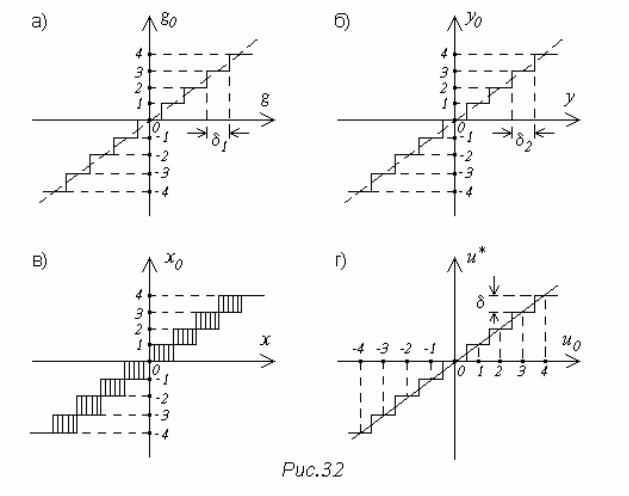
На рис. 32а показана начальная часть статической характеристики АЦП, стоящего на входе компьютерной системы управления (например, рис. 20). По горизонтальной оси отложено непрерывное значение задающего воздействия g, по вертикальной оси - его цифровое представление g0 (в десятичной системе счисления). Величина единицы младшего разряда обозначена d1 . Обычно АЦП

строят таким образом, что величина d1 постоянна для всего диапазона возмож- ных значений преобразуемого сигнала. Следовательно, характеристику АЦП можно описать зависимостью:

где E[...] - целая часть числа.

48

Линеаризация проводится путем замены ступенчатой характеристики ли- нейной, как показано на рис. 32а. Это означает, что АЦП рассматривается как безынерционное звено с передаточной функцией W(p)=k1, где коэффициент передачи определяется через величину младшего разряда преобразователя:

Наибольшая ошибка от замены нелинейной характеристики линейной не

будет превышать 0,5δ1 .

Аналогично выполняется линеаризация и для аналого-цифрового преоб- разователя управляемой величины y, статическая характеристика которого по- казана на рис. 32б. Коэффициент передачи линеаризованного звена будет ра- вен:

где δ2 - величина единицы младшего разряда преобразователя. Ошибка линеа- ризации определяется аналогичным образом.

Чаще всего задачей системы является обеспечение равенства y=g. В та-

ких случаях выбирают δ1=δ2, и рассмотренные АЦП при составлении модели могут быть условно объединены в один преобразователь - преобразователь сигнала ошибки x=g-y. Его характеристика (рис. 32в) оказывается неодно- значной. Но линеаризация для нее, выполненная рассмотренным способом, да- ет однозначный результат - безынерционное звено с коэффициентом передачи

(12.6).

На рис. 32г показана статическая характеристика ЦАП, стоящего на вы- ходе цифровой части системы. По горизонтальной оси отложена выходная ве- личина цифровой части (цифровое представление сигнала управления), по вер- тикальной оси - сигнал управления, преобразованный в непрерывную форму (чаще всего - электрическое напряжение). Единица младшего разряда преобра- зователя обозначена δ. При линеаризации ЦАП также заменяется безынерци- онным звеном, коэффициент передачи которого будет равен

Рассмотрим подробнее вопрос о погрешностях описанных моделей ЦАП и АЦП.

Для преобразователей со нелинейными статическими характеристиками, показанными на рис. 32а, б, г, может рассматриваться эквивалентная схема (рис. 33). Здесь звено 1 является линейным, с коэффициентом передачи (12.6), (12.7) или (12.8). Звено 2 обеспечивает учет погрешности линеаризованной ха- рактеристики преобразователя относительно реальной ступенчатой характери- стики. Звено 3 имеет коэффициент передачи, равный единице, и отражает ог- раничение на величину преобразуемого сигнала, связанное с конечным количе-

49