
- •СОДЕРЖАНИЕ
- •Лекция 1. Основные понятия теории автоматического управления, виды задач управления, фундаментальные принципы управления. Показатели качества управления. Базовый пример системы управления
- •Лекция 2. Передаточные функции и частотные характеристики динамических звеньев
- •Лекция 3. Структурно-динамическая схема системы. Типовые соединения динамических звеньев. Передаточные функции замкнутых систем
- •Лекция 4. Основные положения теории устойчивости. Алгебраические методы анализа устойчивости линейных систем управления
- •Лекция 5. Частотные методы анализа устойчивости систем управления
- •Лекция 6. Оценка точности систем управления. Понятия астатизма и инвариантности
- •Лекция 7. Назначение, принципы построения и основные особенности компьютерных систем управления
- •Лекция 9. Дискретные преобразования и их свойства
- •Лекция 10. Передаточные функции импульсных звеньев и систем
- •Лекция 11. Анализ устойчивости и качества импульсных систем
- •Лекция 12. Особенности построения математических моделей компьютерных систем управления. Методы линеаризации
- •Лекция 13. Передаточные функции компьютерных систем управления
- •Лекция 14. Синтез системы управления. Обеспечение точности системы
- •Лекция 15. Синтез системы управления. Обеспечение запаса устойчивости системы
- •Лекция 16. Синтез системы управления. Обеспечение запаса устойчивости системы (продолжение)
- •Лекция 17. Применение типовых ЛАХ при синтезе цифровых систем управления
- •Лекция 18. Непрерывные корректирующие звенья
- •Лекция 19. Синтез непрерывных корректирующих средств
- •Лекция 20. Синтез компьютерного управления
- •Лекция 21. Постановка задачи оптимального управления
- •Лекция 22. Синтез оптимального управления на основе вариационного исчисления
- •Лекция 23. Синтез линейного регулятора, оптимального по квадратичному критерию
- •Лекция 24. Каноническая форма уравнений Эйлера. Принцип максимума
- •Лекция 25. Синтез системы стабилизации, оптимальной по быстродействию

Для возмущающего воздействия перечень передаточных функций анало-
гичен. |
|
|
|
|
|
||
Передаточная |
функция |
разомкнутой |
системы |
по |
возмущению: |
||
Wf ( p) = |
Y ( p) |
(без |
учета главной обратной |
связи). Для рассматриваемого |
|||
|
|||||||
|
F( p) |
|
|
|
|
|
|
примера Wf ( p) = W2 ( p) . |
|
|
|
|
|||
Передаточная |
функция |
замкнутой |
системы |
по |
возмущению: |
||
Φ f ( p) = Y ( p)
F( p)
(для системы в целом). Для ее получения отметим, что уча-
сток прямой цепи системы до точки приложения возмущения при использова- нии соотношения (3.1) войдет в состав обратной связи для данного входного сигнала. В результате для рис. 11 получим:
|
|
Φ f |
( p) = |
W ( p) |
= |
|
Wf ( p) |
. |
||
|
|
2 |
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1+Wос (p)W1 |
(p)W2 ( p) |
|
1+Wос (p)W ( p) |
|
||
|
Передаточная |
функция |
по |
ошибке |
от |
возмущения: |
||||
Φxf |
( p) = |
X ( p) |
= G( p) −Y ( p) . |
Так |
как |
|
G( p) = 0 |
получаем: |
||
F( p) |
|
|||||||||
|
|
|
F( p) |
|
|
|
|
|
|
|
Φxf ( p) = −Φ f ( p). Это соотношение также носит универсальный характер.
Враспространенном на практике частном случае единичной ООС неко- торые из полученных соотношений существенно упрощаются. Если передаточ- ная функция разомкнутой системы получена в форме отношения двух полино-
мов W ( p) = QR(( pp)) , то при Wос(p)=1 нетрудно придти к следующим правилам определения передаточных функций по задающему воздействию:
Φ( p) = |
|
|
W ( p) |
= |
R( p) |
, Φx ( p) = |
1 |
= |
Q( p) |
. |
|
1 |
+W ( p) |
Q( p) + R( p) |
1+W ( p) |
Q( p) + R( p) |
|||||||
|
|
|
|
|
|||||||
Лекция 4. Основные положения теории устойчивости. Алгебраические методы анализа устойчивости линейных систем управления
Для линейных стационарных систем используется понятие асимптотиче- ской устойчивости. Систему называют устойчивой, если с течением времени переходная составляющая процесса в системе (общее решение дифференци- ального уравнения системы) стремится к нулю.
Если получено общее дифференциальное уравнение линейной стацио-
нарной системы
14
a |
|
d n x(t) |
+ a |
d n−1x(t) |
+K+a |
|
x(t) = b |
d m g(t) |
+K+b g(t), |
0 dt n |
|
|
|
||||||
|
1 dt n−1 |
|
n |
0 dtm |
m |
||||
переходная составляющая процесса в системе определяется как решение соот-
ветствующего однородного уравнения
a |
|
d n x(t) |
+ a |
d n−1x(t) |
+K+a |
n |
x(t) = 0 |
||||
|
dt n |
|
|
||||||||
и имеет вид |
0 |
|
1 |
dt n−1 |
|
|
|
||||
|
|
|
|
|
n |
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
xп(t) = åCie pit , |
|
|
|
|||
|
|
|
|
|
|
i=1 |
|
|
|
|
|
где pi - корни характеристического уравнения |
|
|
|
|
|||||||
|
|
a |
0 |
pn + a pn−1+K+a |
n |
= 0. |
|||||
|
|
|
|
|
1 |
|
|
|
|
||
Для устойчивости системы lim yп (t) = 0 необходимо и достаточно, что- t→∞
бы корни характеристического уравнения лежали в левой полуплоскости ком- плексной плоскости:
Re pi < 0. |
(4.1) |
Если имеется один или несколько вещественных корней, равных нулю, а остальные удовлетворяют условию (4.1), система находится на апериодической границе устойчивости.
Если имеется пара мнимых корней, а остальные удовлетворяют условию (4.1), система находится на колебательной границе устойчивости.
При использовании аппарата передаточных функций левая часть диффе-
ренциального уравнения системы соответствует знаменателю передаточной
функции D(p) - характеристическому полиному замкнутой системы: |
|
||||||||||||||||||||||
Ф(p) = |
|
|
W |
(p) |
|
|
b pm |
+ b pm−1+K+b |
|
p + b |
R(p) |
|
|||||||||||
|
|
|
|
|
= |
|
0 |
|
|
1 |
|
|
|
|
m−1 |
|
|
m |
= |
|
, |
||
1 |
+ W(p) |
|
n |
+ |
|
n−1+ + |
|
|
+ |
|
D(p) |
||||||||||||
|
|
|
a0 p |
a1 p |
|
|
|
an |
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
K an−1 p |
|
|
|
||||||||
|
|
|
|
|
|
|
|
W(p) = |
R(p) |
, |
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
Q(p) |
|
|
|
|
|
|
|
|
|||
D(p) = a |
0 |
pn + a pn−1 |
+K+a |
n−1 |
p + a |
n |
= R(p) + Q(p). |
|
|||||||||||||||
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Условие (4.1) неудобно для практического использования, так как задача определения корней характеристического полинома для системы высокого по- рядка может оказаться весьма трудоемкой.
Анализ устойчивости выполняется на основе системы условий и критери- ев, часть из которых обеспечивает также оценку качества системы управления и решение задач синтеза.
Необходимое условие устойчивости состоит в положительности всех ко- эффициентов характеристического полинома: ai > 0, i = 01, ,...n. Это условие
15

является необходимым и достаточным для систем первого и второго порядка.
Для устойчивости систем более высокого порядка выполнения этого условия недостаточно. В случае выполнения (4.1) анализ их устойчивости должен быть продолжен на основе одного из достаточных условий (критериев) устойчиво- сти.
Алгебраический критерий устойчивости Гурвица предусматривает анализ матрицы, составленной их коэффициентов характеристического полинома:
a1 |
a3 |
a5 ... |
0 |
a0 |
a2 |
a4 ... |
0 |
0 |
a1 |
a3 ... |
0 . |
... ... ... ... ... |
|||
0 0 0 ... an
Для устойчивости системы достаточно, чтобы были положительны n оп- ределителей Гурвица:
|
|
|
= |
|
a1 |
a3 |
|
|
= |
a1 |
a3 |
a5 |
|
|
|||
|
|
|
|
|
|
|
|
||||||||||
1 |
= a , |
2 |
|
, |
3 |
a |
0 |
a |
2 |
a |
4 |
,... |
(4.2) |
||||
1 |
|
|
a0 |
a2 |
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
0 |
a1 |
a3 |
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||
Последний n-й определитель формируется из всей матрицы. |
|
||||||||||||||||
Первый определитель положителен, если выполнено необходимое усло- вие устойчивости. Раскрывая n-й определитель по последнему столбцу, легко
убедиться, |
что n = an |
n−1. Поэтому в проверке нуждаются определители, |
начиная с |
2 и заканчивая |
n-1. |
Если |
n=0, система находится на границе устойчивости. Равенство нулю |
|
коэффициента an является признаком апериодической границы. Равенство ну- лю n-1 является признаком колебательной границы устойчивости.
Критерий Гурвица сводится к проверке неравенств, получаемых из (4.2) с учетом порядка системы. Критерий прост и удобен для компьютерной реализа- ции, однако возможности его использования для оценки качества систем и для решения задач синтеза ограничены.
Лекция 5. Частотные методы анализа устойчивости систем управления
Наиболее широкие возможности анализа и синтеза систем предоставляют частотные критерии Михайлова и Найквиста.
Критерий Михайлова предусматривает работу с характеристическим по-
линомом замкнутой системы
D(p) = a0 pn + a1 pn−1+K+an−1 p + an .
16

После подстановки p=jω получим так называемый характеристический
комплекс: |
|
( jω)n + a ( jω)n−1+K+a |
|
|
|
|
D( jω) = a |
0 |
n−1 |
jω + a |
n |
= |
|
|
1 |
|
|
|||
= X(ω) + jY(ω) = D(ω)e jψ(ω) . |
|
|
||||
Выразим характеристический комплекс через корни характеристического |
||||||
полинома: |
|
|
|
|
|
|
D( jω) = a0( jω − p1)( jω − p2)K( jω − pn ). |
|
(5.1) |
||||
Каждый сомножитель выражения (5.1) представляет собой комплексную функцию частоты, причем ψ(ω) = ψ1(ω) + ψ2(ω)+...+ψn (ω).
Если рассматривать годографы характеристического комплекса и отдель- ных сомножителей, нетрудно сделать следующие выводы:
- при изменении частоты от 0 до ∞ полный угол поворота изображающе- го вектора для D( jω) равен сумме углов поворота изображающих векторов для отдельных сомножителей;
-для отрицательного вещественного корня угол поворота изображающе- го вектора составит π 2 ;
-для положительного вещественного корня угол поворота изображающе- го вектора составит − π 2 ;
-для пары комплексно-сопряженных корней c отрицательной веществен- ной частью угол поворота изображающего вектора составит π;
-для пары комплексно-сопряженных корней c положительной вещест-
венной частью угол поворота изображающего вектора составит -π; - для нулевых корней и пар мнимых корней углы поворота изображающе-
го вектора будут равны нулю.
Следовательно, для устойчивой системы при изменении частоты от 0 до ∞ полный угол поворота изображающего вектора D( jω) на комплексной
плоскости составит n π 2 . В этом и состоит достаточное условие замкнутой
системы в соответствии с критерием Михайлова. Годограф D( jω) называется
кривой Михайлова. Отметим, что для применения критерия может не потребо- ваться трудоемкое построение кривой Михайлова на комплексной плоскости.
После раскрытия скобок в выражении D( jω) оно приводится к виду:
D( jω) = an + jan−1ω − an− 2ω2 − an−3 jω3+...
а критерий приводится к условию:
0 < ω1 < ω2 < ...< ωn ,
где 0, ω2, ω4,... - корни уравнения
Y(ω) = a |
ω − a |
ω3 |
+ a |
ω5 |
−...= 0, |
(5.2) |
|
n−1 |
n−3 |
|
n−5 |
|
|
17
ω1, ω3,... - корни уравнения |
|
X(ω) = an − an− 2ω2 + an−4ω4 −...= 0. |
(5.3) |
Колебательная граница устойчивости имеет место при одновременном выполнении X(ω) = 0 и Y(ω) = 0 на некоторой частоте ω0 , которая и явля-
ется частотой незатухающих колебаний в системе.
Критерий Михайлова дает удобный способ выбора значений параметров системы, обеспечивающих ее устойчивость, - построение области устойчивости в пространстве параметров системы.
Границы области устойчивости соответствуют границам устойчивости системы. При построении области устойчивости на основе критерия Михайло- ва, помимо апериодической и колебательной границ, рассматривается еще один предельный случай: a0=0.
Пусть требуется построить область устойчивости в m-мерном простран- стве параметров системы В=(b1,b2,...bm). Все коэффициенты характеристиче- ского полинома выражаются через параметры, а составляющие характеристи- ческого комплекса становятся функциями многих аргументов:
X = X(ω,b1,b2 ,...bm), Y = Y(ω,b1,b2 ,...bm).
Условия an (b1,b2 ,...bm) = 0 и a0(b1,b2 ,...bm) = 0 дают уравнения
границ области устойчивости как гиперплоскостей в m-мерном пространстве.
Колебательная граница устойчивости имеет место при одновременном выполнении X(ω,b1,b2 ,...bm) = 0 и Y(ω,b1,b2 ,...bm) = 0. Эти равенства
дают уравнения границы устойчивости как поверхности в m-мерном простран- стве, заданные в параметрической форме.
Наиболее распространенный на практике случай - построение области устойчивости в плоскости двух параметров.
Критерий Найквиста предусматривает анализ устойчивости замкнутой
системы по |
|
частотным характеристикам разомкнутой системы: |
||
A(ω) = |
|
W( jω) |
|
и ψ(ω) = argW( jω) или L(ω) = 20 lg A(ω) и ψ(ω). Кри- |
|
|
|||
терий Найквиста наиболее широко используется на практике по следующим причинам:
-передаточная функция и частотные характеристики для разомкнутой системы могут быть получены проще, чем для замкнутой;
-помимо анализа устойчивости обеспечивается определение ряда показа- телей качества системы;
-для анализа устойчивости и качества системы в принципе не требуется математическая модель, так как критерий допускает работу с экспериментально полученными частотными характеристиками;
-критерий Найквиста положен в основу достаточно простых и удобных процедур синтеза систем;
18

- “классический” вариант критерия разработан для случая единичной от- рицательной обратной связи, но легко распространяется и на общий случай.
Критерий Найквиста проще всего может быть получен как следствие критерия Михайлова.
Отметим следующие обстоятельства:
1. Для системы с единичной отрицательной обратной связью имеет место следующее соотношение:
1+ W( jω) = |
W( jω) |
= |
R( jω)Q( jω) |
= |
D( jω) |
|
|
|
|
. |
|||
Ф( jω) |
R( jω) |
Q( jω) |
||||
|
|
|
D( jω) |
|
|
|
Следовательно, полный угол Ψ поворота вектора 1+ W( jω) вокруг на- чала координат (или вектора W( jω) вокруг точки (-1,0) на комплексной плос- кости) равен разности углов Ψ1 поворота вектора D( jω) и Ψ2 поворота векто- ра Q( jω).
2.Для устойчивой системы при изменении частоты от -∞ до ∞ полный угол поворота вектора D( jω) на комплексной плоскости составит nπ.
3.Полный угол поворота вектора Q( jω), соответствующего знаменате-
лю передаточной функции разомкнутой системы, изменении частоты от -∞ до ∞ составит nπ-2lπ, где l - количество корней знаменателя передаточной функ- ции разомкнутой системы, лежащих в правой полуплоскости.
Следовательно, для устойчивости замкнутой системы достаточно, чтобы при изменении частоты от -∞ до ∞ вектор W( jω) поворачивался относи-
тельно точки (-1,0) на комплексной плоскости на угол величиной 2lπ в положи- тельном направлении, то есть против часовой стрелки, где l - количество кор- ней знаменателя передаточной функции разомкнутой системы, лежащих в пра- вой полуплоскости. В этом и состоит основная формулировка критерия устой- чивости Найквиста.
Очевидно, в случае устойчивости разомкнутой системы l=0, и такой угол поворота должен быть равен нулю - годограф W( jω) не должен охватывать
точку (-1,0).
Если разомкнутая система находится на границе устойчивости, использу- ется формальный прием, позволяющий отнести соответствующие корни знаме- нателя к левой полуплоскости. Поскольку на частотах, соответствующих нуле- вым и мнимым корням Q( jω), годограф W( jω) уходит в бесконечность и
претерпевает разрывы, он дополняется на этих частотах дугами бесконечного радиуса. Это эквивалентно добавлению к величине нулевых и мнимых корней бесконечно малой отрицательной вещественной части. С учетом таких допол- нений критерий применяется в сформулированном выше виде.
19
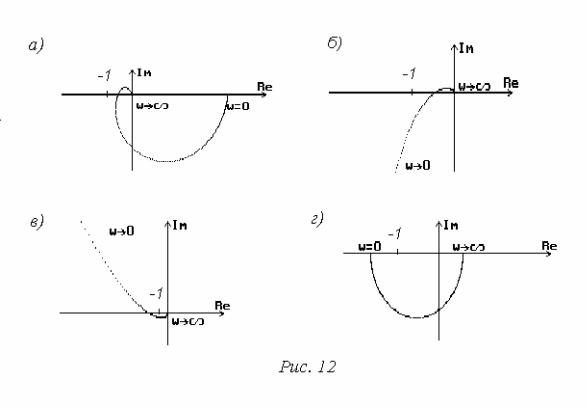
На рис. 12-14 представлены примеры систем со следующими передаточ- ными функциями:
а) W(p) = |
|
|
K |
|
, б) W(p) = |
|
|
K |
|
|
|
|
, |
||||||
(T p +1)(T p +1)(T p +1) |
p(T p +1)(T p +1) |
||||||||
|
1 |
2 |
3 |
1 |
2 |
|
|||
в) W(p) = |
K(T p +1)2 |
, г) W(p) = |
|
K |
|
|
|||
|
1 |
|
|
|
. |
|
|
||
p3(T p +1) |
(T1 p +1)(T2 p −1) |
|
|
||||||
|
|
2 |
|
|
|
|
|
|
|
20
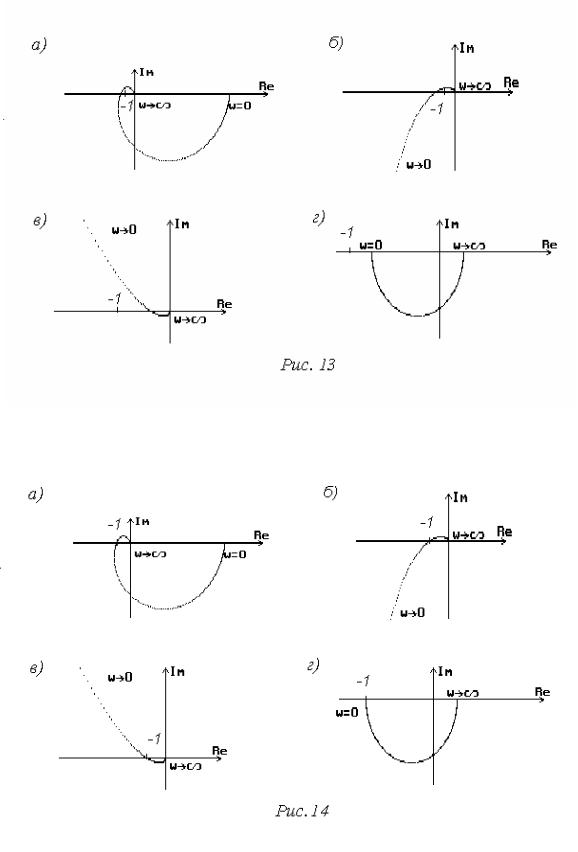
На рис. 12 системы устойчивы, на рис. 13 - неустойчивы, на рис. 14 - на- ходятся на границе устойчивости.
Отметим важный для практики случай - условно устойчивая система (рис. 12в). Условно устойчивой называется устойчивая система, которая может потерять устойчивость за счет уменьшения коэффициента передачи. Практиче- ское построение таких систем нежелательно, так как потеря
21
