
- •1. ИНФОРМАЦИЯ, ЕЁ СВОЙСТВА, ИЗМЕРЕНИЕ, ПРЕДСТАВЛЕНИЕ И КОДИРОВАНИЕ
- •1.1. Информатика – предмет и задачи
- •1.2. Информация, ее виды и свойства
- •1.3. Представление об информационном обществе
- •1.4. Кодирование информации
- •1.5. Практическое занятие № 1. Системы счисления. Перевод чисел из одной системы счисления в другую. Арифметические операции в позиционных системах счисления
- •1.6. Кодирование текстовых и символьных данных
- •1.7. Кодирование графических данных
- •1.8. Кодирование звуковой информации
- •1.9. Структуры данных
- •1.10. Файлы и файловая структура
- •1.11. Измерение и представление информации
- •1.12. Теоремы Шеннона
- •1.13. Математические основы информатики
- •1.13.1. Алгебра высказываний (алгебра логики)
- •1.13.2. Элементы теории множеств
- •2. ВЫЧИСЛИТЕЛЬНАЯ ТЕХНИКА
- •2.1. История развития вычислительной техники
- •2.2. Классификация компьютеров по сферам применения
- •2.3. Базовая система элементов компьютерных систем
- •2.4. Функциональные узлы компьютерных систем
- •2.5. Архитектура ЭВМ
- •2.6. Совершенствование и развитие архитектуры ЭВМ
- •2.6.1. Архитектуры с фиксированным набором устройств
- •2.6.2. Открытая архитектура
- •2.6.3. Архитектура многопроцессорных вычислительных систем
- •2.7. Внутренняя структура ЭВМ
- •2.7.4. Внешние запоминающие устройства
- •2.8. Внешние устройства компьютера
- •2.8.1. Видеотерминалы
- •2.8.2. Устройства ручного ввода информации
- •2.8.3. Устройства печати
- •2.8.4. Устройства поддержки безбумажных технологий
- •2.8.5. Устройства обработки звуковой информации
- •2.8.6. Устройства для соединения компьютеров в сеть
- •3. ПРОГРАММНОЕ ОБЕСПЕЧЕНИЕ ЭВМ
- •3.1. Состав системного программного обеспечения
- •3.2. Операционные системы
- •3.3. Виды операционных систем и их базовые понятия
- •3.4. Процессы и потоки
- •3.5. Управление памятью
- •3.6 Организация ввода-вывода
- •3.7 Драйверы устройств
- •3.8 Файловые системы
- •3.9 Файловые системы Microsoft Windows
- •3.9.1. Файловая система FAT16
- •3.9.3. Файловая система NTFS
- •3.9.4. Сравнение файловых систем FAT16, FAT32 и NTFS
- •3.10 Операционная система Windows
- •3.11 Служебные программы
- •3.13 Прикладное программное обеспечение
- •3.13.1. ППО общего назначения
- •3.13.2. ППО специального назначения
- •3.17. Практическое занятие № 6. Табличный процессор Excel. Основные понятия и общие принципы работы с электронной таблицей. Создание и заполнение таблиц постоянными данными и формулами. Построение диаграмм и графиков
- •3.18. Практическое занятие № 7. Табличный процессор Excel. Сортировка и фильтрация (выборка) данных. Сводные таблицы, структурирование таблиц. Расчёты в Excel
- •4. БАЗЫ ДАННЫХ (БД) И СИСТЕМЫ УПРАВЛЕНИЯ БАЗАМИ ДАННЫХ (СУБД)
- •4.1. Базы данных в структуре информационных систем
- •4.2. Классификация баз данных и виды моделей данных
- •4.3. Нормализация отношений в реляционных базах данных
- •4.4. Проектирование баз данных
- •4.5. Этапы развития СУБД. Реляционная СУБД Microsoft Access – пример системы управления базами данных
- •4.6. Практическое занятие № 8. СУБД Access 97. Создание однотабличной базы данных. Отбор данных с помощью фильтра. Формирование запросов и отчётов для однотабличной базы данных
- •5. КОМПЬЮТЕРНЫЕ СЕТИ И ОСНОВЫ ЗАЩИТЫ ИНФОРМАЦИИ
- •5.1. Назначение и классификация компьютерных сетей
- •5.2. Режимы передачи данных в компьютерных сетях
- •5.3. Типы синхронизации данных при передаче и способы передачи информации
- •5.4. Аппаратные средства, применяемые при передаче данных
- •5.5. Архитектура и протоколы компьютерных сетей
- •5.6. Локальные вычислительные сети (ЛВС) и их топологии
- •5.7. Физическая передающая среда ЛВС и методы доступа к ней
- •5.8. Примеры сетей. Глобальная сеть Интернет
- •5.9. Службы сети Интернет
- •5.10. Поиск информации в Интернет
- •5.10.1. Поисковые машины
- •5.12. Основы и методы защиты информации
- •5.13. Политика безопасности в компьютерных сетях
- •5.14. Способы и средства нарушения конфиденциальности информации
- •5.15. Основы противодействия нарушению конфиденциальности информации
- •5.16. Криптографические методы защиты данных
- •5.17. Компьютерные вирусы и меры защиты информации от них
- •6. ОСНОВЫ АЛГОРИТМИЗАЦИИ И ТЕХНОЛОГИИ ПРОГРАММИРОВАНИЯ. МОДЕЛИ И ИНФОРМАЦИОННОЕ МОДЕЛИРОВАНИЕ
- •6.1. Алгоритм и его свойства
- •6.1.2. Графическое представление алгоритмов
- •6.2. Принципы разработки алгоритмов и программ для решения прикладных задач
- •6.2.1. Процедурное программирование
- •6.2.3. Функциональное программирование
- •6.2.4. Логическое программирование
- •6.2.5. Объектно-ориентированное программирование (ООП)
- •6.3. Методы и искусство программирования
- •6.4. Обзор языков программирования
- •6.5. Понятие о метаязыках описания языков программирования
- •6.6. Моделирование как метод решения прикладных задач
- •6.7. Основные понятия математического моделирования
- •6.8. Информационное моделирование
- •6.9. Практическое занятие № 11. Вычисления в среде Mathcad
- •6.10. Практическое занятие № 12. Вычисления в среде Matlab
- •СПИСОК ЛИТЕРАТУРЫ
- •ОГЛАВЛЕНИЕ

Из этой таблицы видно, что число различных двоичных наборов длины n x1, x2 ,..., xn
конечно и равно 2n .
Ясно, что тавтологии и тождественно ложные функции алгебры логики представляют собой постоянные функции, а две равносильные формулы выражают одну и ту же функцию. Каждая функция определяется таблицей истинности, состоящей из 2n строк, то есть
принимает 2n значений (каждое 0 или 1). Общее число наборов из 0 и 1 длины 2n равно 22n Это число равно числу различных функций алгебры логики n переменных.
Каждой формуле алгебры логики соответствует своя функция. Если формулы A и B эквивалентны, то соответствующие им функции равны: f A (x1 , x2 ,..., xn ) = fB (x1, x2 ,..., xn ). Это
значит, что при всех значениях переменных x1, x2 ,..., xn значения f A и fB совпадают.
Каждая булева функция может быть путем эквивалентных преобразований приведена к двум особым формам, которые называются дизъюнктивной и конъюнктивной
нормальными формами. Пусть |
x1, x2 ,..., xn переменные булевой функции |
f (x1, x2 ,...,xn ), а |
||||||||||||||||||||
σ1,σ 2 ,...,σ 3 - набор этих переменных. Введем обозначение: xσ = xσ Ú |
|
|
|
, |
где σ - параметр, |
|||||||||||||||||
x |
σ |
|||||||||||||||||||||
|
|
|
|
ì |
|
, |
σ = 0, |
|
|
|
|
|
|
|
|
|||||||
равный 0 или 1. Очевидно, |
|
что |
xσ = |
x |
Тогда |
функцию |
|
f (x , x |
2 |
,...,x |
n |
) можно |
||||||||||
|
|
|
|
|
|
í |
|
|
σ = 1. |
|
|
|
1 |
|
|
|
||||||
|
|
|
|
|
|
îx, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
представить в виде: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
f (x , x |
2 |
,...,x |
n−1 |
, x |
n |
)= |
|
Ú |
|
xσ1 |
Ù xσ2 Ù...xσn , |
|
(1.13.4) |
|||||||||
1 |
|
|
|
|
|
σ1,σ2 ,...,σn , |
1 |
2 |
n |
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
f (σ1,σ 2 ,..., σ n )=1 |
|
|
|
|
|
|
|
|
|
|
|
|
||
где дизъюнкция берется по всевозможным наборам значений переменных x1 , x2 ,..., xm или
f (x , x |
2 |
,...,x |
n |
)= |
Õ |
|
|
xσ1 |
Ú xσ2 |
Ú...Ú xσn , |
(1.13.5) |
||||
1 |
|
|
f ( |
|
, |
|
,..., |
|
)=0 |
1 |
2 |
n |
|
||
|
|
|
|
|
σ1 |
σ2 |
σn |
|
|
|
|
||||
где символ Õ означает, что конъюнкции берутся по тем наборам переменных, которые
указаны под ним. Нормальные формы позволяют дать критерий равносильности двух произвольных формул A и B .
Аппарат булевых функций используется для проектирования цифровых устройств и базовых элементов компьютерных систем.
1.13.2. Элементы теории множеств. Первичным понятием теории множеств является понятие самого множества. Множество – это совокупность некоторых (произвольных) объектов, объединенных по какому-либо признаку. Элементы множества при этом должны быть различными. Множество обозначается парой скобок {...}, внутри которых либо просто
перечисляются элементы, |
либо описываются их свойства. Например, A = {x Î N x + 2 = 1} - |
||||||
множество натуральных |
чисел, |
удовлетворяющих |
условию |
x + 2 = 1, очевидно, |
пусто. |
||
B = { сложение, умножение } - |
множество основных арифметических операций. |
Пустое |
|||||
множество обозначается |
знаком Æ. Если необходимо указать, что объект a |
является |
|||||
элементом множества A , |
то пишут a Î A ( a принадлежит A ), наоборот запись |
a Ï A |
|||||
говорит о том, что a не принадлежит A . |
|
|
|
|
|||
Если каждый элемент множества A является элементом множества B , то пишут |
|||||||
A Í B или B Ê A и говорят, что множество A является подмножеством множества B . |
|||||||
Если A есть подмножество множества B , причем |
A ¹ B , то пишут A Ì B или |
B É A . |
|||||
Множества, состоящие из одних и тех же элементов, |
называются равными, то есть A = B , в |
||||||
противном случае A ¹ B . С помощью скобок и операций над множествами можно построить |
|||||||
новые множества, более сложные чем исходные. |
|
|
|
|
|||
Объединение |
(или |
сумма). Эта операция над множествами обозначается |
|
A È B , |
|||
определяется как |
C = A È B = {x ÎC (x Î A)Ú (x Î B)}. Все |
операции над множествами |
|||||
35

можно иллюстрировать с помощью диаграмм Эйлера - Венна . Если за некоторое универсальное множество, содержащее как подмножества все другие множества, обозначить U (или Ω ) и изобразить его в виде всей плоскости, то любое множество A U можно изобразить в виде части плоскости, то есть в виде некоторой фигуры, лежащей на плоскости. Множество C объединение множеств A и B , C на рис. 1.7 заштриховано. C = A B .
U U
A B A B
Рис. 1.8
Пересечением (или произведением) двух множеств называется такое множество C , которое состоит из элементов, принадлежащим одновременно обоим множествам, то есть C = A Ç B = {x ÎC (x Î A)Ù (x Î B)}. Пересечение множеств A и B заштриховано и изображено на рис. 1.8.
(x Î A)Ù (x Î B)}. Пересечение множеств A и B заштриховано и изображено на рис. 1.8.
Разностью двух множеств A и B называется множество A \ B , состоящее из тех и только тех элементов, которые входят в A и одновременно не входят в B , то есть
C = A \ B = {x ÎC (x Î A)Ù (x Ï B)}= AÇ B (см. рис 1.9). Если, в частности, |
A подмножество |
|||||||
U , то разность U \ A обозначается A и называется дополнением множества A (см. рис |
||||||||
1.10). |
|
|
|
|
|
|
|
|
|
|
U |
|
|
|
|
U |
|
|
A |
B |
|
|
|
|
|
|
|
|
|
|
|
A |
|
|
|
|
|
|
|
|
|
|
A |
|
|
|
Рис. 1.9 |
|
Рис. 1.10 |
|
|
|
|
|
|
|
|
|
|
|
||
Симметрической разностью или кольцевой суммой множеств A и B называется |
||||||||
множество |
C = AÅ B = (A \ B)È (B \ A) |
(см. |
рис |
1.11). |
Очевидно, |
что |
||
C = AÅ B = {x ÎC /((x Î A)Ù (x Ï B))Ú ((x Ï A)Ù (x Î B))}. |
Если |
a A |
и |
b B , то |
пару |
|||
элементов (a, b) называют упорядоченной парой, причем пары (a1, b1 ) и (a2 , b2 ) равны тогда
и только тогда, когда a1 = a2 |
и b1 = b2 . |
Множество, элементами которого являются все |
|||||||
|
|
U |
|
||||||
|
|
упорядоченные пары (a,b), a A , b B |
называется |
||||||
|
|
|
|||||||
|
|
|
прямым или декартовым произведением множеств |
A |
|||||
A |
B |
|
и |
B |
и |
обозначается |
A × B. |
Например, |
|
|
|
A B A = {1,2}, |
B = {2,3}® A ´ B = {(1,2), (1,3), (2,2), (2,3)}, |
а |
|||||
|
|
|
B ´ A = {(2,1), (2,2), (3,1), (3,2)}. |
Таким |
образом, |
||||
|
|
|
декартово |
произведение |
не |
подчиняется |
|||
|
Рис. 1.11 |
|
коммутативному закону и A × B = B × A справедливо, |
||||||
|
|
|
|
|
|
|
|
|
|
Леонард Эйлер (1707 - 1783) - швейцарский математик.
Джон Венн (1834 - 1923) - английский математик и логик.
36

если A = B. Произведение A × A называется декартовым квадратом.
Свойства операций объединения, пересечения и дополнения иногда называются законами алгебры множеств. Эти законы аналогичны правилам для равносильностей в булевой алгебре (1.13.1) –(1.13.3).
Часто элементы разных множеств связаны различными соотношениями, например,
соотношениями порядка. n -местным отношением или n -местным предикатом P на множествах A1, A2 ,..., An называется любое подмножество декартова произведения
A1 ´ A2 ´...´ An . Обозначение n -местного отношения P(x1 , x2 ,...,xn ). При n = 1 отношение P называется унарным и является подмножеством множества A1 . Бинарным (или двуместным при n = 2 ) отношением называется множество упорядоченных пар. Элементы x1,x2 ,..., xn
называются координатами или компонентами отношения P .
В теории множеств важную роль играют два вида специальных бинарных отношений:
отношения эквивалентности и отношения порядка. Прообразами этих отношений служат
интуитивные понятия равенства, предшествования и предпочтения. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||
Рассмотрим два конечных множества A = {a1 ,a2 ,...,an }, |
B = {b1,b2 ,...,bm } и бинарное |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
отношение |
P A× B . Введем матрицу |
|
|
|
P |
|
|
|
= (pi, j ) бинарного отношения |
|
P |
следующим |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
ì1, (ai ,bj |
)Î P, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
образом: pi, j = îí0, (ai ,bj |
)Ï P. Эта матрица содержит полную информацию о связях между |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
элементами множеств A и B и позволяет представить эту информацию в графическом виде. |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Матрица любого бинарного отношения обладает следующими свойствами: |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
q |
если P,Q Í A´ B |
и |
|
|
|
P |
|
|
|
= (pi, j ), |
|
|
|
Q |
|
|
|
= (qi, j |
), то |
|
|
|
P ÈQ |
|
|
|
= |
|
|
|
P |
|
|
|
+ |
|
|
|
Q |
|
|
|
= (pi, j + qi, j ); |
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
P ÇQ |
|
|
|
= |
|
|
|
P |
|
|
|
* |
|
|
|
Q |
|
|
|
= (pi, j ×qi, j ), |
|
|
|
|
причем |
сложение |
|
|
|
|
элементов |
матрицы |
|||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
осуществляется по правилам 0+0=0, 1+1=1, 1+0=0+1=1, а умножение |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
осуществляется |
почленно |
|
|
обычным |
образом, |
т. е. |
|
по |
правилам |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
1×0 = 0×1 = 0, 1×1 = 1; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
q
 P−1
P−1 
 =
= 
 P
P
 T , где
T , где 
 P−1
P−1 
 - матрица обратного отношения P−1 ;
- матрица обратного отношения P−1 ;
q если P Í Q , то |
|
|
|
P |
|
|
|
|
= (pi, j ), |
|
|
|
|
Q |
|
|
|
= (qi, j ) и pi, j |
£ qi, j . |
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Пример 1. |
Бинарное отношение |
P Í A2 , A = {1,2,3} |
изображено на рис. 1.12. Его |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
æ |
0 |
1 |
1ö |
|
|
|
|
|
|
|
|
|
|
|
æ |
1 |
0 |
1 |
ö |
|
||
|
|
|
|
|
|
|
матрица имеет вид |
|
P |
ç |
0 |
1 |
÷ |
. Пусть |
|
|
|
Q |
|
|
ç |
0 |
0 |
1 |
÷ |
, тогда |
||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
= ç |
1÷ |
|
|
|
|
|
= ç |
÷ |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ç |
|
|
|
|
÷ |
|
|
|
|
|
|
|
|
|
|
|
ç |
0 1 0 |
÷ |
|
||
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
è |
1 0 1ø |
|
|
|
|
|
|
|
|
|
|
|
è |
ø |
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
æ |
1 |
1 |
1ö |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
æ |
0 |
0 |
1 |
ö |
|
||||||
|
|
|
|
|
|
|
|
|
|
|
P È Q |
|
|
|
|
|
|
|
|
|
P |
|
Q |
|
ç |
|
|
|
÷ |
, |
|
P ÇQ |
|
P |
|
|
|
Q |
|
|
|
ç |
0 0 1 |
÷ |
|
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
= |
|
|
|
|
+ |
|
= ç |
0 1 1÷ |
|
= |
|
* |
|
|
|
|
= ç |
÷ . |
|||||||||||||||||||||||||||||||||||||||||||||
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ç |
1 |
|
÷ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ç |
0 |
0 |
0 |
÷ |
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
è |
1 1ø |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
è |
ø |
|
|||||||||||
Рис. 1.12 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Пусть P - бинарное отношение на множестве |
A , |
P Í A2 . |
|||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
Отношение |
|
P |
|
|
|
|
на множестве A называется рефлексивным, если |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
æ 1 |
* |
|
|
|
|
|
* |
* ö |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||
|
ç |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
÷ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
"x Î A, (x, x)Î P , |
т. е. |
|
|
|
P |
|
|
|
ç * |
1 |
|
|
|
|
|
* |
* |
÷ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
= ç |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
÷ , где звездочкой обозначены нули или единицы. |
|||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
ç... ... ... |
... |
÷ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||
|
ç |
|
|
|
|
* |
|
|
|
|
|
* |
1 |
÷ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||
|
è * |
|
|
|
|
|
ø |
|
|
|
|
|
|
"x Î A, (x, x)Ï P . |
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||
Отношение P называется иррефлексивным, если |
Отношение |
P на |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
множестве A называется симметричным, |
|
если "x, y Î P из условия (x, y)Î P следует, что |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
(y, x)Î P . Это значит, что |
|
|
|
P |
|
|
|
T |
= |
|
|
|
P |
|
|
|
. Отношение P называется антисимметричным, если из |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
37
условий (x, y)Î P |
и (y, x)Î P следует, что x = |
y , или |
|
P Ç P−1 |
|
= |
|
|
|
P |
|
|
|
* |
|
|
|
P |
|
|
|
T . |
Это свойство |
||||||||||||
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
приводит к тому, |
что |
у матрицы |
|
P Ç P−1 |
|
|
|
|
все элементы вне главной диагонали будут |
||||||||||||||||||||||||||
|
|
|
|||||||||||||||||||||||||||||||||
нулевыми (на главной диагонали тоже могут быть нули). Отношение |
P |
называется |
|||||||||||||||||||||||||||||||||
транзитивным, если из (x, y)Î P и (y, z)Î P следует, что (x, z)Î P . |
|
|
|
||||||||||||||||||||||||||||||||
Рефлексивное, транзитивное и симметричное отношение на множестве A называется |
|||||||||||||||||||||||||||||||||||
эквивалентностью на |
A . |
Эквивалентность обозначается символами E или ~, например, |
|||||||||||||||||||||||||||||||||
xEy , x ~ y . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Пример 2. Докажем, что на множестве N ´ N отношение Q является отношением |
|||||||||||||||||||||||||||||||||||
эквивалентности, если {(a,b),(c,d )}ÎQ Û a + d = b + c . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
Если отношение Q рефлексивно на A , |
то "x ÎQ (x, x)ÎQ . В нашем случае роль A |
||||||||||||||||||||||||||||||||||
играет множество |
N ´ N , |
а роль |
элемента |
x играет пара (x, y). Тогда |
отношение |
Q |
|||||||||||||||||||||||||||||
рефлексивно на N ´ N , если "(x, y)ÎQ {(x, y),(x, y)}ÎQ . |
По определению Q : a + d = b + c , |
||||||||||||||||||||||||||||||||||
но a + b = b + a , следовательно, Q рефлексивно. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
Аналогично, если |
{(a,b),(c,d )}ÎQ , то |
и |
{(c,d ),(a,b)}ÎQ , так как из |
a + d = b + c |
|||||||||||||||||||||||||||||||
следует, что c + b = d + a . Таким образом, |
Q симметрично. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
Наконец, если |
{(a,b),(c,d )}ÎQ , |
{(c,d ),( f , g)}ÎQ , то |
{(a,b),( f , g)}ÎQ , так |
как |
|||||||||||||||||||||||||||||||
a + d = b + c и |
c + g = d + f . |
Тогда |
(a + d )+ (c + g) = (b + c)+ (d + f )Þ a + d + c + g = |
||||||||||||||||||||||||||||||||
= b + c + d + f Þ a + g = b + f , т. е. Q транзитивно. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
Рефлексивное, транзитивное и антисимметричное отношение на |
множестве |
A |
|||||||||||||||||||||||||||||||||
называется частичным порядком на A . Частичный порядок обозначается символом ≤ , а |
|||||||||||||||||||||||||||||||||||
обратное ему отношение £−1 символом ³ . Отношение < |
называется строгим порядком и |
||||||||||||||||||||||||||||||||||
определяется таким образом x < y Û x £ y и x ¹ y . Это отношение не является частичным порядком, так как не удовлетворяет условию рефлексивности x < x .
Если во множестве A |
есть элементы x и y , о которых нельзя сказать, что x ≤ y или |
y £ x , то такие элементы |
называются несравнимыми. Частичный порядок называется |
линейным порядком, если любые два элемента x и y из множества A сравнимы, т. е. |
x ≤ y |
||||||
или y £ x . |
|
|
|
|
|
|
|
Непустое множество A , на котором зафиксирован некоторый частичный (линейный) |
|||||||
порядок, называется частично (линейно) упорядоченным |
множеством. Элемент |
a Î A |
|||||
частично упорядоченного множества A называется максимальным (минимальным), если для |
|||||||
"x Î A из того, что |
a £ x (x £ a) |
следует |
a = x . Элемент |
a Î A называется наибольшим |
|||
(наименьшим), если |
x £ a (a £ x) |
для всех "x Î A . Наибольший |
элемент обозначается |
||||
max A , наименьший - |
min A . Этих элементов у множества может и не быть, например, |
||||||
линейно упорядоченное множество рациональных чисел |
(0,1] не имеет наименьшего |
||||||
элемента, наибольший элемент равен единице. |
|
|
|
|
|||
Верхней (нижней) гранью подмножества B частично упорядоченного множества |
A |
||||||
называется всякий элемент a Î A и такой, |
что b £ a (a £ b) |
для всех bÎ B . Точной верхней |
|||||
(нижней) гранью подмножества |
B Í A |
называется наименьшая |
верхняя (наибольшая |
||||
нижняя) грань для |
B . Точная верхняя и точная нижняя грани множества |
B Í A |
|||||
обозначаются через sup B (супремум) и inf B (инфимум) соответственно. |
|
|
|||||
Линейный порядок £ на множестве A называется полным, |
если каждое непустое |
||||||
подмножество множества A имеет наименьший элемент. |
В этом |
случае множество |
A |
||||
называется вполне упорядоченным. |
|
|
|
|
|
|
|
1.13.3. Элементы теории графов. Граф задается |
парой |
множеств. Пусть |
S - |
||||
непустое множество, |
V (2) - множество всех его двухэлементных подмножеств, U Ì V (2). |
||||||
38

Тогда пара (S,U ) называется неориентированным графом. Элементы множества S называются вершинами графа, а элементы множества U - ребрами. Итак, G = (S,U ) граф -
это конечное множество вершин S и множество ребер U .
Вершины графа обозначают по-разному: или большими буквами, или малыми с индексами; для ребер наиболее употребительное обозначение - u с индексом, например, u1, u2 ,...,un . Взаимное расположение, форма и длина ребер значения не имеют. Важно лишь
то, что они соединяют две данные вершины множества S .
Если в |
паре |
вершин xi и x j |
указано направление связи, т. е. какая из вершин |
|
является первой, то соединяющий |
их отрезок uk называется |
дугой, а вершины, |
||
определяющие |
дугу |
uk , называют |
концевыми вершинами. Если |
концевые вершины |
совпадают, то дугу называют петлей. В графе G могут существовать дуги (ребра) с одинаковыми концевыми вершинами. Такие дуги называются параллельными.
Если в графе G = (S,U ) все элементы множества U изображаются дугами, то граф
называется ориентированным или орграфом, если ребрами, то неориентированным. Два ребра называются смежными, если они имеют общий конец.
Вершина x1 и ребро u1 называются инцидентными, если x1 является концом ребра u1
и не инцидентными в противном случае. Таким образом, смежность есть отношение между однородными элементами графа, тогда как инцидентность является отношением между разнородными элементами.
Число вершин графа называется его порядком. Степенью P(xi ) вершины xi
называется число дуг (ребер) графа G , инцидентных данной вершине. Вершина степени нуль называется изолированной, а если степень равна единице, то такая вершина называется
висячей.
Граф G называется простым, если он не содержит петель и параллельных дуг. Простой граф, в котором каждая пара вершин смежна, называется полным. Граф, содержащий хотя бы две параллельные дуги (ребра), называется мультиграфом. Граф, содержащий петли, называется псевдографом.
Графы удобно изображать в виде рисунков, состоящих из точек и линий, соединяющих некоторые из этих точек. Два графа G и G1 называются изоморфными, если
между множеством их вершин существует такое взаимно однозначное соответствие, при котором в одном из графов ребрами соединены вершины в том и только в том случае, если в другом графе ребрами соединены те же вершины. Для орграфов ориентация дуг должна быть также одинаковой.
Очевидно, что отношение изоморфизма графов является эквивалентностью, т. е. оно симметрично, транзитивно и рефлексивно. Следовательно, множество всех графов разбивается на классы так, что графы из одного класса попарно изоморфны, а графы из разных классов не изоморфны.
Способов задания графов – великое множество. Самый простой способ – задание множеств S и U . Граф также может быть задан просто рисунком. В силу изоморфизма один и тот же граф может быть изображен разными рисунками.
Граф называется плоским (планарным), если он может быть изображен на плоскости так, что все пересечения ребер являются его вершинами.
|
|
Для произвольного |
графа |
G = (S,U ) |
следующим |
||||
|
|
образом |
определяется |
дополнительный |
граф |
||||
|
|
(дополнение) |
~ |
~ |
этом |
графе |
~ |
вершин |
|
|
|
G = (S,U ). В |
G |
||||||
|
|
столько |
же, |
сколько |
в графе G , |
причем |
любые две |
||
G=(S,U) |
G=(S,U) |
|
|
|
|
|
~ |
|
|
|
|
несовпадающие вершины смежны в G тогда и только |
|||||||
Рис. 1.13 |
тогда, когда они не смежны в G |
(см. рис. 1.13). |
|
39

Чередующая последовательность |
x1, u1, x2 , u2 ,..., xk , uk , xk+1 вершин и ребер |
графа, |
|||
такая что |
ui = xi xi+1, i = |
1, k |
, называется |
маршрутом, соединяющим вершины x1 |
и xk+1 . |
Очевидно, |
что маршрут можно задать последовательностью его вершин x1, x2 ,..., xk+1 или |
||||
последовательностью ребер u1,u2 ,...,uk . |
Маршрут называется цепью, если все его |
ребра |
|||
различны, и простой цепью, если все его вершины, кроме, возможно, крайних, различны. Гамильтоновой цепью называется простая цепь, содержащая все вершины графа.
Маршрут называется циклическим, если x1 = xk+1 . Циклическая цепь называется
циклом, а циклическая простая цепь – простым циклом. Число ребер в маршруте называется длиной маршрута. Гамильтоновым циклом называется простой цикл, содержащий все вершины графа. Длина всякого цикла не менее трех в графе без петель и кратных ребер. Минимальная из длин циклов графа называется его обхватом.
Важным понятием теории графов является связность. Граф называется связным, если любые две его несовпадающие вершины соединены маршрутом.
В подавляющем большинстве случаев граф задается матрицей. Для расчетов на ЭВМ это единственный способ. Наиболее часто граф задают с помощью матриц смежности и
|
B |
u3 |
|
инциденций. Рассмотрим изображенный на рисунке 1.14 граф. Как |
||||||
|
|
D |
|
для орграфов, так и для неориентированных |
графов можно |
|||||
u2 |
|
u4 |
|
определить матрицу смежности вершин. Это квадратная матрица |
||||||
A |
|
|
|
|
|
A |
B |
C |
D |
E |
|
|
u9 |
|
u8 |
A |
|||||
u6 |
|
|
|
æ0 1 1 0 0ö |
||||||
u5 |
|
|
E |
|
B |
ç |
|
|
|
÷ |
|
|
|
ç1 |
0 |
0 |
1 |
0÷ |
|||
|
|
u7 |
|
P = |
||||||
C |
|
|
C |
ç |
0 |
0 |
0 |
÷ |
||
Рис. 1.14 |
|
|
ç1 |
1÷ |
||||||
|
|
D |
ç0 |
1 |
0 |
0 |
0÷ |
|||
|
|
|
|
|
||||||
|
|
|
|
|
E |
ç |
0 |
0 |
1 |
÷ |
|
|
|
|
|
è0 |
1ø |
||||
n × n порядка, где n - число вершин. Ее строки и столбцы соответствуют вершинам графа. Элементы pij матрицы смежности вершин равны числу дуг, идущих из i - той вершины в
j -ю вершину. Если орграф не содержит параллельных дуг, то матрица является бинарной и состоит только из нулей и единиц. В случае неориентированного графа ему вместе с ребром xi x j принадлежит и ребро x j xi , поэтому матрица смежности вершин будет симметрической.
Матрица смежности вершин однозначно определяет структуру графа. Аналогично можно
определить и матрицу смежности дуг. |
|
|
|
|
|
|
Определим для рассматриваемого графа без ребра u9 матрицу инциденций. Это |
||||||
прямоугольная матрица размерности |
n × m , |
где |
n - число вершин, а m - число дуг. |
|||
Элементы |
rij этой матрицы равны плюс единице, |
если дуга |
uj |
исходит из i -й вершины |
||
(начальная |
вершина), минус единице, |
если |
дуга |
uj входит |
в |
i -ю вершину (конечная |
вершина), нулю, |
если дуга не инцидентна i -й вершине. В случае неориентированного графа |
||||||||
элементами |
матрицы |
будут |
числа |
единица |
и |
нуль, |
т. |
е. |
|
ì 1, вершина xi инцидентна ребру u j |
, |
Строки матрицы |
|
инциденций |
называют |
||||
rij = í |
|
|
|
|
|||||
î0, вершина xi не инцидентна ребру u j . |
|
|
|
|
|
|
|||
векторами инциденций графа G. Матрица инциденций
40
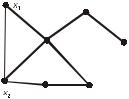
|
A |
|
u1 |
u2 |
u3 |
u4 |
u5 |
u6 |
u7 |
u8 |
|
|
æ 1 -1 |
0 |
0 |
-1 1 |
0 |
0 ö |
|||||
|
B |
ç |
-1 |
1 |
1 -1 |
0 |
0 |
0 |
0 |
÷ |
|
R = |
ç |
÷ |
|||||||||
C |
ç |
0 |
0 |
0 |
0 |
1 |
-1 |
1 |
0 |
÷ |
|
|
D |
ç |
|
0 |
-1 1 |
0 |
0 |
0 |
|
÷ |
|
|
ç 0 |
-1÷ |
|||||||||
|
E |
ç |
0 |
0 |
0 |
0 |
0 |
0 |
-1 1 |
÷ |
|
|
è |
ø |
|||||||||
также однозначно определяет структуру графа.
Весьма важным видом графа является связный граф, не имеющий циклов, он называется деревом. В дереве любые две вершины связаны единственным путем.
Рассмотрим связный граф G = (S,U ), пусть x1 и x2 - две его вершины. Длина кратчайшего (x1, x2 ) - маршрута называется расстоянием между вершинами x1 и x2 обозначается через d(x1 , x2 ). Очевидно, что расстояние между вершинами является простой
цепью и d(xi , xi )= 0 . Для любой вершины x величина |
|
||
e(x) = max d(x, y) |
(1.13.6) |
||
|
y S |
|
|
называется эксцентриситетом вершины |
x . |
Максимальный |
из всех эксцентриситетов |
вершин называется диаметром графа и обозначается d(G), т. е. |
|
||
d(G) = max e(x) = max max d (x, y). |
(1.13.7) |
||
x S |
x S |
y S |
|
Минимальный из эксцентриситетов вершин графа называется его радиусом и обозначается
через r(G): |
r(G)= min e(x)= min max d(x, y). |
(1.13.8) |
|
|
x S |
x S y S |
|
Вершина x называется периферийной, если ее эксцентриситет равен диаметру графа, т. е. e(x) = d (G). Простая цепь, расстояние между концами которой равно d(G), называется
диаметральной цепью.
|
x6 |
Вершина |
x |
называется |
центральной, |
|
если |
|
|
e(x) = r(G). |
||||||
|
Множество всех центральных вершин графа называется его центром. |
|||||||||||||||
x5 |
|
|||||||||||||||
|
Центром |
может |
быть |
единственная |
вершина графа или |
несколько |
||||||||||
|
x7 |
|||||||||||||||
|
вершин |
(см. |
рис. |
1.15). |
Здесь |
e(x ) = e(x |
2 |
) = e(x |
4 |
)= e(x |
6 |
) = 3, |
||||
|
|
e(x3 ) = e(x7 )= 4 , |
|
|
|
|
1 |
|
|
|
|
|||||
x3 |
x4 |
|
|
|
|
|
|
|
|
|
|
|
|
|||
e(x5 ) = 2 . Таким образом, d(G) = 4, |
r(G) = 2 . Периферийные вершины |
|||||||||||||||
Рис. 1.15 |
||||||||||||||||
x3 и x7 , |
диаметральные цепи: x3 - x2 - x5 - x6 - x7 |
и |
x3 - x2 - x5 - x6 - x7 , |
|
центральная |
|||||||||||
вершина x5 .
1.13.4. Релейно-контактные (переключательные) схемы. Рассмотрим еще один способ реализации функций алгебры логики – релейно-контактные схемы (РКС), широко используемые в электронно-вычислительной технике. Описание и конструирование таких схем в силу их громоздкости весьма затруднительно. Однако оказалось, что при конструировании РКС можно использовать аппарат булевых функций.
Исходное замечание состоит в том, что если логической переменной x поставить в соответствие проводник, по которому ток идет или нет в зависимости от того x = 1 или x = 0, то последовательному соединению проводников отвечает конъюнкция переменных, а параллельному – дизъюнкция. Часто проводники на схемах заменяют обозначением специальных устройств – переключателей, которые могут быть механическими и электронными. Многократно используя параллельно-последовательные соединения, можно строить сложные схемы. Мы ограничимся только схемами, в которых соединяются лишь контакты. Контакт или переключатель будем изображать отрезком или прямоугольником, концы контакта называть полюсами. Конструкция, изображенная на рис. 1.16, называется двухполюсником. Двухполюсник будем снабжать символом переменной x , если контакт
41

|
замыкающий, |
и x , если |
размыкающий. Двухполюсники |
соединяются |
||||||||||||||
|
полюсами. В результате схема будет представлять из себя граф. |
|||||||||||||||||
|
|
Граф Γ с k |
полюсами, в котором каждое ребро помечено буквой |
|||||||||||||||
|
из |
алфавита |
X n |
= {x , x |
|
,..., x |
|
, |
|
, |
|
|
,..., |
|
|
}, |
называется |
k -полюсной |
|
2 |
n |
x |
x |
2 |
x |
n |
|||||||||||
|
|
|
|
1 |
|
1 |
|
|
|
|
|
|
|
|||||
Рис 1.16 |
контактной |
схемой, реализующей булевы функции переменных |
||||||||||||||||
x1, x2 ,..., xn , или |
k, n |
-схемой. |
Контактная |
схема |
называется |
связной (сильно связной, |
||||||||||||
паралллельно-последовательной), если таковым является ее граф. Параллельно- последовательная схема называется π -схемой. В графе выделяются две вершины: вход и выход. Часто вход изображает полюс в виде светлого кружка, остальные полюса изображаются темными кружками.
Какую же функцию алгебры логики реализует контактная схема? Эта функция равна единице при тех значениях аргументов, при которых в схеме есть проводимость, и нулю, если проводимости нет. Пусть a и b - два полюса контактной схемы Σ , [a,b] - некоторая
цепь, соединяющая a и b , и K[a,b] - конъюнкция букв, приписанных ребрам цепи [a,b].
~ |
|
|
|
|
|
|
|
Функция fa,b (x |
n |
), определяемая формулой |
|
|
|
|
|
|
|
|
|
|
|||
|
|
~ |
|
|
|
|
|
|
|
fa,b (x |
n |
)= |
|
K[a,b], |
(1.13.9) |
|
|
|
|||||
|
|
|
|
|
[a,b] |
|
|
в которой дизъюнкция берется по всем простым цепям схемы, соединяющим полюса a и b , называется функцией проводимости между полюсами a и b схемы Σ . На самом деле для получения функции проводимости достаточно брать дизъюнкцию не по всем цепям, а лишь по некоторым.
Цепь Γ1 называется существенной, если она ни через какую вершину графа не проходит дважды. Оказывается, что дизъюнкция конъюнкций, соответствующих существенным цепям, равносильна функции проводимости. Действительно, пусть имеется некоторая цепь, в которой некоторая вершина встречается дважды. Отбросим все контакты, которые встречаются между двумя прохождениями через эту вершину. Ясно, что при этом мы вновь получим цепь, причем если все контакты исходной цепи были замкнуты, то будут замкнуты и все контакты вновь полученной цепи. Таким образом, последовательно сокращая цепь, можно получить существенную цепь, в которой будет проводимость, если была проводимость в исходной цепи.
|
Посмотрим теперь как обстоит дело с обратной задачей: построением по функции |
|||||||||||||
|
y1 |
y2 |
yk |
реализующей ее схемы. Представим функцию в виде ДНФ. |
||||||||||
|
|
|
… |
Каждой |
входящей |
в |
ДНФ |
элементарной |
конъюнкции |
|||||
|
|
|
|
|||||||||||
|
|
Рис. 1.17 |
|
xσ1 xσ2 |
... xσk |
поставим |
в соответствие |
схему (рис. |
||||||
|
|
|
|
1 |
2 |
|
k |
|
|
|
|
|
|
|
|
|
y1 |
|
1.17), состоящую из последовательно соединенных |
||||||||||
|
|
y |
|
контактов |
xσ1 , xσ2 |
,..., xσk . |
Это |
схема |
элементарной |
|||||
|
|
2 |
|
|
|
|
1 |
2 |
|
k |
|
|
|
|
|
|
|
|
конъюнкции. На рис. 1.17 и 1.18 величины xσi |
обозначены |
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
i |
|
|
|
... |
|
через |
yi |
. |
После |
отождествления |
между |
собой, с одной |
||||
|
|
|
стороны, |
|
входов |
всех этих |
схем, с другой |
стороны – |
||||||
|
|
yk |
|
|
||||||||||
|
|
|
выходов, получим функцию, соответствующую заданной |
|||||||||||
|
|
|
|
|||||||||||
|
|
Рис.1.18 |
|
схеме. Естественно, можно реализовать функцию по схемам |
||||||||||
xσ1 |
xσ2 |
... xσk |
|
также исходя из КНФ. Каждой элементарной дизъюнкции |
||||||||||
поставим |
в соответствие схему, |
изображенную на |
рис. 1.18. Затем |
|||||||||||
1 |
2 |
k |
|
|
|
|
|
|
|
|
|
|
|
|
последовательно соединим все эти схемы для всех элементарных дизъюнкций, входящих в КНФ, так, чтобы вход последующей схемы совпадал с выходом предыдущей.
Схему, состоящую из одного контакта, называют элементарной. Ясно, что любая π -
схема может быть получена из элементарных за некоторое число шагов при помощи параллельных и последовательных соединений. Каждому способу построения π -схемы из
42

элементарных схем отвечает представление функции проводимости в виде формулы, содержащей только дизъюнкции, конъюнкции и отрицания.
Если контактная схема является π -схемой, то ее можно разбить на несколько схем, соединенных либо последовательно, либо параллельно. Обратное тоже верно. Если схема не допускает разбиения на две схемы, соединенные либо последовательно, либо параллельно, она не является π -схемой. Для примера рассмотрим схему “мостик” (рис. 1.19), которая не является элементарной. Если две схемы соединены последовательно, то у полученной общей схемы все полюсы, кроме соединяющего, либо не имеют общих контактов ни с входом, ни с
выходом всей схемы, либо имеют общий контакт или только с входом,
x |
y |
или только с выходом. Очевидно, что какой бы из внутренних полюсов |
|
z |
|
на рис. 1.19 мы не приняли за соединяющий подсхемы, оставшийся |
|
|
полюс будет иметь общий контакт как с входом, так и с выходом схемы. |
||
|
|
||
t |
u |
Поэтому схему “мостик” нельзя получить последовательным |
|
соединением двух схем. |
|||
|
|
||
|
|
Если общая схема – результат параллельного соединения двух |
|
Рис. 1.19 |
|
схем, то ее контакты и полюсы можно разбить на две части так, чтобы |
либо в одной части содержались контакты, непосредственно соединяющие вход и выход, либо полюсы, входящие в рассматриваемые различные две части схемы и отличные от входа и выхода, не будут иметь общих контактов. Ни первая, ни вторая возможность на схеме рис. 1.19 не может реализоваться. Следовательно, эта схема не
|
является π -схемой. |
|
x2 |
Две контактные схемы называются эквивалентными, |
|
если они реализуют одну и ту же булеву функцию или одну и |
||
б |
||
а |
ту же систему функций. Схема называется минимальной, если |
|
|
||
x2 |
она содержит наименьшее возможное число контактов среди |
|
x2 в |
всех схем, имеющих ту же функцию проводимости. |
|
Пример 3. Найти функции, реализуемые схемами на |
||
Рис. 1.20 |
рис. 1.20. |
|
Первые две функции представлены π -схемами, поэтому их |
||
|
восстановление довольно просто: а) f (x1, x2 )= x1 x2 x1x2 ; б) f (x1, x2 )= (x1 x2 ) (x1 x2 ).
Для последнего пункта (в) составим по формуле (1.12.9) функцию проводимости. Для этого необходимо перечислить все цепи, соединяющие начальный a и конечный b полюсы
|
~2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
схемы: |
) = f (x1 |
, x2 ) = K[a,b] = x1 x2 |
x1 x2 |
x2 x3 x2 x2 x3 x2 x1 x3 x3 x2 |
x1 x3 x2 x2 |
≡ |
||||||||||||||
fa,b (x |
||||||||||||||||||||
|
|
|
[a,b] |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
≡x1 x2 x1x2 x2 x3 .
1.14.Практическое занятие № 2. Математические основы информатики. Алгебра высказываний. Операции над множествами. Графы и
способы задания графов. Релейно-контактные схемы
Основное понятие алгебры логики – высказывание. Основные понятия любой отрасли науки не могут быть определены строго формально, а лишь поясняются. Логическое значение высказывания “истина” (“ложь”) чаще всего обозначаются цифрой 1 (0). Все высказывания можно разделить на простые и составные или сложные. Логическое значение
любого высказывания легко может быть установлено с помощью таблиц истинности основных логических операций.
Пример 1. Определить являются ли высказываниями следующие предложения, и установить истинность или ложность имеющихся высказываний:
1.число 15 не делится на 3;
2.летайте самолётами Аэрофлота!
3.есть ли жизнь на Марсе?
4.в Петербурге более 4-х миллионов жителей;
5.все действительные числа удовлетворяют коммутативному закону.
43

Из приведённых пяти предложений второе и третье не являются высказываниями, т. к. высказыванием может быть лишь повествовательное предложение. Первое
высказывание ложно, четвертое и пятое – истинны. |
|
|
|
||||||||
Пример |
2. |
Составить |
таблицу |
истинности |
для |
формулы |
|||||
f (x1, x2 , x3 )= (x1 → |
|
)→ ( |
|
|
|
). |
|
|
|
|
|
x2 |
x1 x2 |
x3 |
|
|
|
|
|||||
Применение |
таблицы истинности – |
самый |
простой способ |
исследования |
булевой |
||||||
функции. Каждая таблица для функции n переменных содержит 2n строк, поэтому таблицы истинности удобно применять, если функция содержит не более 3-4-х переменных. В нашем
случае
Таблица 1.19
x1 |
x2 |
x3 |
|
|
|
|
x → |
|
|
|
x1 x2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
f |
x |
2 |
x |
2 |
x x |
2 |
x |
x x |
2 |
x |
3 |
||||||||||||||||
|
|
|
|
|
|
1 |
|
|
|
|
1 |
|
3 |
|
1 |
|
|
|
|
|||||||
1 |
1 |
1 |
|
0 |
|
0 |
|
|
|
1 |
|
0 |
|
|
0 |
|
0 |
|
|
|
|
1 |
||||
1 |
1 |
0 |
|
0 |
|
0 |
|
|
|
1 |
|
0 |
|
|
1 |
|
0 |
|
|
|
|
1 |
||||
1 |
0 |
1 |
|
1 |
|
1 |
|
|
|
1 |
|
0 |
|
|
0 |
|
0 |
|
|
|
|
0 |
||||
1 |
0 |
0 |
|
1 |
|
1 |
|
|
|
1 |
|
0 |
|
|
1 |
|
0 |
|
|
|
|
0 |
||||
0 |
1 |
1 |
|
0 |
|
1 |
|
|
|
1 |
|
0 |
|
|
0 |
|
0 |
|
|
|
|
0 |
||||
0 |
1 |
0 |
|
0 |
|
1 |
|
|
|
1 |
|
0 |
|
|
1 |
|
0 |
|
|
|
|
0 |
||||
0 |
0 |
1 |
|
1 |
|
1 |
|
|
|
0 |
|
1 |
|
|
0 |
|
0 |
|
|
|
|
0 |
||||
0 |
0 |
0 |
|
1 |
|
1 |
|
|
|
0 |
|
1 |
|
|
1 |
|
1 |
|
|
|
|
1 |
||||
По табл. 1.19 видно, что формула f (x1, x2 , x3 ) - выполнима, т. к. принимает значения 0 и 1 при разных наборах переменных x1, x2 , x3 .
Пример 3. Доказать, что если формулы P Q и R Q тождественно истинны, то
формула P → |
R |
также тождественно истинна. |
|
P =1, |
|
= 0 , т. е. |
||||||||||||||
Предположим обратное, пусть P → |
|
= 0 . Тогда из таблицы 1.16 |
|
|||||||||||||||||
R |
R |
|||||||||||||||||||
R =1. Следовательно, |
|
Q = 1 Q = 0 Q = 1 и |
|
|
|
= 0 |
|
= 1, |
т. е. |
Q = 1 |
и |
|
= 1 |
|||||||
P |
R |
Q |
Q |
Q |
||||||||||||||||
одновременно, что невозможно. Таким образом, наше предположение неверно и P → |
|
= 1. |
||||||||||||||||||
R |
||||||||||||||||||||
Пример 4. Булевы функции, представленные по формулам |
(1.13.4) и |
(1.13.5), |
||||||||||||||||||
находятся в виде совершенных дизъюнктивной и конъюнктивной нормальных форм. К
такому виду любую булеву функцию можно привести путём эквивалентных преобразований с использованием формул (1.13.1)-(1.13.3). Однако самый простой, но не самый удобный способ – использование таблицы истинности.
По структуре формулы (1.13.4) ясно, что в её правой части стоят логические слагаемые, каждое из которых состоит из логического произведения всех переменных исходной формулы или их отрицаний, причём только из тех строк таблицы истинности, в
которых сама функция равна единице. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
Поэтому, чтобы получить совершенную дизъюнктивную нормальную форму булевой |
|||||||||||||||||||||||||||||
функции |
f (x1, x2 ,...,xn ), необходимо записать в |
виде дизъюнкции все выражения вида |
||||||||||||||||||||||||||||
xσ1 |
xσ2 |
... xσn только в тех строках таблицы истинности, где f (σ |
,σ |
2 |
,...,σ |
n |
)=1. |
|
|
|
||||||||||||||||||||
1 |
2 |
n |
1 |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
Рассмотрим в качестве примера функцию |
f (x, y, z)= (x |
|
)→ y z |
|
|
и её таблицу |
|||||||||||||||||||||||
|
z |
|
|
|||||||||||||||||||||||||||
истинности 1.20. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
Тогда СДНФf = xyz |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
xyz x yz . Форму (1.13.5) удобнее получать не напрямую, а по |
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
формуле |
СКНФf = |
СДНФ |
|
. В нашем случае |
СДНФ |
|
= xy |
|
x |
|
|
|
|
|
|
|
|
|
|
|
||||||||||
f |
f |
z |
yz x yz xyz x yz и |
|||||||||||||||||||||||||||
СКНФf = xyz xyz x yz xyz x yz ≡ xyz x yz x yz xyz x yz ≡ (x y z) (x y z)(x y z) (x y z) (x y z).
44

|
|
|
|
|
|
|
|
|
|
|
Таблица 1.20 |
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
y |
z |
|
z |
|
x Ú |
z |
|
y z |
f |
|
|
f |
|
1 |
1 |
1 |
|
0 |
1 |
|
|
1 |
1 |
|
0 |
|
||
1 |
1 |
0 |
|
1 |
1 |
|
|
0 |
0 |
|
1 |
|
||
1 |
0 |
1 |
|
0 |
1 |
|
|
0 |
0 |
|
1 |
|
||
1 |
0 |
0 |
|
1 |
1 |
|
|
0 |
0 |
|
1 |
|
||
0 |
1 |
1 |
|
0 |
0 |
|
|
1 |
1 |
|
0 |
|
||
0 |
1 |
0 |
|
1 |
1 |
|
|
0 |
0 |
|
1 |
|
||
0 |
0 |
1 |
|
0 |
0 |
|
|
0 |
1 |
|
0 |
|
||
0 |
0 |
0 |
|
1 |
1 |
|
|
0 |
0 |
|
1 |
|
||
Алгебра логики и теория множеств являются двумя интерпретациями (моделями) одной общей теории, называемой алгеброй Буля . Поэтому все понятия алгебры логики и теории множеств очень похожи.
Пример 5. Доказать равенство A Ç (B \ A)= Æ . Проще всего это сделать с помощью диаграмм Эйлера – Венна (см. рис. 1.21). Видно, что
Uмножества A и B \ A непересекающиеся, т. е. не имеют общих элементов. То же самое можно полу-
A |
B |
|
чить чисто формально: B \ A = B Ç |
A |
(см. рис. 1.21), |
||||||
|
|
|
A Ç (B \ A)= A Ç (B Ç |
|
)= A Ç |
|
Ç B = Æ Ç B = Æ . |
||||
|
|
|
A |
A |
|||||||
|
|
|
Пример |
6. Пусть A = {1,2,3,4}, B = {4,5,6}. |
|||||||
|
|
|
Найти AÇ B , AÈ B , A \ B , |
AÅ B , A´ B , B ´ A . |
|||||||
|
|
B\A |
AÇ B = {4}, |
AÈ B = {1,2,3,4,5,6}, |
A \ B = {1,2,3}, |
||||||
Рис. 1.21 |
A Å B = (A \ B)È (B \ A)= {1,2,3}È{5,6}= {1,2,3,5,6}, |
||||||||||
|
|
|
|||||||||
A´ B = {(1,4),(1,5),(1,6),(2,4),(2,5),(2,6),(3,4),(3,5),(3,6),(4,4),(4,5),(4,6)}, |
|
B ´ A = {(4,1),(4,2),(4,3), |
|||||||||
(4,4),(5,1),(5,2),(5,3),(5,4),(6,1),(6,2),(6,3),(6,4)}, очевидно A´ B ¹ B ´ A . |
|
|
|
|
|
||||||
Пример 7. |
Дано |
бинарное отношение P Í A2 , A = {1,2,3,4}, |
|
изображённое на рис. |
|||||||
1. 22. Определить является ли оно рефлексивным, иррефлексивным, симметричным, антисимметричным, транзитивным?
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
æ |
1 |
1 |
0 |
0 |
ö |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ç |
0 |
0 |
0 |
0 |
÷ |
|
|
|
Матрица |
|
этого |
|
|
отношения |
имеет вид |
|
P |
|
ç |
÷ |
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||
1 |
2 |
|
|
|
|
|
|
= ç |
0 |
0 |
1 |
0 |
÷ . |
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ç |
÷ |
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ç |
0 |
1 |
1 |
0 |
÷ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
è |
ø |
||||
4 |
3 |
Отношение P не рефлексивно, т. к. на главной диагонали его матрицы |
||||||||||||||||||||||||||||||||||||||||||
|
|
имеется два нуля; это отношение не иррефлексивно, т. к. |
p11 = p33 =1. |
|||||||||||||||||||||||||||||||||||||||||
Рис. 1.22 |
|
Матрица |
|
P |
|
не симметрична, тогда не симметрично и отношение P ; |
||||||||||||||||||||||||||||||||||||||
|
|
|
||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||
для симметричных отношений справедливо |
|
P |
|
|
|
T = |
|
|
|
P |
|
|
|
, |
что, |
очевидно, |
|
не выполняется в |
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
æ |
1 1 0 0ö |
æ |
1 1 0 0ö æ |
1 |
0 |
0 |
0ö |
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ç |
0 0 0 0 |
÷ |
ç |
0 0 0 0 |
÷ |
ç |
0 |
0 |
0 |
0 |
÷ |
||||||||||||||||
данном |
случае. |
|
P Ç P−1 |
|
= |
|
P |
|
* |
|
P |
|
T |
ç |
÷ |
ç |
÷ ç |
÷ |
||||||||||||||||||||||||||
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
= ç |
0 0 1 0 |
÷*ç |
0 0 1 0 |
÷ |
= ç |
0 |
0 |
1 |
0 |
÷ . |
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ç |
÷ |
ç |
÷ ç |
÷ |
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ç |
0 1 1 0 |
÷ |
ç |
0 1 1 0 |
÷ |
ç |
0 |
0 |
0 |
0 |
÷ |
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
è |
ø |
è |
ø è |
ø |
|||||||||||||||||||||||
Джордж Буль (1815-1864) – английский математик и логик.
45

Отношение |
P |
антисимметрично, |
т. к. все |
элементы, |
стоящие вне |
|
главной диагонали |
||||||||||||||||||||||||||||||||
матрицы |
|
P Ç P−1 |
|
|
|
|
, равны нулю. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
Транзитивность проще проверить по определению, используя элементы этого |
|||||||||||||||||||||||||||||||||||||
отношения: P = {(1,1),(1,2),(4,2),(4,3),(3,3)}. По определению отношение P транзитивно, если |
|||||||||||||||||||||||||||||||||||||||
из (x, y)Î P и |
(y, z)Î P следует, что |
(x, z)Î P . |
В нашем случае |
|
(1,1)Î P , |
|
(1,2)Î P , |
но и |
|||||||||||||||||||||||||||||||
(1,2)Î P ; (4,3)Î P , |
(3,3)Î P , но и (4,3)Î P , т. е. P транзитивно. |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
|
Пример 8. Для графов, изображённых на рис. 1.23, составить матрицу смежности |
|||||||||||||||||||||||||||||||||||||
вершин и инциденций. |
x2 |
|
|
|
|
|
|
|
|
|
x1 |
|
u1 |
|
x2 |
|
x3 |
|
|
|
x4 |
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
а) |
|
|
|
|
|
x4 |
|
|
|
б) |
|
|
|
u8 |
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
u1 |
|
u2 |
|
|
|
|
|
u7 |
|
|
|
|
|
|
u2 |
|
|
|
u5 |
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
u3 |
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
u5 |
u6 |
|
|
x6 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
x1 |
|
|
|
|
|
|
|
|
u9 |
|
|
|
|
|
|
|
|
|
|
|
u |
|
|
u11 |
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
u3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
9 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
u8 |
x5 |
|
|
|
|
|
|
|
|
|
|
|
u6 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x3 |
|
|
|
|
|
|
|
|
|
|
x7 |
|
|
x6 |
|
|
x5 |
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Рис. 1.23 |
|
|
|
|
|
|
u7 |
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
а) Дан ориентированный граф. Тогда |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
x1 |
|
x2 |
x3 |
x4 |
x5 |
x6 |
|
|
|
|
u u |
2 |
u |
3 |
u |
4 |
u |
5 |
u |
6 |
u |
7 |
u |
8 |
u |
9 |
u |
|
|||||||||
x1 |
æ |
0 |
1 0 1 1 0ö |
|
|
x |
|
1 |
|
|
|
|
|
|
|
|
10 |
||||||||||||||||||||||
|
|
æ 1 1 |
1 0 |
|
0 0 |
|
0 0 |
0 0ö |
|||||||||||||||||||||||||||||||
x2 |
ç |
0 |
0 1 1 0 0 |
÷ |
|
|
1 |
ç |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
÷ |
||||||||||||
ç |
÷ |
|
|
x2 |
ç |
-1 0 |
0 1 |
|
1 0 |
|
0 0 |
0 0 |
÷ |
||||||||||||||||||||||||||
P = x3 |
ç |
0 |
0 |
|
|
|
|
|
0 |
1 0 0 |
÷ |
и R = x3 |
ç |
0 0 |
0 |
0 -1 1 |
|
0 -1 0 |
0 |
÷ |
|||||||||||||||||||
ç |
|
|
|
|
|
÷ |
ç |
|
÷. |
||||||||||||||||||||||||||||||
x4 |
ç0 0 |
|
|
|
|
|
0 |
0 0 1÷ |
|
|
x4 |
ç 0 -1 0 -1 |
|
0 -1 1 0 -1 |
0÷ |
||||||||||||||||||||||||
x5 |
ç |
0 |
0 1 1 0 1 |
÷ |
|
|
x |
ç |
0 0 -1 |
0 |
|
0 0 0 1 1 1 |
÷ |
||||||||||||||||||||||||||
|
|
ç |
|
|
|
|
|
|
|
|
|
|
|
|
÷ |
|
|
5 |
ç |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
÷ |
|
x6 |
ç |
0 |
0 0 |
0 0 0 |
÷ |
|
|
x6 |
ç |
0 0 0 |
0 |
|
0 0 -1 0 0 -1 |
÷ |
|||||||||||||||||||||||||
è |
ø |
|
|
è |
|
ø |
|||||||||||||||||||||||||||||||||
|
|
б) Этот граф неориентированный, поэтому матрица смежности вершин будет |
|||||||||||||||||||||||||||||||||||||
симметрической, а матрица инциденций – бинарной. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
x |
|
|
x1 |
x2 |
|
x3 |
x4 |
x5 |
|
x6 |
x7 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
æ0 |
1 |
|
|
|
|
|
0 |
0 |
0 |
|
0 |
1ö |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
1 |
|
ç |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
÷ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x2 |
ç |
1 |
0 0 0 |
0 |
|
0 1 |
÷ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
P = |
x |
ç |
0 |
0 |
|
|
|
|
|
0 |
1 |
0 |
|
0 |
1 |
÷ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
3 |
|
ç |
|
|
0 1 0 |
1 |
|
|
|
÷, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
x4 |
ç0 |
|
1 1÷ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
x5 |
ç |
0 |
0 0 1 |
0 |
|
1 1 |
÷ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
ç |
|
÷ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
x6 |
ç |
0 |
0 0 1 |
1 |
|
0 1 |
÷ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
x7 |
ç |
1 |
1 1 1 |
1 |
|
1 0 |
÷ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
è |
|
ø |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
x |
|
u1 u2 |
u3 |
u4 |
u5 |
|
u6 |
u7 |
u8 |
|
u9 |
u10 |
u11 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
æ1 1 0 0 0 0 0 0 0 0 0ö |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
1 |
|
ç |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
÷ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x2 |
ç |
1 0 1 0 0 0 0 0 0 0 0 |
÷ |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
R = |
x |
ç |
0 0 0 1 0 0 0 1 0 0 0 |
÷ |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
3 |
|
ç |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
÷. |
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
x4 |
ç0 0 0 0 1 0 0 1 1 0 1÷ |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
x |
ç |
0 0 0 0 0 0 1 0 0 1 1 |
÷ |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
5 |
|
ç |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
÷ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x6 |
ç |
0 0 0 0 0 1 0 0 1 1 0 |
÷ |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
x7 |
ç |
0 1 1 1 1 1 1 0 0 0 0 |
÷ |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
è |
ø |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
46

|
Пример 9. По данной матрице смежности вершин |
P и инциденций |
R нарисовать |
|||||||||||||||||||||||
соответствующий граф. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
æ |
1 2 0 2ö |
|
æ1 1 0 1 0 1 0 |
ö |
|
|
|
|
|
|
||||||||||||||||
ç |
0 1 0 1 |
÷ |
|
ç |
0 1 1 0 1 0 1 |
÷ |
|
|
|
|
|
|
||||||||||||||
ç |
÷ |
|
ç |
÷ |
|
|
|
|
|
|
||||||||||||||||
P = ç |
0 1 0 1 |
÷ |
, |
R = ç |
0 0 1 1 1 1 0 |
÷ . |
|
|
|
|
|
|
||||||||||||||
ç |
÷ |
|
ç |
÷ |
|
|
|
|
|
|
||||||||||||||||
ç |
0 0 1 0 |
÷ |
|
ç |
1 0 0 0 0 0 1 |
÷ |
|
|
|
|
|
|
||||||||||||||
è |
ø |
|
è |
ø |
|
|
|
|
|
|
||||||||||||||||
|
По первой матрице P может быть построен ориентированный мульти- и псевдограф, |
|||||||||||||||||||||||||
|
|
|
|
|
|
изображённый на рис. 1.24. Следует помнить, что рисунок графа |
||||||||||||||||||||
|
|
x2 |
|
|
|
может быть и иным по расположению вершин и форме дуг, важно |
||||||||||||||||||||
|
|
|
|
|
лишь количество вершин и дуг и порядок их инцидентности. Так как |
|||||||||||||||||||||
|
|
|
|
|
|
|||||||||||||||||||||
x1 |
|
|
|
|
x4 |
матрица |
R |
бинарна, |
|
то ей |
соответствующий |
граф будет |
||||||||||||||
|
|
|
|
|
|
неориентированным. Он изображён на рис. 1.25. |
|
|||||||||||||||||||
|
|
x3 |
|
|
|
|
|
|
|
Пример 10. Найти эксцентриситет вершин, радиус и диаметр |
||||||||||||||||
|
|
|
|
|
|
графа, изображённого на рис. 1.25. |
|
|
||||||||||||||||||
|
|
Рис. 1.24 |
|
|
|
|
|
|
|
e(x1 )= e(x2 )= e(x3 )= e(x4 )= 3 , r(G)= d(G)= 3. |
Все вершины |
|||||||||||||||
|
|
x2 |
|
|
|
|
|
|
|
|||||||||||||||||
x1 |
|
|
|
центральные и периферийные. Диаметральные цепи: |
|
|||||||||||||||||||||
|
u5 |
u7 |
|
x1 - x4 - x2 - x3 , x2 - x3 - x1 - x4 , x3 - x1 - x4 - x2 , |
|
|||||||||||||||||||||
|
|
u3 |
|
x4 x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
4 |
- x |
2 |
- x - x , x |
4 |
- x - x |
2 |
- x и т. п. |
|
||||||||||||||
|
u2 |
u6 |
|
|
|
|
|
3 |
1 |
|
|
|
|
|
|
1 |
|
|
3 |
|
|
|||||
|
|
|
|
|
|
|
|
Пример |
11. |
|
|
|
Реализовать |
релейно-контактными схемами |
||||||||||||
|
u1 |
x3 |
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
функции: а) |
f (x, y, z)= (x ® (y ® z))® (y ® x); |
|
||||||||||||||||||||
|
Рис. 1.25 |
|
|
|
||||||||||||||||||||||
|
|
|
б) |
f (x, y, z)= xyz Ú |
|
|
|
|
|
|
Ú |
|
|
|
|
|
|
|||||||||
|
|
|
|
|
x |
|
y |
|
z |
xy . |
|
|
||||||||||||||
Поскольку релейно-контактные схемы реализуются на основе элементарных конъюнкции и дизъюнкции, то при необходимости следует упростить формулу по правилам
(1.13.1)-(1.13.3).
а) f (x, y, z) = (x ® (y ® z)) ® (y ® x) º (x Ú (y Ú z))Ú (y Ú x)º (x Ù (y Ú z))Ú y Ú x º
º x Ù (y Ù z)Ú y Ú x º xyz Ú y Ú x º x(1Ú yz)Ú y º x Ú y . Тогда релейно-контактная схема имеет вид, изображённый на рис. 1.26 а).
|
|
|
y |
|
а) |
|
|
|
|
z |
|
x |
|
|
|
x |
|
y |
б) x |
x t |
y |
||
б) x |
|
|
z |
|
|
||||||
|
x |
y |
|
|
|
z |
|
y |
|
||
y |
|
z |
|
|
x |
|
|
|
|||
|
|
|
|
|
|
z |
y |
t |
|
||
|
|
x |
|
y |
|
|
|
x |
|||
|
|
|
|
y |
|
|
|||||
|
|
|
|
|
|
z |
|||||
|
|
|
|
|
|
|
|
Рис. 1.27 |
|
||
|
Рис. 1.26 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
б) В этом случае формулу упрощать не требуется. Релейно-контактная схема этой формулы изображена на рис. 1.26 б).
Пример 12. Найти функции, реализуемые релейно-контактными схемами, изображёнными на рис. 1.27.
а) f (x, y, z)= x Ù y Ú z Ú (x Ú y)Ù z º x y Ú z Ú xz Ú yz º z(1Ú x Ú y)Ú xy º z Ú x y ;
б) f (x, y, z)= (x Ù (z Ú x Ù t)Ù y)Ú ((y Ù t Ú y Ù z)Ù x)º x yz Ú x yt Ú x yt Ú x yz º yt(x Ú x)Ú
Úyz(x Ú x)º yt Ú yz º y(t Ú z).
1.14.1.Обозначить элементарные высказывания буквами и записать следующие высказывания с помощью символов алгебры логики:
а) 5 < 20 или π R ;
б) если число 512 делится на 2 и 8, то оно делится на 16; в) тает лёд и e < π .
47

1.14.2. Пусть высказывание pk = { мишень поражена k -м выстрелом }, k =1,2,3 . Что означают следующие высказывания:
а) p1 Ú p2 Ú p3 ; б) p1 Ù p2 Ù p3 ; в) (p1 Ú p2 )Ù p3 ?
1.14.3.Составить таблицы истинности для формул:
а) f (x1, x2 ,...,xn )= x1 ® (x2 ® (... ® xn )...);
б) f (x, y)= (x ® y)® (y ® x);
в) f (x, y)= ((x Ù y)® y)® (x ® y).
1.14.4.По таблице истинности получить СДНФ и СКНФ для формул:
а) f (x, y, z)= (xy ® yz)® ((x ® y)® (z ® y));
б) f (x, y)= x y ® (y ® x);
в) f (x, y, z)= (z ® x)® ((y Ú z)® x).
1.14.5. Доказать следующие тождества:
а) A \ (B ÇC)= (A \ B)È (A \ C); б) A È B = A È (B \ A);
в) A \ (B \ C)= (A \ B)È (A ÇC).
1.14.6. Определить в каком отношении ( X Ì Y , X É Y, X = Y ) находятся множества
X и Y , если:
а) X = AÈ (B \ C),Y = (AÈ B)\ (A ÈC);
б) X = A \ (B ÈC), Y = (A \ B)È (A \ C);
в) X = (A´ B)È (C ´ B),Y = (A È C)´ B .
1.14.7. По данной матрице смежности вершин |
P |
или инциденций |
R |
|
построить |
||||||||||||||||
соответствующий граф: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
æ0 |
1 |
0 |
1 |
1 |
1 |
ö |
æ |
1 1 1 |
|
0 0 0 0 0 0 ö |
|
|||||||||
|
ç |
1 |
0 |
0 |
1 |
1 |
1 |
÷ |
|
|
|||||||||||
|
ç |
÷ |
ç |
0 0 0 |
|
1 1 0 0 -1 |
0 |
÷ |
|
||||||||||||
|
ç |
0 |
0 0 1 0 1 |
÷ |
ç |
|
÷ |
|
|||||||||||||
а) P = |
ç |
÷ |
; б) R = ç |
0 |
|
0 -1 0 -1 1 1 0 |
0 |
÷ |
; |
||||||||||||
|
ç1 |
1 |
1 |
0 |
0 |
0 |
÷ |
ç |
|
|
|
|
|
|
|
|
|
|
÷ |
|
|
|
ç |
1 |
1 |
0 |
0 |
0 |
0 |
÷ |
ç |
0 -1 0 0 0 0 -1 1 1 ÷ |
|
||||||||||
|
ç |
÷ |
ç |
|
|
|
|
|
|
|
|
|
|
÷ |
|
||||||
|
ç |
1 |
1 |
1 |
0 |
0 |
0 |
÷ |
è |
-1 0 0 -1 0 -1 0 0 -1ø |
|
||||||||||
|
è |
ø |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
æ0 |
1 |
1 |
0 |
1 |
0 |
ö |
æ |
1 |
1 |
0 |
0 |
0 |
0 |
0 |
0ö |
|
|
|
||
|
ç |
0 |
0 |
0 |
1 |
1 |
1 |
÷ |
|
|
|
||||||||||
|
ç |
÷ |
ç |
0 |
1 |
1 |
1 |
1 |
0 |
0 |
0 |
÷ |
|
|
|
||||||
|
ç |
0 1 0 1 1 0 |
÷ |
ç |
÷ |
|
|
|
|||||||||||||
в) P = |
ç |
÷ |
; г) R = ç |
0 |
0 |
0 |
0 |
1 |
1 |
0 |
1 |
÷ . |
|
|
|
||||||
|
ç0 |
0 |
0 |
0 |
1 |
1 |
÷ |
ç |
0 |
0 |
1 |
0 |
0 |
0 |
1 |
|
÷ |
|
|
|
|
|
ç |
0 |
0 |
0 |
0 |
0 |
1 |
÷ |
ç |
1÷ |
|
|
|
||||||||
|
ç |
÷ |
ç |
1 |
0 |
0 |
1 |
0 |
1 |
1 |
0 |
÷ |
|
|
|
||||||
|
ç |
0 |
0 |
1 |
0 |
0 |
0 |
÷ |
è |
ø |
|
|
|
||||||||
|
è |
ø |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
1.14.8.Для графов, изображённых на рис. 1.28, составить матрицы смежности вершин
иинциденций:
48

а) |
x2 |
u6 |
x3 |
|
б) |
x1 |
u3 |
x2 |
u6 x3 |
x4 |
в) |
x1 |
u3 |
x2 |
|
x3 |
|
u3 |
|
|
|
|
|
|
|
u8 |
|
|
|
|
|
||
x1 |
u5 |
u7 u8 |
u9 |
|
u1 |
u2 |
u5 |
u7 |
|
u1 |
u2 |
|
|
|
||
u2 |
|
x6 |
|
u9 |
|
u9 |
u6 |
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
u5 |
|
||
|
u1 |
|
|
u12 |
|
|
|
|
|
|
|
u |
|
x4 |
||
|
|
u11 |
|
x8 |
u12 |
x7 |
x6 u11 x5 |
|
x6 |
x5 |
|
|||||
|
|
|
|
|
|
8 |
|
|
||||||||
|
x4 |
|
x5 |
|
|
|
|
|
|
|
|
|
|
u7 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Рис. 1.28
1.14.9. Построить π -схемы для формул:
а) f (x, y, z)= xyz Ù (xz Ú yz)Ú x yz Ú x y ;
б) f (x1, x2 )= (x1 Ú x2 )Ù x3 Ú x1x2 Ú x2 ; в) f (x, y, z)= (x ® z)(y ® z)® (x ® y).
1.14.10. Найти функции, реализуемые контактными схемами, изображёнными на рис. 1.29.
а) |
x |
x |
x |
x |
б) |
а |
x2 |
|
xn-2 |
|
xn-1 |
|
|
x |
|
… |
|
|
x2 |
x4 |
... |
x |
x |
|
x1 |
|
|
|
|
|
|
|||||||
а |
|
|
|
|
b |
|
|
n-1 |
n |
|
||
y1 |
y2 |
yn-1 |
yn |
|
|
|
|
|
|
|
||
|
|
|
x2 |
|
xn-2 |
|
xn-1 |
b |
||||
|
|
x2 |
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
||||
в) |
x1 |
|
|
|
|
|
|
|
|
|
|
|
|
а |
x2 |
b |
|
|
|
|
|
|
|
|
|
|
|
|
x3 |
|
|
|
|
|
|
|
|
|
|
|
x2 |
|
|
|
|
|
|
|
|
|
|
1.14.11. Варианты расчётно-графической работы. Задание к расчётно-графической работе.
1.По таблице истинности найти СДНФ формулы алгебры логики.
2.Доказать равенство.
3. По данной матрице смежности вершин P или инциденций R построить граф и найти его метрические характеристики (эксцентриситеты вершин, радиус и диаметр графа).
4.Восстановить булеву функцию по данной релейно-контактной схеме ( см. рис. 1.30-1.44) или построить релейно-контактную схему по данной функции.
Вариант 1
1.f (x, y)= (x Ù y)® x Ù (x Ù y)® y ;
2.A Ç (B ÈC)= (A Ç B)È (AÇ C);
|
æ0 |
1 |
1 |
1 |
|
0 |
ö |
|
|
|
|
ç |
1 |
0 |
1 |
1 |
|
0 |
÷ |
|
|
|
ç |
|
÷ |
|
|
|||||
3. P = ç |
1 1 0 |
1 |
1 |
÷ |
; |
|
||||
|
ç |
|
1 |
1 |
0 |
|
1 |
÷ |
|
|
|
ç1 |
|
÷ |
|
|
|||||
|
ç |
0 |
0 |
1 |
1 |
|
0 |
÷ |
|
|
|
è |
|
ø |
|
|
|||||
|
|
|
x |
y |
z |
x |
x |
|
y |
|
4. |
|
|
|
|
|
|
t |
|||
|
|
|
|
|
|
|
|
|||
a |
|
|
t |
y |
|
|
|
z b |
||
|
|
z |
|
x |
|
|||||
|
|
|
|
Рис. 1.30 |
|
|
|
|
||
Вариант 2
1.f (x, y, z)= (x Ù (y Ú z))® (x Ù y)Ú z ;
2.(A \ B)\ C = (A \ C)\ (B \ C);
49

æ |
1 |
1 |
1 |
0 |
0 |
0 |
0 |
ö |
|
ç |
0 |
0 |
-1 |
1 |
1 |
0 |
0 |
÷ |
|
ç |
÷ |
|
|||||||
3. R = ç |
-1 0 |
0 |
0 |
0 |
1 |
1 |
÷ |
; |
|
ç |
0 |
-1 |
0 |
0 |
-1 0 |
|
÷ |
|
|
ç |
-1÷ |
|
|||||||
ç |
0 |
0 |
0 |
-1 0 |
-1 0 |
÷ |
|
||
è |
ø |
|
|||||||
4.f (x, y, z)= x(yz Ú yz)Ú x(yz Ú yz).
Вариант 3
1.f (x, y, z)= (x ® y)Ù ((y ® z)® x);
2.A \ (A \ B)= AÇ B ;
|
æ0 |
|
1 |
1 |
1 |
0 |
ö |
|
|
|
ç |
0 |
|
0 |
0 |
1 |
1 |
÷ |
|
|
ç |
|
÷ |
|
|||||
3. P = ç |
0 |
0 0 0 0 |
÷ |
; |
|||||
|
ç |
|
|
0 |
0 |
0 |
1 |
÷ |
|
|
ç0 |
|
÷ |
|
|||||
|
ç |
0 |
|
0 |
1 |
0 |
0 |
÷ |
|
|
è |
|
ø |
|
|||||
|
x |
|
|
|
z |
t |
|
|
|
|
y |
|
z |
x |
|
||||
4. |
a |
|
|
|
b |
||||
|
|
x |
y |
|
t |
|
|||
|
|
|
|
|
|
|
|
||
y
x
Рис. 1.31
Вариант 4
1.f (x, y, z)= x Ù y Ú y Ù z Ú x Ù z ;
2.A Ç (B \ C)= (A Ç B)\ C ;
æ1 |
1 |
1 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
0ö |
|
||
ç |
1 |
0 |
0 |
0 |
1 |
1 |
0 |
0 |
0 |
0 |
0 |
÷ |
|
ç |
÷ |
|
|||||||||||
ç |
0 |
1 |
0 |
0 |
0 |
0 |
1 |
1 |
1 |
0 |
0 |
÷ |
; |
3. R = ç |
|
0 |
0 |
1 |
0 |
1 |
1 |
0 |
0 |
1 |
|
÷ |
|
ç0 |
0÷ |
|
|||||||||||
ç |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
0 |
1 |
1 |
÷ |
|
ç |
÷ |
|
|||||||||||
ç |
0 |
0 |
1 |
0 |
1 |
0 |
0 |
0 |
1 |
0 |
1 |
÷ |
|
è |
ø |
|
|||||||||||
4.f (x, y, z)= ((x ® y)® (z ® x))® (y ® z).
Вариант 5
1.f (x, y, z)= (x Ù (y Ú x))Ù ((y ® x)Ú y);
2.(A Ç B)È (A Ç B)= A ;
æ |
0 |
1 |
1 |
1 |
1 |
ö |
|
ç |
1 |
0 |
1 |
1 |
1 |
÷ |
|
ç |
÷ |
|
|||||
3. P = ç |
1 |
1 |
0 |
1 |
1 |
÷ |
; |
ç |
1 |
1 |
1 |
0 |
1 |
÷ |
|
ç |
÷ |
|
|||||
ç |
1 |
1 |
1 |
1 |
0 |
÷ |
|
è |
ø |
|
50

|
|
x x |
4. |
a |
x |
x |
x
y |
z |
u |
|
|
|
y |
z |
u |
t |
t |
|
y |
z |
u |
|
||
t |
b |
||||
y |
z |
u |
t |
||
t |
|||||
y |
z |
u |
|
||
Рис. 1.32 |
|
|
|
||
Вариант 6
1.f (x, y, z)= x Ù y Ú x Ù z Ú x Ù y Ù z ;
2.A \ (B ÇC)= (A \ B)È (A \ C);
|
æ |
1 |
1 |
|
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 ö |
|
|||
|
ç |
0 |
-1 |
1 |
1 |
1 |
0 |
0 |
0 |
0 |
0 |
÷ |
|
|||
|
ç |
÷ |
|
|||||||||||||
3. |
ç |
0 |
0 |
|
0 |
0 |
-1 1 1 1 0 0 |
÷ |
; |
|||||||
R = ç |
0 |
0 |
|
-1 0 |
0 -1 0 |
0 |
1 |
|
÷ |
|||||||
|
ç |
|
0 ÷ |
|
||||||||||||
|
ç |
-1 0 0 -1 |
0 |
0 |
-1 0 |
0 |
1 |
÷ |
|
|||||||
|
ç |
÷ |
|
|||||||||||||
|
ç |
0 |
0 |
|
0 |
0 |
0 |
0 |
0 |
|
|
|
÷ |
|
||
|
è |
|
-1 -1 -1ø |
|
||||||||||||
4. |
f (x, y, z)= x |
|
Ú z Ú ( |
|
|
|
. |
|
|
|
|
|
|
|||
y |
x |
Ú y)z |
|
|
|
|
|
|
||||||||
Вариант 7
1.f (x, y, z)= x Ù y Ù z Ú x Ù y Ù z Ú x Ù y Ù z ;
2.A \ B = A \ (A Ç B);
|
æ0 |
0 |
1 |
1 |
0 |
0 |
ö |
|
|
|
ç |
1 |
0 |
1 |
1 |
1 |
0 |
÷ |
|
|
ç |
÷ |
|
||||||
3. |
ç |
0 |
0 |
0 |
1 |
1 |
1 |
÷ |
; |
P = ç |
|
0 |
0 |
0 |
1 |
1 |
÷ |
||
|
ç0 |
÷ |
|
||||||
|
ç |
0 |
0 |
0 |
0 |
0 |
1 |
÷ |
|
|
ç |
÷ |
|
||||||
|
ç |
0 |
0 |
0 |
0 |
0 |
0 |
÷ |
|
|
è |
ø |
|
||||||
|
|
|
x |
|
|
y |
|
|
|
4. |
a |
|
|
|
u |
|
|
|
|
|
z |
|
|
t |
b |
|
|
||
|
|
|
|
|
|
|
|
||
|
|
|
Рис. 1.33 |
|
|
|
|
||
Вариант 8
1.f (x, y, z)= x Ù y Ù z Ú x Ù y Ù z Ú x Ù y Ù z ;
2.(AÈ B)Ç A = A Ç B ;
|
æ |
1 |
1 |
1 |
1 |
0 |
0 |
0 |
0 |
0 |
0ö |
|
|||||
|
ç |
0 |
0 |
1 |
0 |
1 |
1 |
1 |
0 |
0 |
0 |
÷ |
|
||||
|
ç |
÷ |
|
||||||||||||||
3. |
R = ç |
0 |
0 |
0 |
1 |
0 |
0 |
1 |
1 |
1 |
0 |
÷ |
; |
||||
|
ç |
0 |
1 |
0 |
0 |
1 |
0 |
0 |
1 |
0 |
|
÷ |
|
||||
|
ç |
1÷ |
|
||||||||||||||
|
ç |
1 |
0 |
0 |
0 |
0 |
1 |
0 |
0 |
1 |
1 |
÷ |
|
||||
|
è |
ø |
|
||||||||||||||
4. |
f (x, y, z)= ( |
|
Ú |
|
)Ù ((x Ú y)Ù |
|
Ú |
|
)Ú x Ù y Ù z . |
||||||||
x |
y |
z |
z |
||||||||||||||
51

Вариант 9
1.f (x, y, z)= (x Ù (y Ú z))® (x Ù y)Ú z ;
2.(A È B) = A Ç B ;
|
æ |
0 |
1 |
1 |
1 |
0 |
ö |
|
|
ç |
1 |
0 |
1 |
1 |
1 |
÷ |
|
|
ç |
÷ |
|
|||||
3. P = ç |
1 |
1 |
0 |
1 |
1 |
÷ |
; |
|
|
ç |
1 |
1 |
1 |
0 |
1 |
÷ |
|
|
ç |
÷ |
|
|||||
|
ç |
0 |
1 |
1 |
1 |
0 |
÷ |
|
|
è |
ø |
|
|||||
|
|
|
x |
|
|
|
|
|
|
x |
|
|
y |
z |
|
|
|
|
|
|
|
|
|
|
||
4. |
a |
y |
|
|
z |
b |
|
|
|
|
|
|
|||||
x |
|
|
z |
|
||||
y
Рис. 1.34
Вариант 10
1.f (x, y, z)= (x ® (y ® z))® ((x ® y)® (x ® z));
2.A \ (B ÈC)= (A \ B)Ç (A \ C);
æ |
1 |
-1 0 0 |
0 0 1 0 0 ö |
|
|||||||
ç |
-1 |
1 |
1 |
-1 |
0 |
1 |
0 |
0 |
0 |
÷ |
|
ç |
÷ |
|
|||||||||
ç |
0 |
0 |
-1 |
1 |
1 |
0 |
0 |
0 |
0 |
÷ |
; |
3. R = ç |
0 |
0 |
0 |
0 |
0 |
0 |
-1 1 |
|
÷ |
||
ç |
0 ÷ |
|
|||||||||
ç |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
-1 1 |
÷ |
|
|
ç |
÷ |
|
|||||||||
ç |
0 |
0 |
0 |
0 |
-1 -1 0 |
0 |
|
÷ |
|
||
è |
-1ø |
|
|||||||||
4.f (x, y, z)= (x Ú y Ú z)Ù (x Ú y).
Вариант 11
1.f (x, y, z)= (x ® y)® ((x ® (y ® z))® (x ® z));
2.(A Ç B)È (C Ç D)= (A ÈC)Ç (B ÈC)Ç (AÈ D)Ç (B È D);
|
æ |
0 |
1 |
0 |
1 |
1 |
ö |
|
|
ç |
1 |
0 |
1 |
1 |
0 |
÷ |
|
|
ç |
÷ |
|
|||||
3. P = ç |
0 |
1 |
0 |
1 |
1 |
÷ |
; |
|
|
ç |
0 |
0 |
1 |
0 |
1 |
÷ |
|
|
ç |
÷ |
|
|||||
|
ç |
0 |
0 |
0 |
1 |
0 |
÷ |
|
|
è |
ø |
|
|||||
|
|
x |
y |
|
z |
|
|
|
4. |
|
|
|
|
|
|
||
|
|
|
|
|
|
|
||
a |
x |
y |
|
z |
z |
b |
||
|
|
|
|
|||||
y
Рис. 1.35
Вариант 12
1.f (x, y, z)= (x Ú y)Ù z Ú x Ù y Ù z ;
2.A Ç B Í B Í A È B ;
52

æ |
1 |
1 |
1 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0ö |
|
ç |
0 |
0 |
0 |
1 |
1 |
1 |
1 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
÷ |
ç |
÷ |
||||||||||||||||
ç |
0 |
0 |
1 |
0 |
0 |
0 |
1 |
0 |
1 |
1 |
1 |
0 |
0 |
0 |
0 |
0 |
÷ |
ç |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
0 |
0 |
1 |
1 |
1 |
0 |
0 |
|
÷ |
3. R = ç |
0÷ ; |
||||||||||||||||
ç |
1 |
0 |
0 |
0 |
1 |
1 |
0 |
0 |
1 |
0 |
0 |
1 |
0 |
1 |
1 |
0 |
÷ |
ç |
÷ |
||||||||||||||||
ç |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
1 |
0 |
1 |
÷ |
ç |
÷ |
||||||||||||||||
è |
0 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
0 |
1 |
1 |
ø |
4.f (x, y, z)= x Ù (y Ú z)Ú y Ù (x Ú z).
Вариант 13
1.f (x, y, z)= x Ù z Ú z Ù (y Ú z)Ú (x Ú y)Ù z ;
2.A Å B = B Å A ;
æ |
0 |
1 |
0 |
0 |
1 |
0 |
1 |
ö |
ç |
1 |
0 |
1 |
1 |
1 |
0 |
1 |
÷ |
ç |
÷ |
|||||||
ç |
0 |
1 |
0 |
1 |
1 |
1 |
0 |
÷ |
ç |
0 |
1 |
1 |
0 |
1 |
0 |
|
÷ |
3. P = ç |
0÷ ; |
|||||||
ç |
1 |
1 |
1 |
1 |
0 |
1 |
0 |
÷ |
ç |
÷ |
|||||||
ç |
0 |
0 |
1 |
0 |
1 |
0 |
1 |
÷ |
ç |
÷ |
|||||||
è |
1 |
1 |
0 |
0 |
0 |
1 |
0 |
ø |
|
x |
x |
x |
4. |
y |
y |
y |
a |
z |
b |
|
|
z |
z |
|
|
|
Рис. 1.36 |
|
Вариант 14
1.f (x, y, z)= (x Ù y)« (x Ù z);
2.(A Ç B)´ C = (A ´ C)Ç (B ´ C);
|
æ |
1 |
1 |
-1 0 |
0 |
-1 0 |
0 ö |
|
|||
|
ç |
0 |
-1 |
1 |
1 |
1 |
0 |
-1 0 |
÷ |
|
|
3. |
ç |
÷ |
; |
||||||||
R = ç |
-1 |
0 |
0 |
0 |
-1 0 |
0 |
|
÷ |
|||
|
ç |
-1 |
|
||||||||
|
|
|
|
|
|
|
|
|
÷ |
|
|
|
ç |
0 |
0 |
0 |
-1 0 |
1 |
1 |
1 |
÷ |
|
|
|
è |
ø |
|
||||||||
4.f (x, y, z,t)= x Ù y Ù (z Ù t Ú y Ú x)Ú x Ù (z Ú t)Ù (x Ú y).
Вариант 15
1.f (x, y, z)= x Ù (y Ú z « xy);
2.(A´ B)È (C ´ D)Í (A È C)´(B È D);
53

|
æ0 |
1 |
0 |
1 |
0 |
1 |
0 |
ö |
|
|
ç |
0 |
0 |
1 |
1 |
0 |
1 |
0 |
÷ |
|
ç |
÷ |
|||||||
|
ç |
1 |
0 |
0 |
0 |
1 |
0 |
1 |
÷ |
|
ç |
|
|
|
|
|
|
|
÷ |
3. P = ç0 0 0 0 1 1 1÷ ; |
|||||||||
|
ç |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
÷ |
|
ç |
÷ |
|||||||
|
ç |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
÷ |
|
ç |
÷ |
|||||||
|
è |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
ø |
4. |
x |
z |
|
x |
y |
z |
x |
|
|
|
|
|
|
|
|
|
|||
a |
|
y |
|
x |
|
z |
z |
b |
|
|
y |
|
y |
|
|||||
|
|
|
|
|
|||||
|
|
|
|
Рис. 1.37 |
|
|
|
||
Вариант 16
1.f (x, y, z)= (x Ù y)Ú (z « x Ú y);
2.(A Ç B)´(C Ç D)= (A´C)Ç (B ´ D);
æ1 |
1 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0ö |
|
||
ç |
0 |
0 |
1 |
1 |
1 |
1 |
0 |
0 |
0 |
0 |
0 |
÷ |
|
ç |
÷ |
|
|||||||||||
ç |
0 |
0 |
0 |
0 |
0 |
1 |
1 |
1 |
1 |
0 |
0 |
÷ |
; |
3. R = ç |
|
0 |
0 |
1 |
0 |
0 |
1 |
0 |
0 |
1 |
|
÷ |
|
ç1 |
0÷ |
|
|||||||||||
ç |
0 |
0 |
0 |
0 |
1 |
0 |
0 |
1 |
0 |
1 |
1 |
÷ |
|
ç |
÷ |
|
|||||||||||
ç |
0 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
0 |
1 |
÷ |
|
è |
ø |
|
|||||||||||
4.f (x, y, z,t)= x Ú y Ù z Ù t Ú y Ù z Ù t Ú y Ú y Ù z Ù t .
Вариант 17
1.f (x, y, z)= (x « y)® (z Ú xy);
2.A Ç (B Å C)= (A Ç B)Å (A Ç C);
|
æ0 |
1 |
0 |
0 |
0 |
1 |
ö |
|
|
|
|
ç |
1 |
0 |
1 |
1 |
0 |
1 |
÷ |
|
|
|
ç |
÷ |
|
|
||||||
3. |
ç |
0 |
1 |
0 |
1 |
0 |
0 |
÷ |
; |
|
P = ç |
|
1 |
1 |
0 |
1 |
1 |
÷ |
|
||
|
ç0 |
÷ |
|
|
||||||
|
ç |
0 |
0 |
0 |
1 |
0 |
1 |
÷ |
|
|
|
ç |
÷ |
|
|
||||||
|
ç |
1 |
1 |
0 |
1 |
1 |
0 |
÷ |
|
|
|
è |
ø |
|
|
||||||
|
y |
|
|
|
|
x |
|
|
|
|
|
z |
x |
|
|
|
|
|
|
|
|
4. |
a |
|
|
|
x |
|
|
y |
b |
|
|
|
|
|
|
|
|||||
y |
|
|
|
|
|
|
|
|
||
|
z |
|
y |
|
z |
|
|
|
||
|
|
|
|
|
|
|
|
|||
|
|
|
|
Рис. 1.38 |
|
|
|
|
||
Вариант 18
1.f (x, y, z)= x ® (y ® (z « xy));
2.A È B = A Å B Å (A Ç B);
54
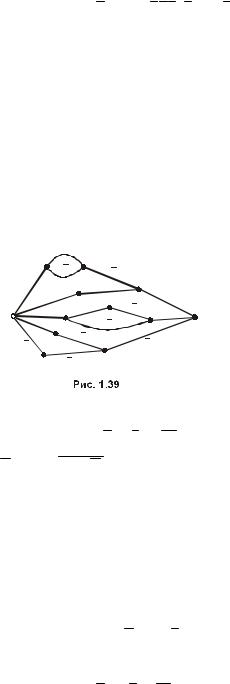
æ 1 |
1 |
|
1 |
0 |
0 |
0 |
|
-1 |
0 |
0 |
0 |
|||
ç |
0 |
0 |
|
-1 |
1 |
1 |
1 |
|
1 |
|
0 |
0 |
0 |
|
ç |
|
|
|
|||||||||||
3. R = ç |
0 |
-1 |
0 |
|
0 |
0 |
-1 |
0 |
|
1 |
-1 0 |
|||
ç |
|
0 |
|
0 |
|
-1 0 |
0 |
|
0 |
|
0 |
1 |
1 |
|
ç 0 |
|
|
|
|
||||||||||
ç |
-1 0 |
0 |
0 |
-1 0 |
0 |
-1 0 |
-1 |
|||||||
è |
||||||||||||||
4.f (x, y, z)= (x Ú y)(xyz Ú x yz)(x Ú z)(z Ú y).
Вариант 19
1.f (x, y, z)= (x ® y)« (x ® z);
2.A ´ (B \ C) = (A ´ B)\ (A´ C);
æ0 |
0 |
0 |
1 |
0 |
0 |
ö |
|
|
ç |
0 |
0 |
0 |
0 |
1 |
0 |
÷ |
|
ç |
÷ |
|
||||||
ç |
1 |
0 |
0 |
0 |
1 |
0 |
÷ |
; |
3. P = ç |
|
1 |
0 |
0 |
0 |
0 |
÷ |
|
ç0 |
÷ |
|
||||||
ç |
0 |
1 |
0 |
0 |
0 |
0 |
÷ |
|
ç |
÷ |
|
||||||
ç |
0 |
0 |
1 |
1 |
1 |
0 |
÷ |
|
è |
ø |
|
||||||
|
|
|
x |
|
|
|
|
|
|
|
|
y |
x |
|
|
|
|
y |
z |
|
y |
|
|
|
x |
|
4. |
|
x |
|
z |
|
|
||
|
z |
|
|
|
y |
|||
a |
|
y |
z |
x |
|
|
|
b |
z |
|
|
|
|
y |
|
|
|
|
|
|
|
|
|
|
||
x
-1ö
÷
0 ÷
0 ÷÷ ;
0 ÷
1 ÷ø
Вариант 20
1.f (x, y, z)= x ® (y Ú (z ® xy));
2.(AÈ B)= (A Ç B);
æ1 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
ö |
|
|
ç |
0 |
1 |
1 |
1 |
0 |
0 |
0 |
0 |
÷ |
|
ç |
÷ |
|
||||||||
ç |
0 |
0 |
0 |
1 |
1 |
1 |
0 |
0 |
÷ |
; |
3. R = ç |
|
0 |
0 |
0 |
1 |
0 |
1 |
0 |
÷ |
|
ç1 |
÷ |
|
||||||||
ç |
0 |
0 |
1 |
0 |
0 |
0 |
1 |
1 |
÷ |
|
ç |
÷ |
|
||||||||
ç |
0 |
0 |
0 |
0 |
0 |
1 |
0 |
1 |
÷ |
|
è |
ø |
|
||||||||
4.f (x, y, z,t)= xyz Ú x yz Ú xyzt .
Вариант 21
1.f (x, y, z)= (x Ù y « z)Ú xy ;
2.(A \ B)\ C = A \ (B È C);
æ |
0 |
0 |
1 |
1 |
0 |
ö |
|
ç |
0 |
0 |
0 |
1 |
1 |
÷ |
|
ç |
÷ |
|
|||||
3. P = ç |
1 |
0 |
0 |
0 |
1 |
÷ |
; |
ç |
1 |
1 |
0 |
0 |
1 |
÷ |
|
ç |
÷ |
|
|||||
ç |
0 |
1 |
1 |
1 |
0 |
÷ |
|
è |
ø |
|
55

|
|
|
x |
|
4. |
|
y |
y |
|
a |
z |
x |
b |
z
y
Рис. 1.40
Вариант 22 1. f (x, y, z)= (x ® y)Ù (y ® z)Ù (z ® x);
2. |
|
A |
È |
B |
= A Ç B ; |
|
|
|
|
|
|
|
|
||||
|
æ 1 |
1 |
|
0 |
0 |
0 |
0 |
|
|
0 |
|||||||
|
ç |
0 |
-1 |
-1 |
1 |
0 |
0 |
|
|
0 |
|||||||
|
ç |
|
|
||||||||||||||
3. |
ç |
0 |
0 |
|
0 |
-1 |
-1 |
1 |
|
|
0 |
||||||
|
R = ç |
-1 |
0 |
|
0 |
0 |
1 |
0 |
|
|
-1 |
||||||
|
ç |
|
|
|
|||||||||||||
|
ç |
0 |
0 |
|
1 |
0 |
0 |
0 |
|
|
1 |
||||||
|
ç |
|
|
|
|||||||||||||
|
ç |
0 |
0 |
|
0 |
0 |
0 |
-1 |
|
0 |
|||||||
|
è |
|
|
||||||||||||||
4. |
f (x, y, z)= (y |
|
® (x |
|
|
|
|
|
|
|
|||||||
z |
yz Ú xyz))® x . |
|
|||||||||||||||
0 ö
÷
0 ÷
0 ÷÷ ;
0 ÷
1 ÷÷ -1÷ø
Вариант 23
1.f (x, y, z)= (x Ú y)Ù z Ú x Ù y Ú y ;
2.A \ B = A Å (A Ç B);
|
æ0 |
0 |
0 |
1 |
0 |
ö |
|
|
|
ç |
0 |
0 |
0 |
0 |
0 |
÷ |
|
|
ç |
÷ |
|
|||||
3. P = ç |
1 0 0 0 0 |
÷ |
; |
|||||
|
ç |
|
1 |
0 |
0 |
1 |
÷ |
|
|
ç0 |
÷ |
|
|||||
|
ç |
0 |
1 |
1 |
0 |
0 |
÷ |
|
|
è |
ø |
|
|||||
|
|
|
|
|
|
|
x |
|
|
|
|
x |
x |
|
|
y |
|
4. |
a |
|
z |
y |
|
|
z |
b |
|
|
|
|
|||||
t |
t |
|
|
Рис. 1.41 |
|
Вариант 24
1.f (x, y, z)= (x ® (y ® z))® ((x ® y)® (x ® z));
2.A È B = (A Å B)È (A Ç B);
|
æ1 |
1 |
1 |
0 |
0 |
0 |
0 |
0 |
0ö |
|
|||||
|
ç |
0 |
0 |
0 |
1 |
1 |
1 |
0 |
0 |
0 |
÷ |
|
|||
|
ç |
÷ |
|
||||||||||||
3. |
ç |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
1 |
1 |
÷ |
; |
|||
R = ç |
|
0 |
1 |
0 |
0 |
1 |
0 |
0 |
|
÷ |
|||||
|
ç0 |
1÷ |
|
||||||||||||
|
ç |
0 |
1 |
0 |
0 |
1 |
0 |
0 |
1 |
0 |
÷ |
|
|||
|
ç |
÷ |
|
||||||||||||
|
ç |
1 |
0 |
0 |
1 |
0 |
0 |
1 |
0 |
0 |
÷ |
|
|||
|
è |
ø |
|
||||||||||||
4. |
f (x, y, z)= |
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
||||
xyz Ú xyzz . |
|
|
|
|
|
||||||||||
Вариант 25
1.f (x, y, z)= (y ® x Ù z)Ù (x Ú z ® y);
56

2. A È (B ÇC)= (A È B)Ç (AÈ C);
|
æ0 |
1 |
1 |
1 |
0 |
0 |
ö |
|
|
|
ç |
1 |
0 |
0 |
1 |
1 |
1 |
÷ |
|
|
ç |
÷ |
|
||||||
|
ç |
1 |
0 |
0 |
1 |
1 |
1 |
÷ |
; |
3. P = ç |
|
1 |
1 |
0 |
0 |
0 |
÷ |
||
|
ç1 |
÷ |
|
||||||
|
ç |
0 |
1 |
1 |
0 |
0 |
0 |
÷ |
|
|
ç |
÷ |
|
||||||
|
ç |
0 |
1 |
1 |
0 |
0 |
0 |
÷ |
|
|
è |
ø |
|
||||||
|
|
x |
y |
|
z |
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
z |
b |
|
|
|
|
4. |
a |
|
x |
|
|
|
|
||
|
|
y |
|
|
|
||||
|
|
z |
|
z |
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
Рис. 1.42 |
|
|
|
|
||
Вариант 26
1.f (x, y, z)= (x Ú y Ú z)® ((x Ú y)Ù (x Ú z));
2.AÅ (A Å B)= B ;
|
æ 1 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
|
0 |
|
|
ç |
-1 |
1 |
1 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
|
0 |
|
ç |
|
|||||||||||
|
ç |
0 |
0 |
0 |
-1 |
1 |
1 |
-1 0 |
0 |
0 |
|
0 |
|
|
ç |
|
|
|
|
|
|
|
|
|
0 |
0 |
|
3. |
ç 0 0 0 0 0 0 0 -1 0 |
||||||||||||
R = ç |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
1 |
-1 0 |
|
0 |
||
|
ç |
|
|||||||||||
|
ç |
0 |
0 |
-1 |
0 |
0 |
-1 |
0 |
0 |
1 |
-1 |
0 |
|
|
ç |
||||||||||||
|
ç |
0 |
-1 |
0 |
0 |
-1 |
0 |
0 |
0 |
0 |
1 |
|
1 |
|
ç |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
|
-1 |
|
è |
|
|||||||||||
4.f (x, y, z)= x yz Ú xyz Ú xyz Ú x yz .
Вариант 27
1.f (x1, x2 ,...,xn )= x1 ® (x2 ® (... ® (xn−1 ® xn )...));
2.A´(B \ C)= (A´ B)\ (A´C);
|
æ1 |
1 |
1 |
0 |
ö |
|
|
|
ç |
0 |
0 |
0 |
1 |
÷ |
|
3. |
ç |
÷ |
; |
||||
P = ç |
0 |
0 |
0 |
1 |
÷ |
||
|
ç |
÷ |
|
||||
|
ç |
1 |
0 |
0 |
0 |
÷ |
|
|
è |
ø |
|
||||
|
|
|
x |
y |
|
z |
|
|
|
|
|
|
|
||
|
|
|
|
|
|
b |
|
4. |
|
|
|
x |
|
|
|
a |
|
|
z |
|
y |
|
|
z
y
Рис. 1.43
0 ö
÷
0 ÷
-1÷÷
0 ÷
0 ÷÷ ;
0 ÷
÷
0 ÷
1 ÷ø
Вариант 28
1.f (x, y, z)= (x Ú y ® x Ù z)® (x ® x)Ú y Ù z ;
2.A ´ (B Ç C) = (A ´ B)Ç (A ´ C);
57

|
æ1 |
1 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
|
|
ç |
0 |
0 |
1 |
1 |
1 |
1 |
1 |
0 |
0 |
0 |
0 |
|
ç |
|||||||||||
|
ç |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
1 |
1 |
1 |
0 |
|
ç |
|
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
0 |
3. |
ç0 |
|||||||||||
R = ç |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
|
|
ç |
|||||||||||
|
ç |
0 |
0 |
0 |
0 |
0 |
1 |
0 |
0 |
1 |
0 |
1 |
|
ç |
|||||||||||
|
ç |
0 |
1 |
0 |
0 |
1 |
0 |
0 |
1 |
0 |
0 |
0 |
|
ç |
1 |
0 |
0 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
|
è |
|||||||||||
4.f (x, y, z,t)= xt(x Ú zy Ú t)Ú xz Ú xyz .
Вариант 29
1.f (x, y, z)= xyz Ú ((x Ú y)« (x Ù z));
2. |
если A B , то A C B C ; |
|
|||||||||
|
æ0 |
1 |
0 |
0 |
1 |
0 |
0 |
0 |
ö |
|
|
|
ç |
1 |
0 |
1 |
0 |
0 |
1 |
1 |
0 |
÷ |
|
|
ç |
÷ |
|
||||||||
|
ç |
0 |
1 |
0 |
1 |
0 |
1 |
1 |
0 |
÷ |
|
|
ç |
|
0 |
1 |
0 |
0 |
0 |
0 |
1 |
÷ |
|
3. |
ç0 |
÷ |
; |
||||||||
P = ç |
1 |
0 |
0 |
0 |
0 |
1 |
0 |
0 |
÷ |
||
|
ç |
÷ |
|
||||||||
|
ç |
0 |
1 |
1 |
0 |
1 |
0 |
1 |
0 |
÷ |
|
|
ç |
÷ |
|
||||||||
|
ç |
0 |
1 |
1 |
0 |
0 |
1 |
0 |
1 |
÷ |
|
|
ç |
0 |
0 |
0 |
1 |
0 |
0 |
1 |
0 |
÷ |
|
|
è |
ø |
|
||||||||
0 |
0ö |
|
0 |
0 |
÷ |
÷ |
||
0 |
0 |
÷ |
|
|
÷ |
00 ;
00
10÷÷÷÷
÷
1 1÷
0 1÷ø
|
x |
y |
4. |
z |
y |
a |
b |
|
|
x |
z |
|
|
y |
|
Рис. 1.44 |
|
Вариант 30
1.f (x, y, z)= ((x ® y)® (z ® x))® (y ® z);
2. |
если A B и C D , то A×C B × D ; |
|||||||||||
|
æ |
1 |
1 |
0 |
0 |
|
-1 -1 0 ö |
|
||||
|
ç |
0 |
-1 |
1 |
1 |
|
1 |
0 |
0 |
÷ |
|
|
3. |
ç |
|
÷ |
; |
||||||||
R = ç |
|
|
|
|
|
|
|
|
|
÷ |
||
|
ç |
-1 |
0 |
0 |
-1 |
0 |
1 |
-1÷ |
|
|||
|
ç |
0 |
0 |
-1 |
0 |
|
0 |
0 |
1 |
÷ |
|
|
|
è |
|
ø |
|
||||||||
4. |
f (x, y, z,t)= x(y Ú zt) |
|
Ú (x Ú t)yz . |
|
|
|
||||||
z |
|
|
|
|||||||||
58
