4.7. Турбулентное течение в каналах постоянного сечения

Структура при турбулентном движении жидкости иная, чем при ламинарном (рис. 4.8). Если рассматривать поперечное сечение потока в трубе, то у стенки трубы мы имеем пограничный слой, а за пограничным слоем – турбулентное ядро течения. Пограничный слой состоит из ламинарного подслоя , в котором течение жидкости происходит в ламинарном режиме, и переходного, в котором происходит переход из ламинарного режима течения в турбулентный. Пограничный слой имеет толщину от 0,1 мм до нескольких миллиметров. При увеличении скорости потока толщина ламинарного подслоя уменьшается, так как оказывается, что число Рейнольдса для ламинарного подслоя есть величина постоянная  –.

На распределение скоростей по живому сечению при турбулентном режиме течения влияет шероховатость стенок, ограждающих поток. Шероховатость является одной из причин появления вихрей у стенок и дополнительных гидравлических сопротивлений, а, следовательно, и потерь энергии при движении потока. Для оценки выступов шероховатости в гидравлике введено понятие абсолютной шероховатости (). Абсолютная шероховатость характеризуется высотой среднего выступа шероховатой поверхности. При этом важен не абсолютный размер бугорков, а отношение() – относительная шероховатость (– относительная гладкость). Одна и та же абсолютная шероховатость может совершенно не оказывать влияние на сопротивление трубы большого диаметра, но способна существенно увеличить сопротивление трубы малого диаметра. Кроме того, на сопротивление влияет характер шероховатости. Простейший случай, – когда бугорки одинакового размера и формы (равномерно-зернистая шероховатость).

Если ламинарный подслой покрывает выступы шероховатости, то труба считается гидравлическигладкой, а если нет,–гидравлическишероховатой. Ввиду того, что геометрические характеристики абсолютной шероховатости не могут в достаточной степени определять сопротивление трубы, введено понятие о гидравлическиэквивалентнойравномерно-зернистой шероховатости Δ_э, которая создает такое же сопротивление, как реальная шероховатость.

При турбулентном движении скорости (мгновенные) отдельных частиц жидкости (макрообъемов) в отдельных точках пространства все время меняются по величине и направлению, т.е. происходит пульсацияскоростей. Однако мгновенные скорости в данной точке пространства колеблются околоосредненнойскорости. Аналогично происходит и пульсация давления по величине.

Установившимсядвижением при турбулентном течении называют такое движение, при котором в любой точке пространства, занятого жидкостью,осредненнаяскорость и гидродинамическое давление не меняются с течением времени.

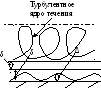
Линии тока

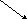
рис. 4.8

В турбулентном потоке, кроме продольного поступательного движения частиц жидкости, существует еще и поперечное, которое приводит к перемешиванию макрообъемов жидкости, в результате чего появляются дополнительные потери энергии и возникают дополнительные касательные напряжения.

Для ламинарного режима касательные напряжения равны

.

При турбулентном движении:

,

где l– путь смещения, он определяется экспериментально для различных параметров течения, зон и геометрии каналов (вблизи стенок труб,K=0,435,x – расстояние от сечения зарождения турбулентного течения до рассматриваемого сечения).

Первый член в последнем выражении характеризует вязкое трение при ламинарном движении, второй – выражает дополнительное касательное напряжение от пульсаций, возникающих при поперечном движении макрообъемов жидкости. С увеличением скорости течения (Re) главное влияние на величину касательных напряжений оказывает второй член и при больших Re касательные напряжения (а, значит, и потери полного напора ) оказываются пропорциональны квадрату градиента скорости.

Обычно под термином вязкие напряжения подразумевают касательные напряжения при ламинарном режиме течения (вязкое трение), а под термином касательные напряжения – напряжения при турбулентном течении (вязкие и дополнительные касательные напряжения).

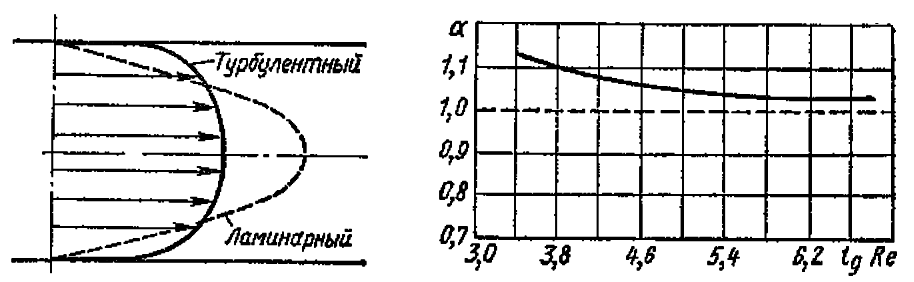
рис. 4.9 Рис. 4.10

1. При ламинарном режиме ,.

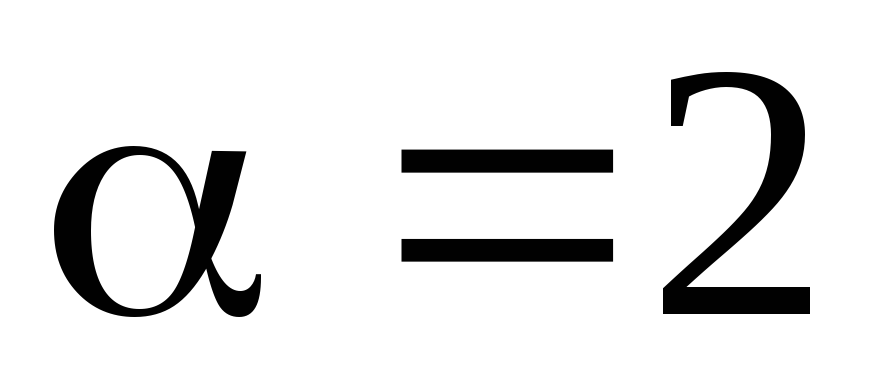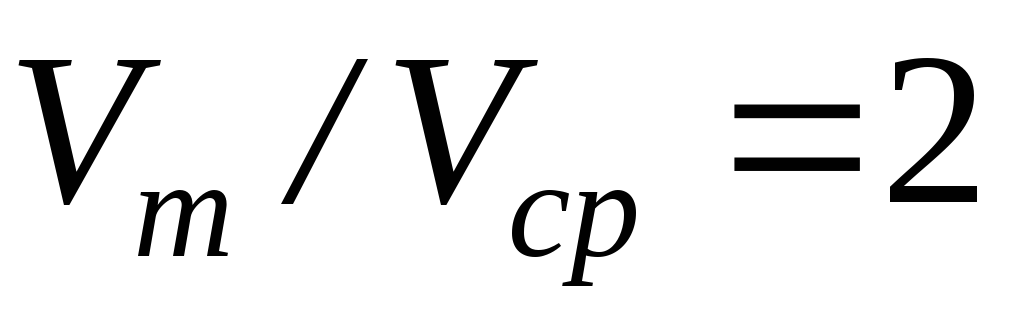2. При турбулентном режиме ,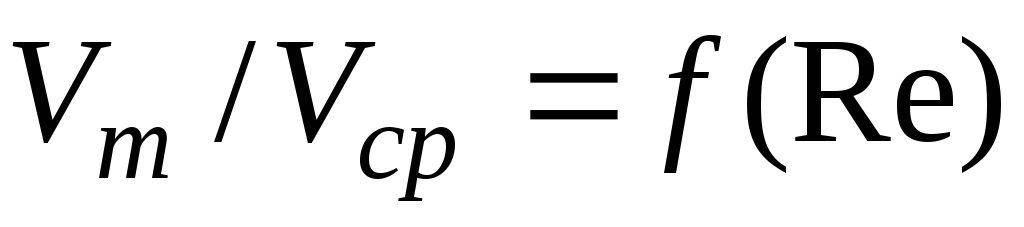– для гидравлически гладких труб;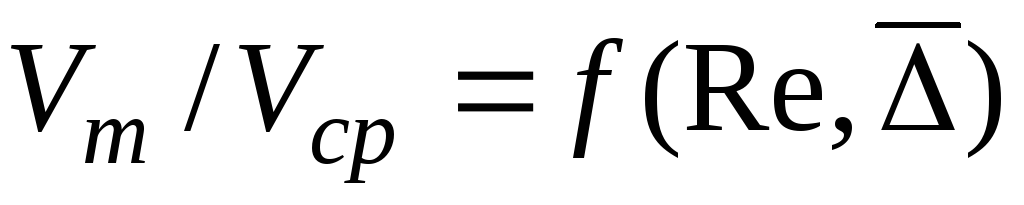– для гидравлически шероховатых.

Для развитого турбулентного режима , т.е. пренебрегаем трением при ламинарном движении.

Характерная зависимость потерь полного напора для различных режимов течения приводятся на рис. 4.10.

При турбулентном режиме течения потери в круглых трубах определяются по формуле Дарси в виде:

,

где λ_т– определяется по зависимостям для турбулентного течения (см. ниже).

В трубах с некруглым сечением в первом приближении – с использованием гидравлического диаметра в виде:

.

Для более точного определения ­потерь – с использованием гидравлического диаметра и поправочного коэффициента , учитывающего форму сечения:

,

где (например, для труб квадратного сечения приRe> 2300 –и); при этом.