Mashkovsky_Lesnaya_biometria

следующим образом:

что и требовалось доказать.

Используя (53) и (18), первое слагаемое в выражении (52) можно преобразовать следующим образом:

Выражение (25) (5 свойство среднего арифметического) можно преобразовать к виду

Далее, используя (54), преобразуем второе слагаемое из выражения (52) следующим образом:

(x1 − x)2 n1 + (x2 − x)2 n2 = n1 + n2

= (x1 )2 n1 −2 x1 x n1 +(x)2 n1 +(x2 )2 n2 −2 x2 x n2 +(x)2 n2 = n1 +n2

= (x1 )2 n1 + (x2 )2 n2 + (x)2 (n1 + n2 ) − 2 x (x1 n1 + x2 n2 ) =

n1 + n2

= (x1 )2 n1 + (x2 )2 n2 + (x)2 (n1 + n2 ) − 2 (x)2 (n1 + n2 ) =

n1 + n2

62

= (x1 )2 n1 + (x2 )2 n2 − (x)2 (n1 + n2 ) .

n1 + n2

Подставляя найденные выражения для слагаемых в выражение (52) и учитывая (53), получим

что и требовалось доказать.

Данное свойство можно обобщить на случай, когда выборка состоит из k групп наблюдений. Чтобы сделать такое обобщение, целесообразно ввести понятия межгрупповой и внутригрупповой дисперсии.

Межгрупповой дисперсией мы будем называть среднюю арифметическую квадратов отклонений групповых средних xi от

средней для всей выборки x (причем в качестве весов при вычислении этой дисперсии используются объемы групп ni ). Эту

дисперсию можно вычислить по формуле

i=1

Внутригрупповой дисперсией, или средней групповых дисперсий,

Si2 мы будем называть среднюю арифметическую групповых дисперсий Si2 . В качестве весов в данном случае используются объемы групп ni :

63

однако в некоторых случаях удобнее иметь показатель, который оценивает разброс данных не в абсолютных величинах, а в относительных. Таким показателем является коэффициент вариации, который показывает, сколько процентов составляет среднеквадратическое отклонение от среднего арифметического:

В биометрии этот показатель часто оказывается весьма полезным. Дело в том, что анализу подвергаются, как правило, объекты живой природы, а они с течением времени изменяют свои размеры: растут. В связи с этим часто необходимо анализировать выборки, сделанные для объектов с разным средним возрастом, а следовательно, и разными средними размерами. Если в таких случаях необходимо сравнить степень изменчивости признака в разных выборках, то удобнее оперировать коэффициентом вариации, так как он дает нам величину вариации по отношению к среднему значению.

Коэффициент асимметрии. Рассмотренные выше показатели довольно полно характеризуют анализируемые признаки, однако ни один из них не отражает степень симметричности распределения наблюдений относительно среднего значения. Ведь на практике довольно часто отклонения признака от среднего арифметического в меньшую и большую стороны носят неодинаковый характер.

Для того чтобы оценить степень такой неравномерности распределения наблюдений относительно среднего арифметического, используют коэффициент асимметрии, который можно вычислить по формуле

n

∑(xi − x)3

или для сгруппированного набора данных:

k

∑ fi (xi − x)3

Коэффициент асимметрии может принимать как положительные, так и отрицательные значения. В том случае, если левая ветвь распределения более пологая и длинная, а вершина кривой смещена вправо относительно среднего арифметического, то

65

коэффициент асимметрии для такого распределения имеет отрицательное значение. Такая асимметрия называется левосторонней, или отрицательной (рис. 8).

Рис. 8. Левосторонняя, или отрицательная, асимметрия кривой распределения

Если распределение имеет более длинную и пологую правую ветвь, а его вершина смещена влево относительно среднего арифметического, то в таком случае имеет место правосторонняя, или положительная, асимметрия (рис. 9). Коэффициент асимметрии в таком случае будет положительным.

Рис. 9. Правосторонняя, или положительная, асимметрия кривой распределения

Эмпирический коэффициент эксцесса. Кроме того, что распределения наблюдений могут отличаться друг от друга по степени асимметричности, они могут иметь разную крутизну: быть островершинными и плосковершинными. В случае островершинной кривой, когда большое число наблюдений группируется в

66

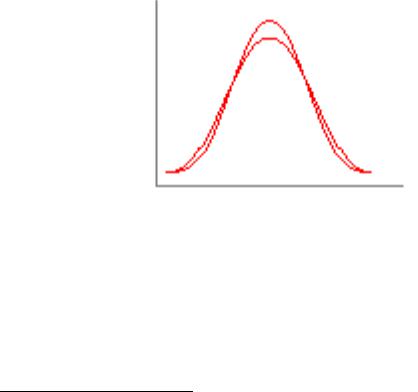
непосредственной близости от центра распределения, говорят о наличии положительного эксцесса. Кривая распределения имеет отрицательный эксцесс, если она является плосковершинной. Для оценки степени крутизны кривой распределения используется коэффициент эксцесса, который вычисляется по формуле

n

∑(xi − x)4

или для сгруппированного набора данных:

k

∑ fi (xi − x)4

Этот коэффициент построен таким образом, что его значение для нормального распределения1, как для наиболее изученного и часто используемого, равен нулю. В том случае, если коэффициент эксцесса принимает положительное значение (положительный эксцесс), распределение вариант будет более крутым, чем нормальное распределение (рис. 10).

Рис. 10. Положительный эксцесс, островершинная кривая

Когда этот показатель меньше нуля (отрицательный эксцесс), наблюдения будут образовывать более плосковершинную кривую, чем нормальное распределение (рис. 11).

1 Нормальное распределение будет рассматриваться в следующей главе.

67

Рис. 11. Отрицательный эксцесс, плосковершинная кривая

Эмпирические моменты. Кроме перечисленных выше показателей, для характеристики эмпирических распределений используется система статистик, называемых моментами. Эмпирический момент порядка q определяется как средняя арифметическая величина из q-тых степеней наблюдаемых значений признака:

n

∑xiq

или в случае сгруппированного набора данных:

k

∑ fi xiq

Такие моменты иногда называют начальными.

Эмпирический начальный момент нулевого порядка всегда равен 1:

Эмпирический начальный момент первого порядка – это не что иное, как средняя арифметическая величина. Действительно, если в формулу (64) подставить значение q =1, то мы получим формулу, выражающую среднее арифметическое значение:

68

задается момент относительно точки c порядка q.

В случае, когда c = 0 , получаем начальные моменты. Моменты относительно средней арифметической ( c = x ) называются центральными:

n

∑(xi − x)q

или для сгруппированного набора данных:

k

∑ fi (xi − x)q

В силу свойства 1 средней арифметической величины, гласящего, что сумма отклонений вариант от средней арифметической величины равна нулю, эмпирический центральный момент первого порядка также равен нулю:

n

∑(xi − x)

Эмпирический центральный момент второго порядка – это не что иное, как выборочная дисперсия:

n

∑(xi − x)2

Эмпирические центральные моменты всех порядков обладают двумя свойствами.

1. Если все наблюдения в анализируемой выборке изменить на постоянную величину c (c [−∞;+∞]) , то центральный момент q-того

порядка не изменится. Действительно, учитывая свойство 2 средней

69

арифметической величины (x + c = x + c) , имеем:

2. Если все наблюдения в анализируемой выборке умножить на константу c (c [−∞;+∞]) , то центральный момент q-того порядка

увеличится в cq раз. Действительно, учитывая свойство 3 средней арифметической (x c = x c) , получим

Если известны моменты q--того порядка и ниже относительно точки a, то на основании этих величин можно определить момент q-того порядка относительно любой другой точки c.

С учетом формулы бинома имеем

Используя выражение (67), получим

70