2.3 Структурная схема проектируемой системы управления

Цель управления: стабилизация давления пара на выходе из парового котла путем изменения расхода природного газа. Структурная схема САУ представлена на рисунке 2.3. На данной схеме приведены входные воздействия и выходные показатели, а также их взаимодействие. Анализ технологического процесса получения пара высокого давления как ОУ позволяет обосновать выбор структуры системы автоматического управления.

Рисунок 2.2 – Структурная схема САУ

Управляющие воздействия вносят с помощью исполнительных устройств, которые изменяют материальные или тепловые потоки. При разработке АСР выбирают один или несколько показателей эффективности процесса, устанавливают необходимые ограничения, находят статические и динамические характеристики объекта регулирования. Анализ статических характеристик позволяет оценить степень влияния одних величин на другие и выявить те регулируемые величины, которые оказывают максимальное воздействие на процесс. Если в объекте имеется несколько независимых величин, их регулируют раздельно, вводя соответствующие контуры регулирования. В объектах с зависимыми регулируемыми величинами используются контуры регулирования, в которых учитывается степень воздействия управляющих сигналов на регулируемые величины.

2.4 Математическая модель процесса

Для вывода передаточной функции по каналу «уровень питательной воды в барабане – расход питательной воды на входе в паровой котел» составим материальный баланс:

где V – объём питательной воды;

, – объёмный расход воздуха и питательной воды.

При увеличении расхода притока воздуха в первый момент времени уровень будет увеличиваться, что приводит к увеличению расхода на выходе, который зависит от уровня. И в некоторый момент ,L= const.

где S_КЛ – проходное сечение клапана;

L – уровень сырья.

Получилось нелинейное уравнение, так как есть , и его необходимо линеаризовать. При небольшом изменении ΔL и S_КЛ уравнение (2.2) можно линеаризовать путём разложения его в ряд Тейлора. Ограничимся первым порядком:

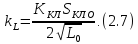
При изменении уровня L за время Δt изменится объем сырья V на ΔV:

Введем безразмерные величины:

Подставим в (2.11):

Исходя из формулы (2.2):

Подставим (2.7) в (2.13) и разделим на (2.14):

Начальные условия:

Преобразуем по Лапласу с учетом (2.17):

Тогда передаточная функция по каналу управления:

По каналу возмущения:

2.5 Анализ существующих нелинейностей

Контур регулирования считают линейным, если его динамический коэф­фициент передачи постоянен, независимо от того, применяются ли в контуре только линейные элементы или он содержит также и нелинейные элементы, специально вводимые для компенсации других нелинейностей процесса.

В нелинейных контурах регулирования динамический коэффициент передачи изменяется прямо или обратно пропорционально изменению амплитуды колебаний. В случае прямой зависимости малые возмущения гасятся в меньшей степени, чем большие. Устой­чивость работы такого контура обусловливается величиной произ­ведения его коэффициента передачи на амплитуду возмущающего воздействия. Если коэффициент передачи такого контура превышает 1, то последний будет совершать незатухающие колебания.

При исследовании контура, содержащего нелинейный элемент, используют диаграмму «вход—выход». Она представляет собой график изменения динамических коэффициентов передачи объекта и регулятора в течение одного периода колебаний контура регулирования. Кривая изменения регулирующего сигнала является как бы волной, образованной отражением сигнала от статических характеристик поочередно объекта и регулятора.

Амплитуда предельных колебаний контура в общем случае зависит от коэффициента передачи объекта регулирования при периоде его собственных колебаний. Определив этот коэффициент, можно построить диаграмму «вход—выход» или диаграмму изменения амплитуды колебаний в зависимости от коэффициента передачи, а затем найти амплитуду предельных колебаний.

Нелинейные элементы бывают трех типов:

1) относятся элементы с непрерывной нелинейной функцией, в качества примера которой можно привести характеристику перемещения плунжера регулирующего клапана;

2) элементы с кусочно-ломаной функцией, например элементы систем регулирования, работающие в режиме насыщения;

3) элементы, обладающие динамической нелинейностью, у которых сдвиг по фазе и величина коэффициента передачи изменяются при изменении амплитуды входного сигнала. К последней разновидности относятся также элементы с гистерезисной характеристикой.