4. Математическая модель

Введем условные обозначения:

- количество местных студентов, обучающихся в университете (в оптимальном плане);

- количество иностранных студентов, обучающихся в университете (в оптимальном плане);

- количество местных студентов, которые могут учиться  в университете;

- общее количество студентов, которые могут учиться  в университете;

- количество преподавателей, работающих  в университете;

- количество местных студентов, приходящихся на одного преподавателя, по нормативам;

- количество иностранных студентов, приходящихся на одного преподавателя, по нормативам;

- доля местных студентов (от общего числа местных студентов), живущих в общежитии по нормативам;

- доля иностранных студентов (от общего числа иностранных студентов), живущих в общежитии по нормативам;

- плата за обучение одного местного студента;

- плата за обучение одного местного студента.

 

Тогда математическую модель задачи можно записать в виде:

Целевая функция – получение максимального дохода от обучения студентов в университете

Ограничение на суммарное количество студентов, обучающихся в университете

Ограничение на количество местных студентов, обучающихся в университете

Ограничение на количество преподавателей

Ограничение на количество мест в общежитии

Условие целочисленности

- должны получить целые значения в оптимальном плане.

Условие неотрицательности переменных

 

5. Программное обеспечение

Для решения поставленной задачи выбрана прикладная программа Microsoft Office Excel с использованием процедуры Поиск решения.

 

Первый этап. Формируем матрицу для решения задачи (страницаСтуденты).

 

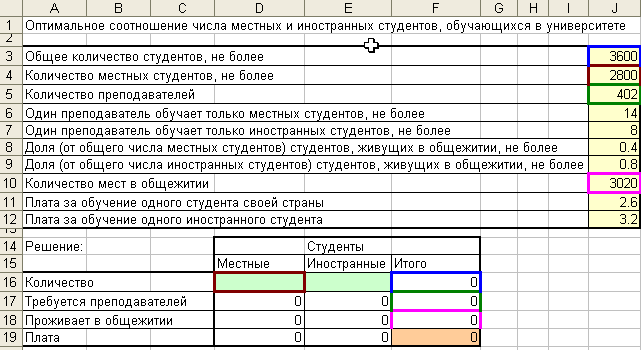
Второй этап. Записываем формулы в ячейки решения.

 

Третий этап. Заполняем шаблон <Сервис, Надстройки, Поиск решения>.

 

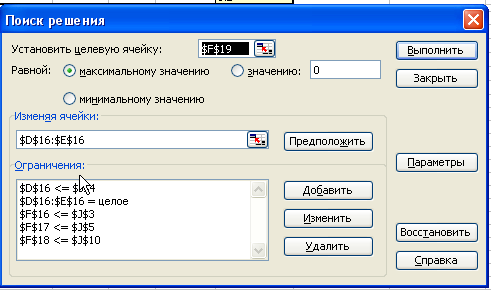
Четвертый этап. Вводим значения параметров оптимизации.

 

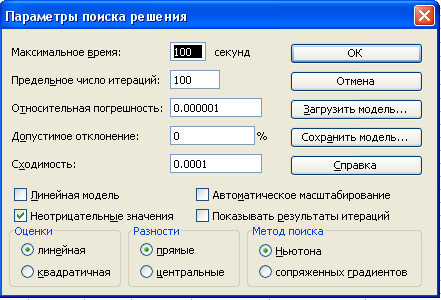
Пятый этап. Находим оптимальное решение.

 

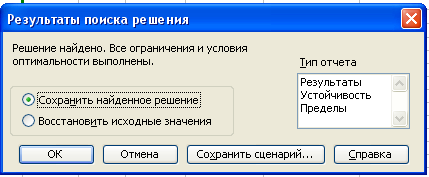
Шестой этап. Выводим отчет по результатам решения (страницаОптимальный план).

 

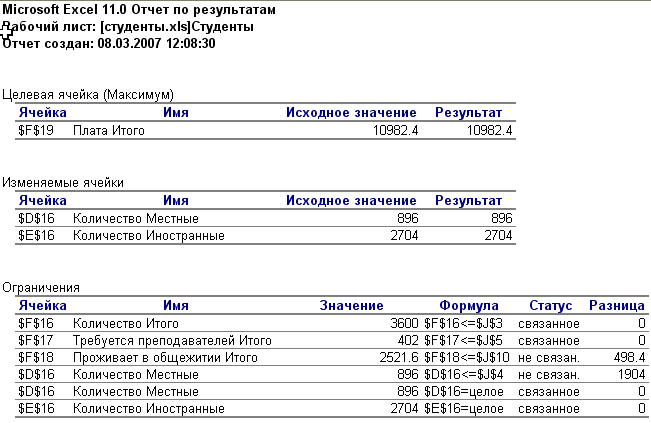
6. Анализ полученных результатов

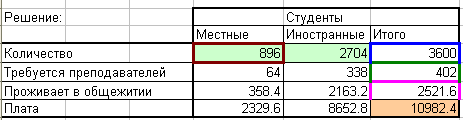
Итоговые данные помещены в исходную матрицу.

.

Для анализа полученных результатов рекомендуется использовать записанный ранее Оптимальный план, который содержит следующую информацию:

1)      В университет рекомендуется принимать 896 местных студентов (верхняя допустимая граница) и 2704 иностранных студента.

2)      Для обучения местных студентов привлекается 64 преподавателя, иностранных – 338 преподавателей, т.е. используются все преподаватели (402 человека).

3)      В общежитие можно поместить 358 местных студентов и 2163 иностранных.

4)      При выполнении указанных условий максимальный доход от обучения студентов в университете составит10982 условных единицы; при этом  доля иностранных студентов составит 78 %.

5)      Для наглядности построен график итоговых  данных (страница График).

 

  

 

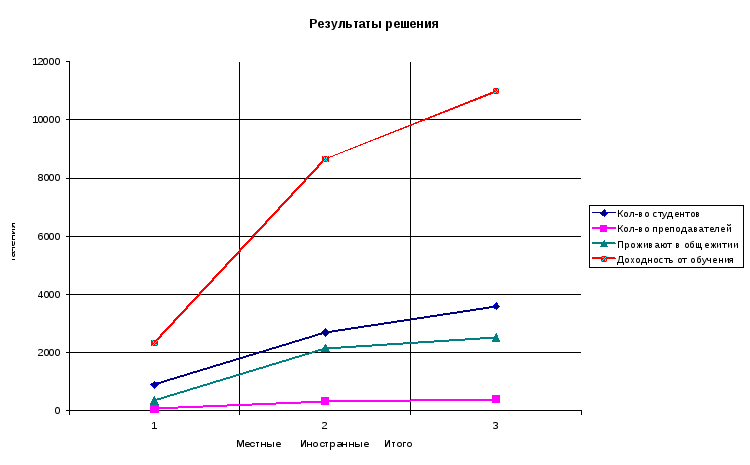
Задача записана в файл Студенты.xls.

 

7. Использованные источники

1)      Дубина А.Г. и др. Excel для экономистов и менеджеров. – СПб.: Питер, 2004.

2)       Типовые задачи менеджмента. Сайт изд-ва «Питер» (http://shop.piter.com/book...), 12.02.2007.