Затухающие колебания.

На практике всякое колебание материальной точки, которое не поддерживается извне, затухает, амплитуда его колебания уменьшается с течением времени. Причина затухания обуславливается силами, тормозящими движение, например, силой трения или силой сопротивления среды.

x

Вся система погружена в вязкую жидкость в глицерин.

Если тело движется в жидкости, то F_тр ~ V, а сухое трение не зависит от скорости.

ω₀ – частота, с которой совершались бы колебания системы в отсутствии сопротивления среды (при γ = 0) – собственная частота системы.

(2)

Решаем с помощью подстановки:

Корни уравнения:

Тогда решение (2)

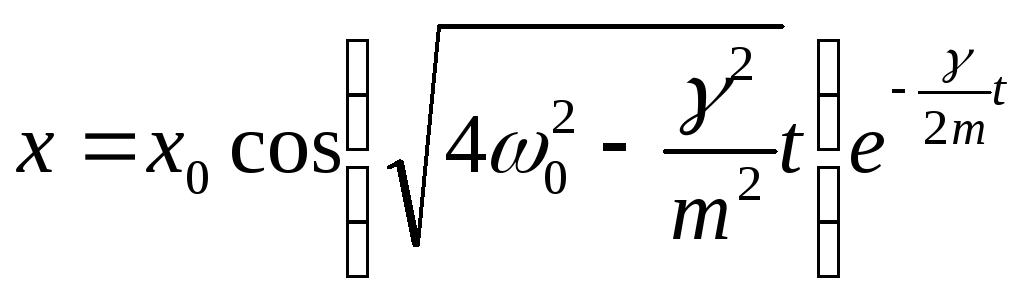
Наличие силы трения приводит к изменению частоты колебаний к затуханию их амплитуды.

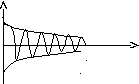х

t

- коэффициент затухания определяет скорость затухания колебаний.

- декремент затухания, т.е. характерное время, за которое амплитуда колебаний уменьшается в е раз.

Период затухания колебаний

При незначительном сопротивлении среды

Для характеристики колебательной системы используется величина

- добротность колебательной системы.

Добротность пропорциональна числу колебаний N_e, совершаемых системой за то время τ, за которое амплитуда колебаний уменьшается в е раз.

- логарифмический декремент затухания.

а(t) – амплитуда в момент времени t.

Установлено, что полная энергия колеблющейся системы пропорциональна квадрату амплитуды, следовательно, энергия системы при затухающих колебаниях:

Е₀ – значение энергии при t₀

=>

Если энергия мало изменяется за время Т, то убыль энергии за период:

Следовательно, при слабом затухании колебаний, добротность – есть отношение энергии, запасенной в системе в данный момент к убыли этой энергии за один период колебаний.

3. Волновое движение. Продольные и поперечные волны. Уравнение волны. Фазовая и групповая скорость. Длина волны и частота. Энергия волны. Сложение волн. Стоячие волны.

Пусть точка, совершающая колебания, находится в среде, все частицы которой связаны между собой. Тогда энергия колебаний точки может передаваться окружающим точкам, вызывая их колебания. Явление распространения колебаний в среде называется волной. При этом колеблющиеся частицы не перемещаются с распространяющимся Если в неограниченной среде беспрепятственно распространяется единственная волна, то она называется бегущей. Составим уравнение бегущей волны, позволяющее определять смещение любой точки волны в любой момент времени. Рассмотрим непрерывную однородную среду − струну, которая на концеx=0 присоединена к источнику гармонических колебаний в момент времени t’:D(t’)=Asint’.колебательным процессом, а колеблются около своих положений равновесия.

Если в неограниченной среде беспрепятственно распространяется единственная волна, то она называется бегущей. Составим уравнение бегущей волны, позволяющее определять смещение любой точки волны в любой момент времени. Рассмотрим непрерывную однородную среду − струну, которая на концеx=0 присоединена к источнику гармонических колебаний в момент времени t’:D(t’)=Asint’. Найдём смещение элементов струны, как функцию координаты x и времени t, то есть функцию . Очевидно, что для точкиx=0, =D(t’)=Asint’ (рис. 9.1). Предположим, что бегущее по струне в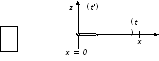озмущение распространяется с некоторой скоростью. Смещение элемента струныx в момент t равно смещению элемента x=0 в момент t’ =, если расстояние между ними равно расстоянию, которое возмущение проходит за время t-t’ со скоростью . Тогда точкиx=0 и x=x колеблются в одной фазе: x=(t-t’), ,. Поэтому уравнение бегущей синусоидальной волны == Asint’, то есть .

Преобразуем функцию . Обозначим=k и назовём его волновым числом, тогда =. Следовательно, скорость,. Величину, равную расстоянию, которое возмущение преодолевает за период колебаний, назовём длиной волны, то есть, тогда,.

Полученное уравнение и есть уравнение бегущей одномерной (или плоской) волны. При заданном x оно позволяет определить положение точки (с координатой равновесного положения x) в любой момент времени t. При заданном t оно позволяет определить мгновенные положения всех колеблющихся точек.

Таким образом, видим, что в волновом движении имеет место двоякая периодичность. С одной стороны, каждая частица среды совершает периодическое движение во времени, с другой стороны, в каждый момент времени все частицы располагаются на линии, форма которой периодически повторяется в пространстве.