Лекция 4 колебания и волны

4.1. Колебательное движение. Дифференциальное уравнение гармонических колебаний математического, физического и пружинного маятников. Амплитуда, фаза, частота и период колебаний.

Колебательным движением (колебанием) называется процесс, при котором система, многократно отклоняясь от своего состояния равновесия, каждый раз вновь возвращается к нему.

Если этот возврат совершается через равные промежутки времени, то колебание называется периодическим.

Примером колебательного движения служит гармоническое колебание.

Гармоническое колебание – это такое колебание при котором изменение колеблющейся величины со временем происходит по закону косинуса или синуса.

Колебания пружинного маятника.

x

На стержень одет шар массой m, и на него намотана пружина с жесткостью k.Запишем II закон Ньютона.

Введем

Получим дифференциальное уравнение, описывающее малые колебания. По классификации дифференциальных уравнений, принятой в математике , данное уравнение относится к дифференциальным уравнениям 2-ого порядка (старшая 2-ая производная), линейным (наша функция и ее производная входят в 1-ой степени) с постоянными коэффициентами ω₀ = const и однородным. Проверим, что общее решение данного уравнения имеет вид

Общее решение дифференциального уравнения 2-ого порядка определяется с точностью до 2-х постоянных величин. А и φ, которые должны быть определены из начальных условий.

Начальные условия определяются тем, как были созданы колебания.

Проверим, что записанная функция, действительно является решением дифференциального уравнения.

Для этого подставим ее в уравнение.

=> Данная функция является решением дифференциального уравнения.

Предположим, что колебания создаются тем, что, растянутая в начальный момент времени на х₀, пружина затем опускается.

х₀ - амплитуда колебания – максимальное отклонение от положения равновесия.

ω_0t – фаза колебания.

ω – циклическая частота колебания.

- период колебания, время одного полного колебания.

- частота колебания, число колебаний в единицу времени.

Проверим выполнение закона сохранения механической энергии при колебательном движении.

Полная энергия:

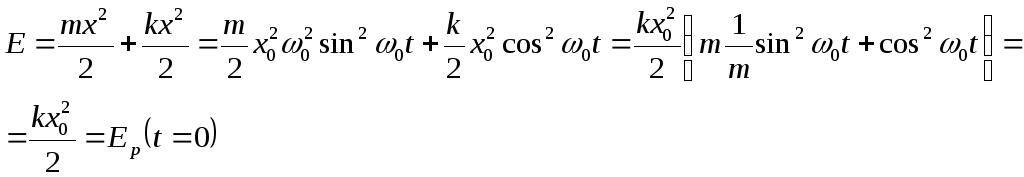
То есть сумма кинетической и потенциальной энергии не изменяется с течением времени.

T

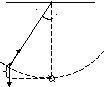
Колебания математического маятника.

Математический маятник – тяжелая материальная точка, закрепленная на невесомой нерастяжимой нити.

///////////////////////////////

_h

Воспользуемся основным уравнением динамики вращательного движения твердого тела.

- возвращающий момент

Для малых углов отклонения

Проверим выполнение закона сохранения энергии.

_.

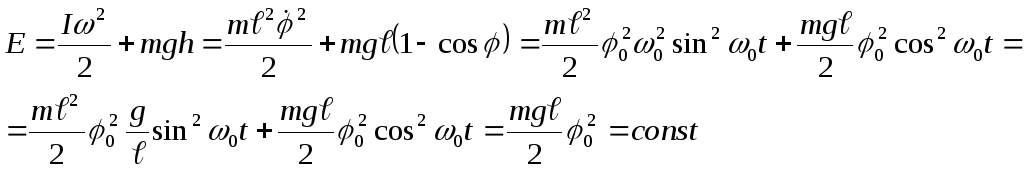
1. Вынужденные колебания. Резонанс. Затухающие колебания. Декремент затухания. Добротность.

Вынужденными называются колебания, происходящие под действием вешней периодической силы.

x

(1)

Данное уравнение относится к неоднородным дифференциальным уравнениям.

Найдем частное решение данного уравнения.

Имеем решение в виде.

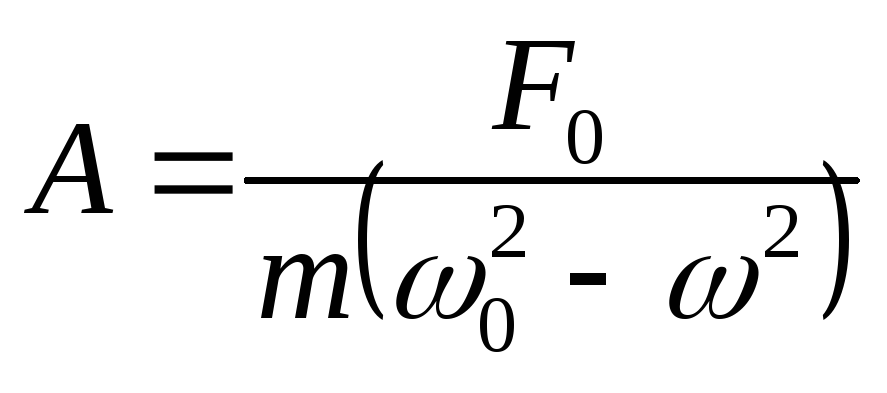
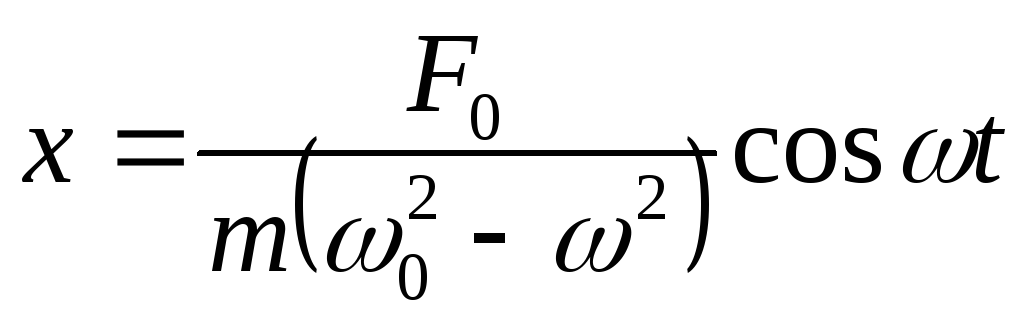
Вынужденные колебания проходят с частотой внешней вынуждающей силы. Из полученного решения видно, что при ω → ω₀, амплитуда вынужденных колебаний → ∞. Данное явление носит название явления резонанса.

Явлением резонанса называется резкое возрастание амплитуды вынужденных колебаний, возникающее при приближении частоты внешней вынуждающей силы к собственной частоте колебаний системы.

Бесконечная амплитуда получается вследствие неучета силы трения, действующей в системе. Реально, амплитуда колебаний становится большой, но не бесконечно большой. Иногда амплитуда вынужденных колебаний становится столь большой, что система подвергается разрушению.

Пример: солдаты идут по мосту, им необходимо идти не в ногу.