Законы Ньютона.

1.Тело находится в состоянии покоя или равномерного прямолинейного движения, если на него не действуют никакие силы или действие всех сил скомпенсировано.

Система отсчета, в которой выполняется I Закон Ньютона, называется инерциальной.

2.Ускорение, приобретенное телом под действием силы прямопропорционально величине этой силы и обратно пропорционально массе тела.

3.Тела действуют друг на друга с силами, равными по величине и противоположными по направлению.

2.2. Импульс тела и импульс силы. Закон сохранения импульса для системы тел. Системы замкнутые и открытые. Центр массы системы тел.

Большое значение для механики играют сохраняющиеся величины.

В механике существует 3 закона сохранения.

1.Закон сохранения импульса

2.Закон сохранения момента импульса

3.Закон сохранения энергии.

- импульс материальной точки.

Пусть имеется система из N материальных точек, взаимодействующих друг с другом, а также находящихся в каком-нибудь внешнем силовом поле. Например, система заряженных шариков, взаимодействующих друг с другом по закону Кулона, находящаяся во внешнем гравитационном поле Земли.

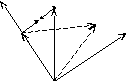
m_i m₁

mN

O

- внешняя сила, действующая на 1-ую материальную точку.

- сила, действующая со стороны 2-ого тела на первое, а - сила, действующая со стороны 1-ого тела на 2-ое.

Запишем систему уравнений движения для nел. Входящих в систему. Всего N – уравнений движения.

+

………………..

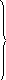
Введем

- полный импульс системы

- полная внешняя сила, действующая на систему

Если на систему е действуют никакие внешние силы, или векторная сумма всех вешних сил = 0 (), то, откуда следует, что=const.

Таким образом, мы показали, что полный импульс системы материальных точек не изменяется с течением времени при выполнении заданного выше условия.

Понятие центра масс системы материальных точек.

разделим на полную массу системы и домножим

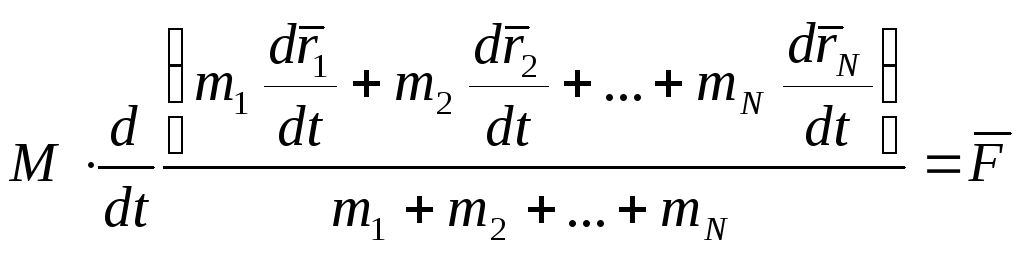
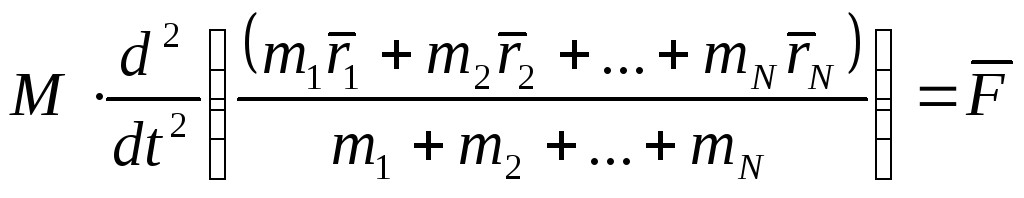
(1)

Вводим в рассмотрение точку, положение которой в пространстве определяется . Данная точка называетсяцентром масс системы.

- ускорение центра масс

- скорость центра масс

Таким образом, мы показали, что под действием внешних сил вся механическая система движется, таким образом, как одна материальная точка с массой равной суммарной массе системы и помещенной в центр масс.

Таким образом, движение системы материальных точек может быть представлено как поступательное движение центра масс и движение всех точек системы относительно центра масс.

Если на систему не действуют никакие внешние силы или их действие скомпенсировано, то центр масс системы покоится или движется равномерно прямолинейно.

2.3. Работа и мощность. Кинетическая и потенциальная энергия. Закон сохранения энергии.

1. Кинетическая энергия.

умножаем на

(2)

О (1)

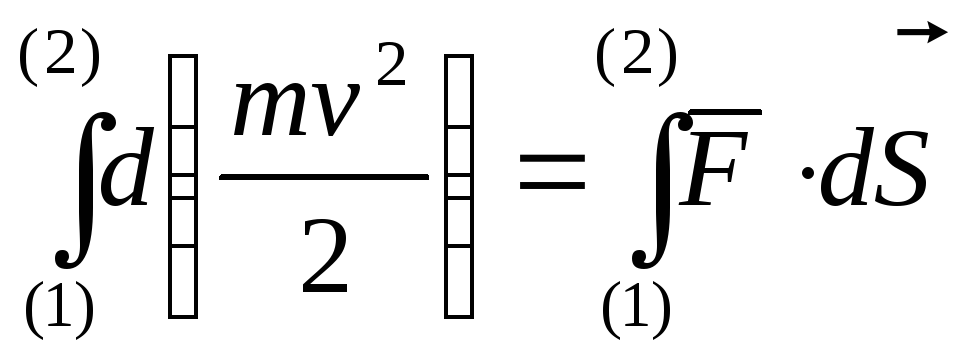
- кинетическая энергия материальной точки

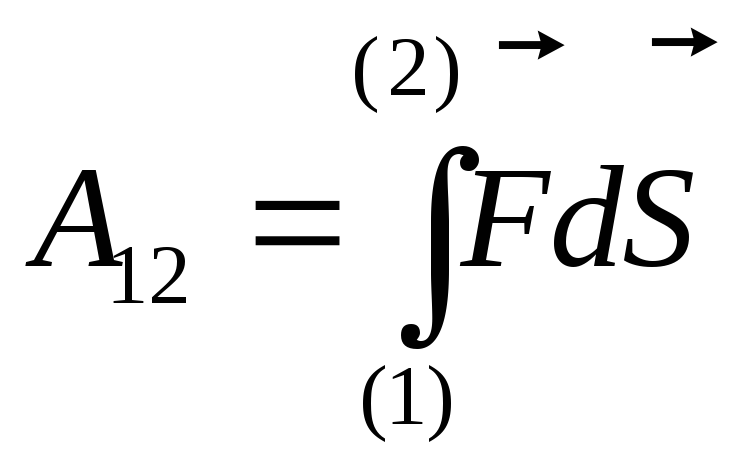- работа, совершенная силой F₁, при перемещении материальной точки из начальной т.1 в конечную точку траектории (2).

- мгновенная мощность силы F.

- мощность – работа, совершаемая в единицу времени

;

2. Потенциальная энергия.

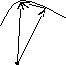
Движение материальной точки в поле силы тяжести. Материальная точка перемещается из точки (1) в точку (2) по произвольной траектории. Вычислим работу совершаемой силой тяжести при перемещении точки из 1 в 2.

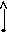h

(2)

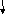
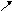
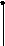
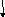
(1)

/////////////////////////////////////////////

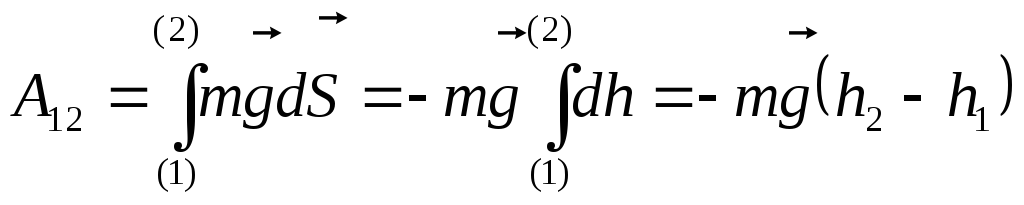
Проекция на ось h.

Таким образом, показано, что работа, совершаемая силой тяжести. не зависит от формы траектории, а определяется лишь положением начальной и конечной точки траектории.

Кроме того может быть введено в рассмотрение функция U называемая потенциальной энергией, такая, что работа определяется разностью значений этой функции в начальной и конечной точке траектории.

Величина равная сумме кинетической и потенциальной энергии материальной точки называется полной энергией и сохраняется при движении материальной точки вдоль траектории.