Лекция 6.

6.1. Основное уравнение молекулярно-кинетической теории газов для давления. Распределение Максвелла-Больцмана молекул газа по скоростям.

Рассмотрим упрощенную модель газа. Вводится 2 упрощения.

1.Все молекулы движутся с одной и той же скоростью.

2.Все молекулы газа движутся только в направлениях перпендикулярных к стенкам сосуда.

Рассмотрим газ, находящийся в сосуде, имеющего форму параллелепипеда. Необходимо вычислить давление газа, оказываемое на стенку.

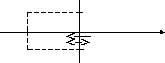vΔt

ΔS

2p=Δp₁

p

Молекулы, которые за время Δt могут столкнуться с участком ΔS, находятся внутри цилиндра, высота которого равна vΔt.

Вычислим число ударов молекул с участком ΔS за время Δt.

- число молекул внутри цилиндра

всех молекул движущихся в направлении стенки (т.к. стенок всего 6)

Рассмотрим одно столкновение. Импульс р, а изменение импульса молекулы при упругом ударе о стенку составляет 2р. 2p=Δp₁

Запишем импульс, переданный стенке за время Δt.

Тогда сила, действующая на участок ΔS

Давление

- давление

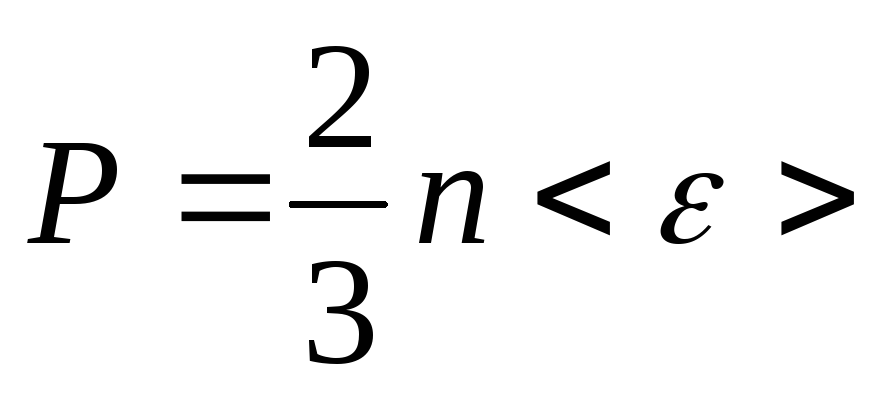- основное уравнение МКТ газов

если поводить точный расчет (без упрощений)

- средняя кинетическая энергия одной молекулы.

Оно связывает между собой макропараметры газа (Р - давление) и микропараметры () газа.

m₁ – масса одной молекулы

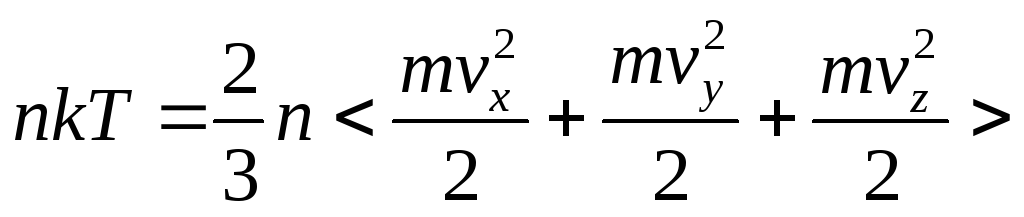
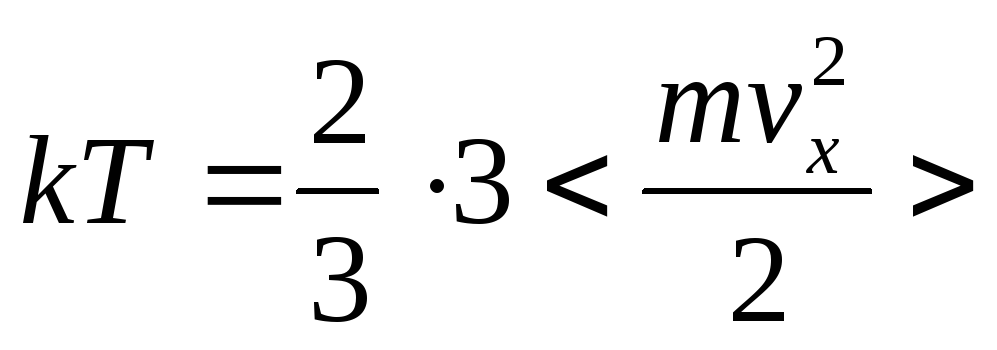
Распределение Максвелла. Распределение молекул по скоростям.

Скорости молекул идеального газа неодинаковы и подчиняются определённым закономерностям, имеющим статистический характер. Найти закон распределения молекул по скоростям – это значит определить число молекул dn, скорости которых находятся в заданном интервале скоростей от v до v +dv. Опираясь на формулу Больцмана, найдём, как распределены молекулы идеального газа по скоростям. Задачу решим для идеального газа, находящегося в состоянии теплового равновесия.

Рассмотрим вертикальный столб газа с основанием в 1 м², находящийся в однородном поле силы тяжести. Направим ось z вверх и вначале найдём распределение молекул по значениям лишь компоненты скорости v_z. Пусть n₁ – полное число молекул в 1 м³ газа, а функция f(v_z) определяет долю числа молекул с данным значением компоненты скорости v_z. Тогда число молекул в 1 м³ газа со значениями этой компоненты скорости, лежащими в интервале от v_z до v_z+dv_z равно

.

Функция f(v_z), собственно, и определяет распределение молекул по v_z. Она называется функцией распределения молекул по компоненте скорости v_z.

Согласно формуле (4), число молекул на высоте z = h меньше их числа на высоте z = 0. Причину этого легко указать: все те молекулы, для которых составляющая скорости v_z недостаточно велика, не могут достичь высоты h. Для того чтобы какая-то молекула могла достичь этой высоты, она должна, двигаясь снизу вверх, пересечь плоскость z = 0 со скоростью v_z, удовлетворяющей условию

.(7)

Скорость, соответствующую здесь знаку равенства, обозначим v_h. Все молекулы, удовлетворяющие этому условию, пересекут также с некоторой скоростью v_z ≥ 0 плоскость z = h. Число молекул, достигающих с некоторой скоростью v_z = 0 > 0 плоскость z = 0, обозначим n(0).

Мы считаем, что температура во всём столбе газа одинакова. Соответственно распределение молекул по скоростям на всех высотах также одинаково. Отсюда, принимая во внимание полную беспорядочность движения, можно заключить, что число молекул, пересекающих горизонтальную плоскость на том или ином уровне, пропорционально числу молекул на этом уровне.

Используя формулу , находим

.

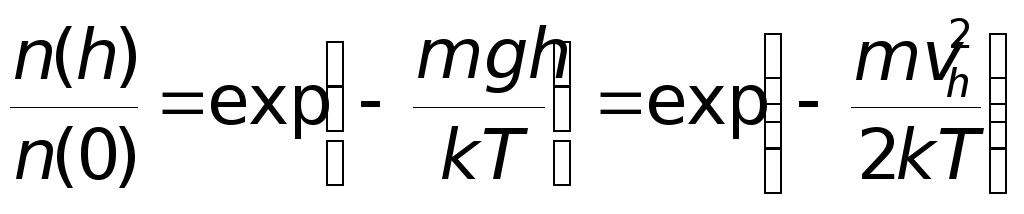Выразим теперь число n(h) (т.е. число молекул, пересекающих плоскость z = h со скоростью v_z ≥ 0 и плоскость z = 0 со скоростью v_z ≥ v_h) через функцию распределения f(v_z). Нас интересует число молекул, прошедших через плоскость z = 0 снизу вверх за 1 с. Если v_z – скорость молекул в вертикальном направлении, то число молекул, пересекающих рассматриваемую плоскость с такой же скоростью за 1 с, очевидно, равно числу молекул с этой скоростью в столбе газа с высотой v_z, т.е. равно . Полное число молекул, пересекающих плоскостьz = 0 со скоростями v_z ≥ v_h, определится интегралом от полученного выражения в пределах от v_h до ∞, т.е.

.

.

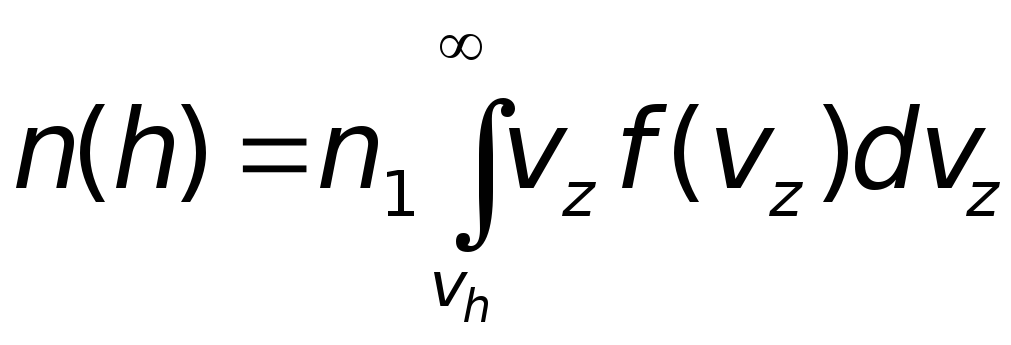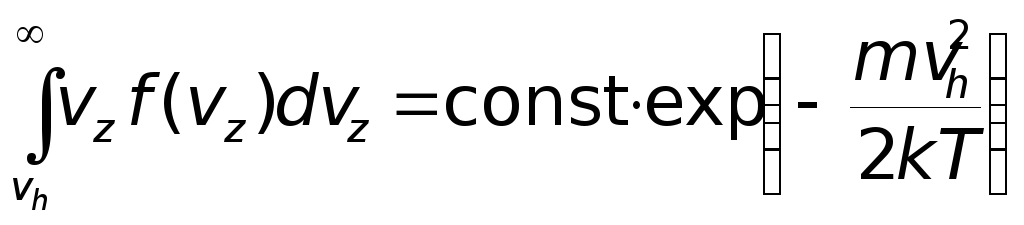Продифференцировав это выражение по v_h и выполнив несложные вычисления, находим

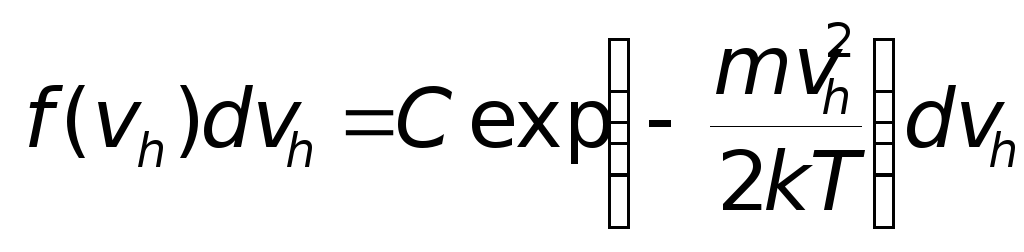
(множитель dv_h в правой и левой частях подчёркивает, что мы имеем дело с распределениями). Поскольку h – произвольная высота, то мы вернёмся теперь к исходным обозначениям и заменим v_h на v_z. Из определения функции f(v_z) следует, что

.

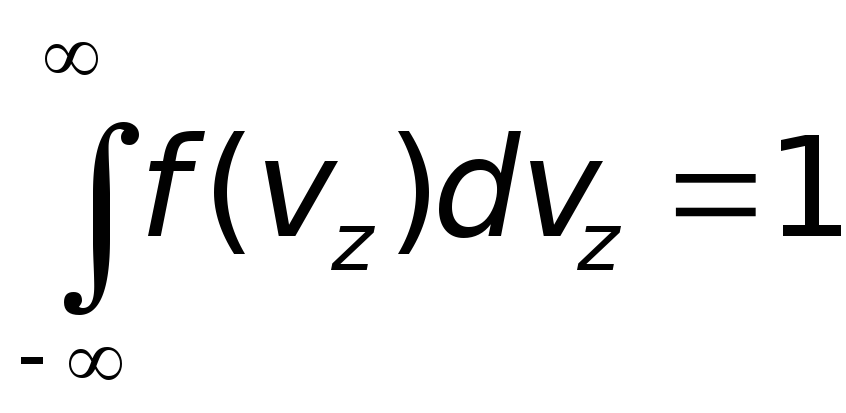Для определения постоянной С, воспользуемся тем, что

.

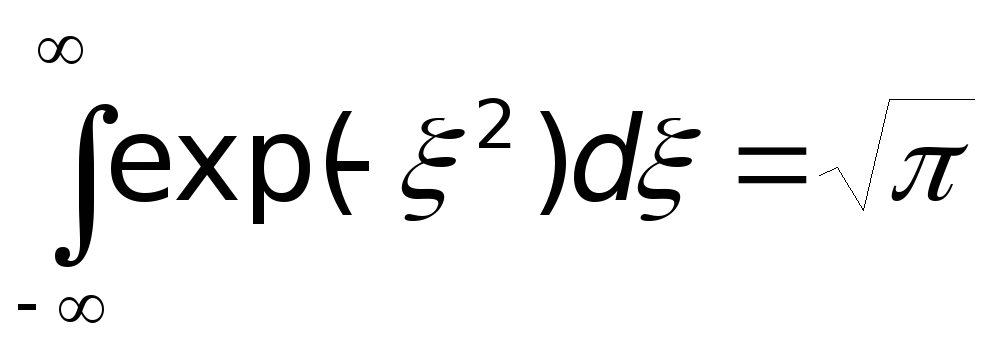Из этих соотношений следует, что и, следовательно

.

Итак, мы нашли искомую функцию, описывающую распределение молекул по вертикальной компоненте скорости.

Мы нашли распределение молекул по значениям одной определённой компоненты их скорости. Вследствие полной беспорядочности движения точно такие же выражения справедливы и для других компонент скорости.

Формулу можно преобразовать так, чтобы она давала распределение молекул по абсолютной величине скорости. Эта задача была решена Максвеллом, который показал, что число молекул dn, скорости которых лежат и интервале скоростей от v до v +dv определяется соотношением:

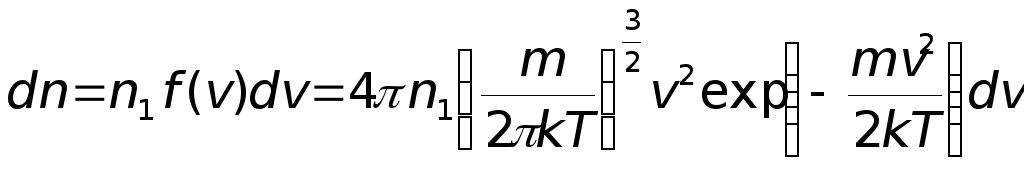
Соотношение называется распределением Максвелла по абсолютным значениям скорости.

Вид распределения (приведён на рисунке для двух температур. При v = 0 f(v) = 0, при v₀ эта функция достигает максимума и очень быстро стремится к нулю с дальнейшим возрастанием скорости. Более пологая кривая отвечает более высокой температуре, но площади под обеими кривыми одинаковы и в соответствии с соотношением равны 1. Максимум кривой соответствует скорости 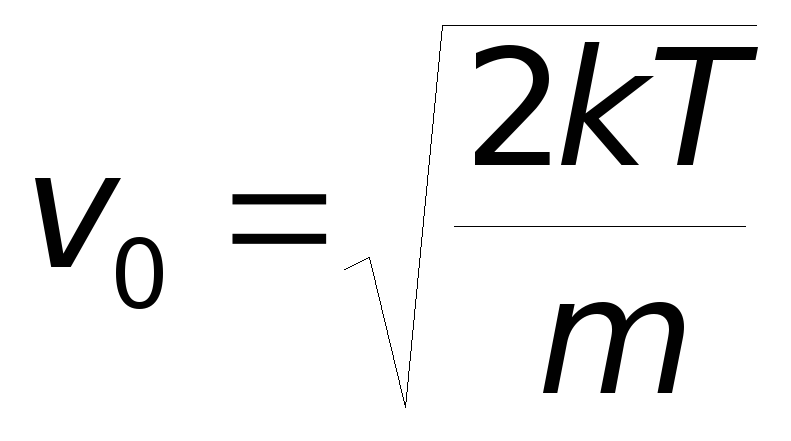, которая называется наиболее вероятной скоростью движения молекул. Из соотношения дляv₀ следует, что с увеличением температуры газа его наиболее вероятная скорость увеличивается. При этом, доля медленных молекул газа уменьшается, а доля быстрых молекул растёт.