Замечание.
Уравнение (24) справедливо, если справедлива
производная
.
Уравнение (24) является дифференциальным
уравнением частных производных только
относительно водонасыщенности.
Введем безразмерные переменные:
поровый объем - Vпор = L·B·h·m, где
L – характерный линейный участок пласта от линии нагнетания до линии отбора.
В – ширина полосы нагнетания
L – расстояние между рядами 300-700 м (нефт.) и 1000-1500 м (газ.)
0 ≤ х ≤ L
Если введем безразмерную переменную
,
получим безразмерную величину, которая
меняется от 0 до 1.
Замечание.
можно рассматривать, как объем пласта
между начальным (нагнетания) х = 0 и
конечным сечением (линия отбора) х = l,
выраженного в долях порового объема.
Введем переменную:
(25)
Замечание.
τ отражает объем жидкости закаченной (отобранной) в (из) пласт к моменту времени t, иными словами τ характеризует количество прокаченных (отобранных) поровых объемов. u (λ) есть движение точки (·), когда u(λ)Bh = q(λ) есть уже дебит (отбор) на линии отбора.
Возвращаемся к уравнению (24):
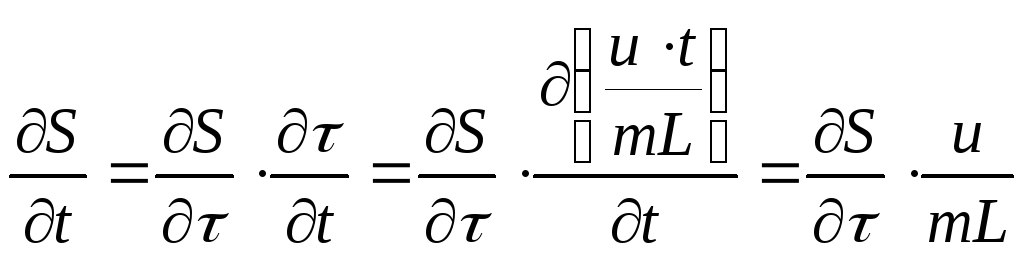(26)
(27)
Подставляем эти выражения в (22):
- основное уравнение Баклея-Леверетта
в безразмерном виде (28)
F = F (S; ξ) – функция насыщенности и безразмерного расстояния
(29)
(29) – гиперболическое уравнение первого порядка относительно водонасыщенности S.
S
(0, τ) ׀ ξ=0
= S* - граничное
условие
S (ξ, 0) ׀ τ=0 = S* - начальное условие (30)
F (S) ׀ ξ=0 = 1 (см.график ф-ции Баклея-Леверетта)
Замечание.
При ξ = 0, т.е. на линии нагнетания, насыщенность S* все занято водой на линии нагнетания, т.е. насыщенность S = 1. При τ = 0, за исключением зоны нагнетания, где все заполнено нефтью, кроме пор, в которых находится вода.
τ 
ξ = ξ (τ)
ξ
- это некоторая линия на плоскости
безразмерных переменных
.
При этом насыщенность S
в процессе нагнетания будет меняться
вдоль направления движения флюидов
.
S = S
В этом случае:
dS =
(31)
Сравним (31) и (29):
-
dS = 0
тогда (31) можно записать:
(
)
Теперь сравним (
)
и (29):
F/(S)
=
(32)
Из сравнения уравнений (29) и (
)
следует, что F/(S)
=
.
Замечание. Уравнение (32) означает, что насыщенность S остается постоянной вдоль линии движения флюидов ξ = ξ (t), а сами линии ξ называются изосатами (линии одинаковой водонасыщенности).
τ ξ (S*; τ)
ξ
(S1;
τ)
нагн.скв.
ξ
(S2;
τ)
ξ
(S3;
τ)
доб.скв
0
ξ
(S*;
τ)
ξ (S; τ)
S* > S1> S2 > S3 > S*
Если рассматриваемая характеристика выходит из начальной точки (ξ0; 0), то значение водонасыщенности S на этой характеристике (изосате) остаётся равной начальному значению.
S (ξ0; 0)=φ (ξ0)
Т.о. ξ (S; τ) являются траекториями распространения постоянных значений насыщенности S.
Вернемся к уравнению (
),
продифференцировав его по dτ:
=>
(
)
Из сравнения (29) и (
):
(33)
Проинтегрируем (32):
Подставим начальные и граничные условия:
τ=0
ξ = с = ξ0 =>
ξ =
· τ + ξ0
(35)
ξ (S, 0) = ξ0 (S) = 0
при S > S*
- частное решение уравнения (29)
(36)