
09-01-2015_09-46-11 / Лекция 6. ТВ и МС
.pdfЛекция 6.
Схема Бернулли. Формула Бернулли. Поведение вероятностей биномиального распределения.
5.1. Схема Бернулли
Пусть в результате некоторого случайного испытания ( эксперимента ) может произойти (успех) или не произойти (неудача) событие А. Испытание повторяется n раз. При этом выполняются следующие условия :
1)каждое испытание имеет два исхода , называемые успех и неудача; это взаимно несовместные и противоположные события;
2)вероятность успеха Р(А)=р в каждом испытании остается постоянной. Вероятность неудачи q = 1-p
3)все n испытаний – независимы, т.е. результат любого испытания не зависит от исхода в предыдущих испытаний.
Тогда такая последовательность независимых испытаний с двумя исходами (успех /неудача) называется испытаниями Бернулли или схемой Бернулли.
Пример. Монету подбрасывают n раз, успехом считается выпадение «Г». Вероятность успеха при каждом испытании р=Р(Г)=1/2
Пространство элементарных событий каждого отдельного испытания состоит
из двух точек |
Ωi ={ω0 , ω1 }, |
i=1,2,…,n |
|
|
ω0 =0 (неудача), |
ω1 =1(успех) |
|
||
p(ω1)=p , |
p(ω0)=1-p = q |
|
|
|
Пространство элементарных событий n испытаний Бернулли содержит 2n |
||||
точек: N(Ω )=2n |
|
|
|
|
Ω = {ω : ω =(a1 , a2 ,…,an ) , ai =0,1} |
|
|
||
Если общий элементарный исход включает k успехов и (n-k) |
неудач, то в силу |
|||
независимости испытаний |
|
|
||
p(ω )=pk qn-k , |
k= a1 + a2 +…+an |
|
||
Число таких исходов совпадает с числом способов, которыми |
можно расставить |
|||
k единиц на n |
местах, не учитывая порядок, в котором их расставляют. Число |
таких способов |
равно Cnk . Следовательно, вероятность Pn (k) того, что в n |
испытаниях Бернулли произошло k успехов равна
8)Pn (k) =Cnk pk qn-k
Выражение (4.8) называется формулой Бернулли Пример. В урне 3 белых и 2 черных шара. Из урны 4 раза наугад вынимают
по 2 шара и возвращают обратно. Найти вероятность того, что : а) ровно 3 раза вынули шары разного цвета; в) хотя бы один раз вынули шары разного цвета.
Решение.
а) N=C52=5!/2!3!=4 5/2=10 N(A)= 3 2=6
P4(3)=C43 p3 q1 =4(0,6)3 (0,4)=0,3456
32
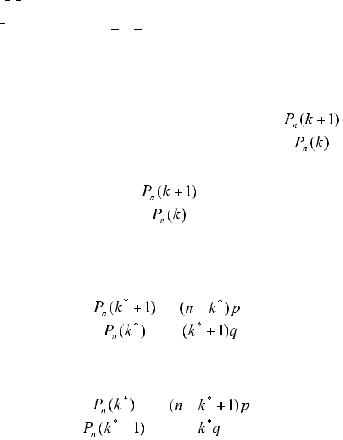
в) Событие «хотя бы один раз успех» противоположен событию «ни разу не было успеха»
P4 (1)+P4 (2)+P4 (3)+P4 (4)= 1-P4(0)=1-q4 =1-(0,4 )4 =0,9744
Пример. Студент пишет контрольную работу по теории вероятностей. У него есть предложение о том, как решить задачу, однако свои способность найти правильное решение студент оценивает невысоко - примерно числом 0,4. Вокруг студента в аудитории сидят 5 однокурсников. Можно рискнуть опросить их и
принять либо отвергнуть |
решение на основании большинства голосов. |
|
Подготовку этих |
однокурсников студент оценивает так же , как и свою. Как |
|
лучше поступить студенту |
– положиться на свои соображения или на |
|
большинство голосов однокурсников ? |
||
Решение. |
р=0,4 – вероятность правильного решения , k=3,4,5; n=5 |
|
P5 (3) +P5 (4) +P5 (5) = 0,317
Вероятность снизиласьпоэтому лучше решать самому.
Максимальная вероятность
Найдем число успехов k* , вероятность которого самая большая среди всех вероятностей Pn (k) . Рассмотрим отношение
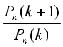 =
= 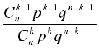 =
=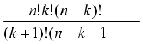
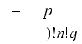 =
=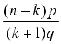
При изменении k от 0 до n члены Pn (k) сначала монотонно возрастают, затем монотонно убывают, достигая наибольшего значения при k* ( смотри рисунок)
Следовательно, если Pn (k) монотонно возрастает, то |
|
>1, и |
||||||||||||||||||
|
||||||||||||||||||||
|
|
|
Pn (k+1) > Pn (k) |
|
|
|
|
|||||||||||||
если Pn (k) монотонно убывает , то |
|
|
|
|
|
|
|
|
<1 , |
|
|
и |
|
|||||||
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
Pn (k+1) < Pn (k) |
|
||||||||||||||||
Поэтому для k* выполняются неравенства : |
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
= |
|
|
|
|
|
|
|
≤ 1, |
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
которое выполняется при |
k* |
|
≥ np-q |
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
= |
|
|
|
|
|
|
|
|
|
≥ 1, |
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
которое выполняется при |
k* |
|
|
|
|
np + q |
|
|
|
|
||||||||||
|
≤ |
|
|
|
|
|
||||||||||||||
объединив последние два неравенства получим, что
33
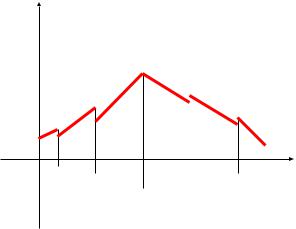
np-q ≤ k* ≤ np + q
p |
|
|
k*-1 k* |
k*+1 |
k |
Будем называть Pn (k* ) максимальной вероятностью . Число k* называют
наиболее вероятным числом успехов.
Пример. Вероятность изготовления на автоматическом станке стандартной детали равна 0,8. Найти вероятности возможного числа появления бракованных деталей среди 5 отобранных. По данным примера найти наивероятнейшее число появления бракованных деталей из 5 отобранных и вероятность этого числа.
Решение. |
Вероятность изготовления бракованной детали p=1-0,8 |
|||
I способ |
Искомые вероятности находим по формуле Бернулли : |
|||
P5 (0)=0,32768 |
|
|
||
P5 (1)=0,4096 |
|
|
||
P5 (2)=0,2048 |
|
|
||
P5 |
(3)=0,0512 |
|
|
|
P5 |
(4)=0,0064 |
|
|
|
P5 |
(5)=0,00032 |
|
|
|
II |
способ |
по формуле максимальной вероятности |
||
5 0,2-0,8 |
≤ k* ≤ 5 0,2+0,2 |
, |
0,2 ≤ k* ≤ 1,2 , |
|
k* =1 , |
P5 (1)=0,4096 |
|
|
|
Пример. В среднем 20% пакетов акций на аукционах продаются по первоначально заявленной цене. Найти вероятность того, что из 9 пакетов акций в результате торгов по первоначально заявленной цене :
1)не будет проданы 5 пакетов
2)будет продано а) менее 2 пакетов
б) не более 2 в) хотя бы 2 пакета
г) наивероятнейшее число пакетов.
Решение.
34
1) |
p = 1 – 0,2 = 0,8 , успех – не будет продано. |
P9 (5) = 0,066 |
2) |
p= 0,2 , успех – будет продано |
|
a) |
P ( k < 2) = P9 (0) + P9 ( 1) = 0,436 |
|
б)P ( k ≤ 2 )= P9 (0) + P9 (1 ) + P9 (2) = 0,738
в) P ( k ≥ 2 ) = P9 (2 ) + P9 ( 3 ) + …+ P9 (9 ) = 1 – P ( k < 2 ) = 1 – 0,436 = 0,564
г) |
P= 0,2 ; q = 0,8 |
9 0,2 – 0,8 ≤ k* ≤ 9 0,2+ 0,2 |
; |
|
1 |
≤ k* ≤ 2 ; |
k* |
= 1 ; 2 - два целых числа |
, поэтому |
|
Pнаив |
= P9 (1 ) + P9 (2 ) = 0,604 |
|
|
35
