
09-01-2015_09-46-11 / Лекция 7. ТВ и МС
.pdf
Лекция 7.
Локальная и интегральная теоремы Муавра –Лапласа. Схема серий и приближенная формула Пуассона.
|
|
|
|
|
Формула Пуассона |
|
|
|
Теорема Пуассона . |
Если вероятность р наступления события А |
в каждом |
||||||
испытании |
стремится к 0 ( р |
|
→ 0 ) при неограниченном увеличении числа |
n |
||||
испытаний ( n →∞ ) |
причем произведение np стремится к постоянному числу λ |
|||||||
( np →λ ) |
, то вероятность |
|
Pn (k) того, что событие А появится |
k раз в |
n |
|||
независимых испытаниях удовлетворяет предельному неравенству : |
|
|
||||||
( 4.9) |
Pn (k)= Pk (λ) = |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|||
Доказательство. Pn (k) = 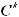 pkqn-k =
pkqn-k = 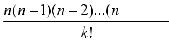
 pk(1-p)n (1 –p)-k
pk(1-p)n (1 –p)-k
Учитывая , что 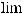 np = λ имеем p ≈
np = λ имеем p ≈ 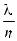
Pn (k)≈ 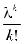 (1 (1 -
(1 (1 -  )(1-
)(1- 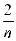 )…(1 -
)…(1 -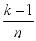 ))(1 -
))(1 -  )n ( 1-
)n ( 1- 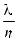 )-k
)-k
Так как
 (1 -
(1 -  )=
)=  (1-
(1- 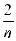 )=…=
)=…= (1 -
(1 -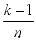 ) = 1
) = 1
 (1 -
(1 -  )n =
)n = 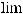

 = e-λ
= e-λ
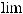 ( 1-
( 1-  )-k = 1
)-k = 1
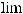 Pn (k)=
Pn (k)= 
Строго говоря , условие теоремы Пуассона p → 0 при n →∞ так что np →λ противоречит исходной предпосылке схемы испытаний Бернулли, согласно которой вероятность наступления события в каждом испытании р =const . Однако , если вероятность р – постоянна и мала , число испытаний n – велико и число λ = np - незначительно ( будем полагать, что λ = np ≤ 10 ), то из предельного равенства (4.9) вытекает приближенная формула Пуассона :
Pn (k) ≈  = Pk (λ)
= Pk (λ)
В таблице приложений приведены значения функции Пуассона.
Вероятность события , заключающегося в том, что А появится не более m раз , вычисляется по формуле :
32

P(k ≤ m ) ≈ 


Пример. Известно, , что при транспортировке и разгрузке керамической отделочной плитки повреждается 2,5 % . Найти вероятность того, что в партии из 200 плиток поврежденными окажется а) ровно 4 , б) не более 6.
Решение. p=0,025мало , n = 200 - велико λ = np= 5 < 10 можно воспользоваться формулой Пуассона
P200 (4) ≈ 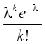 =
=  e-5 =0,1755
e-5 =0,1755
P200 (k ≤ 6 ) ≈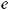

 = e-5
= e-5  = 0,7622
= 0,7622
Пример. В новом микрорайоне поставлено 10000 кодовых замков на входных дверях домов. Вероятность выхода из строя одного замка в течение месяца равна 0,0002. Найти вероятность того, что за месяц откажут два замка.
Решение. В нашем случае λ = np=10000 0,0002 =2 < 10
используем формулу Пуассона
Р10000(2)=22 е-2 /2!=0,27
Формулы Муавра – Лапласа
При достаточно большом n и не слишком малых p и q формула Пуассона уже дает значительную погрешность и применяется другое приближение – формула Муавра-Лапласа.
Локальная теорема Муавра – Лапласа . Если в схеме Бернулли число испытаний n велико , то для всех k справедлива приближенная формула :
|
Pn (k) |
≈ |
|
|
|
|
|
|
|
|
|
ϕ (x), |
||||
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|||||||||||
где |
ϕ(x) = |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
и , |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x = |
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|||||||||
Значения функции ϕ( x) для некоторых х приведены в таблице. Так как |
||||||||||||||||
функция ϕ( x) |
является четной, то при определении ϕ( x) для отрицательных х |
|||||||||||||||
нужно воспользоваться равенством |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ϕ( - x) = ϕ( x) |
|||||||||||||||
Пример . В некоторой местности |
|
|
|
из каждых 100 семей 80 имеют |
||||||||||||
холодильник |
. Найти вероятность |
того, что из 400 семей 300 имеют |
||||||||||||||
холодильники. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Решение. p = 80/100 =0,8 , n = 400 , np = 400 0,8 = 320 > 10
33
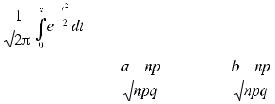
Следовательно, используем локальную теорему Муавра – Лапласа x = ( 300 – 400 0,8)/√(400 0,8 0,2) = ( 300 – 320 )/√64 = - 20/8=-2,50 P400 (300) ≈( 1/√64 ) ϕ( -2,50 )= 0,0175/8 = 0,0022
Пусть в условиях примера необходимо найти вероятность того, что от 300 до 360 семей ( включительно ) имеют холодильники . Тогда по теореме сложения вероятностей имеем
P400 ( 300 ≤ k ≤ 360 ) = P400 (300 ) + P400 (301 ) + …+ P400 ( 360 )
В принципе вычислить каждое слагаемое можно в отдельности по локальной теореме Муавра – Лапласа, но большое количество слагаемых делает расчет весьма громоздким. В таких случаях используется следующая теорема
Интегральная теорема Муавра – Лапласа
Если в схеме Бернулли число испытаний n велико , то для вероятности того, что число успехов k будет не менее a и не более b справедливо приближенное равенство
Pn ( a ≤ k ≤ b ) ≈ Ф0 (х2 ) – Ф0 (х1 ),
где |
Ф0 (х) = |
|
|
|
|
|
|
|
функция Лапласа |
|||||||||
|
|
|
|
|
|
|
||||||||||||
|
||||||||||||||||||
|
|
|
|
|
|
|
x1 = |
|
|
|
|
; x2 = |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
Доказательство будет приведено как следствие центральной предельной теоремы Отметим некоторые свойства функции Лапласа , которая табулирована.
Ф0 (-х) = - Ф0 (х) |
0≤ х < 5 ; |
Ф0 (х) = 0,5 |
x ≥ 5 |
Пример . В условиях предыдущего примера P400 ( 300 ≤ k ≤ 360 ) ?
Решение x1 = ( 300-400 0,8)/√( 400 0,8 0,2) = -2,50 ; x2 =( 360-400 0,8)/√( 400 0,8 0,2) = 5,0
P400 ( 300 ≤ k ≤ 360 ) ≈ Ф0 ( 5 ) – Ф0 (- 2,5 ) = 0,5 + 0,4938 = 0,9938
Пример . Вероятность того, что зашедший в ресторан посетитель сделает заказ , равна 0, 8. Определить вероятность того, что из 100 зашедших не менее 75 сделают заказ.
Решение. n=100 , p= 0,8, q= 0,2 , np = 80 > 10
P ( k ≥ 75 ) = P( 75 ≤ k ≤ 100 ) ≈ Ф0 ( 5 ) – Ф0 (- 1,2 ) =0,5 + 0,385 = 0,885
34
