
09-01-2015_09-46-11 / Лекция 8. ТВ и МС
.pdfЛекция 8 Понятие случайной величины. Закон распределения. Функция
распределения и ее свойства.
Часто исход случайного эксперимента ω выражается некоторым числом ξ. Пример. В урне 2 белых и 4 черных шара. Из урны вынимают наугад 4 шара.
Будем характеризовать исход эксперимента количеством вынутых белых шаров.
ξ =0,1,2
Если исход опыта не описывается числом, то можно провести «оцифровку» результатов случайного эксперимента.
Пример. При бросании монеты условимся , что «герб» обозначается 1, а
«цифра» - 0 . |
В этом случае эксперимент характеризуется набором чисел 0 и 1. |
||||
|
|
|
|
|
|
|
Элементарное событие |
Число гербов ξ |
Вероятность р |
|
|
|
ω |
|
|
|
|
|
Ц |
|
0 |
0,5 |
|
|
Г |
|
1 |
0,5 |
|
Когда каждому элементарному событию ставим в соответствие число, то тем
самым мы определяем некоторую числовую функцию. Так как значение этой |
|
|||||||
функции ξ есть число , определяемое |
от случая исходом эксперимента, то ее |
|||||||
называют случайной величиной. В нашем примере число гербов - случайная |
|
|||||||
величина. Строгое определение случайной величины |
основывается именно на |
|||||||
понятии функции. |
|
|
|
|
|
|
|
|
Пусть ( Ω, F , P ) – произвольное вероятностное пространство, |
где |
Ω – |
||||||
пространство элементарных событий, |
F - σ -алгебра, P - вероятность. |
|
|
|||||
Числовая функция ξ = ξ (ω) от элементарного события |
ω Ω |
|
|
|
||||
|
ξ : Ω → R1 |
|
|
|
|
|
|
|
называется случайной величиной, если для любого действительного числа |
|
|||||||
x R1 : |
|
|
|
|
|
|
|
|
(5.1) |
{ ξ (ω) < x } = { ω |
| ξ (ω) < x } F |
|
|
|
|
|
|
Смысл этого определения состоит в следующем. Поскольку не любое |
|
|||||||
подмножество |
Ω является событием |
и все события |
составляют |
σ - алгебру |
||||
подмножеств F, то естественно рассматривать такие функции |
ξ = |
ξ (ω) |
, для |
|||||
которых имеет смысл говорить о вероятностях попадания |
в достаточно простые |
|||||||
множества . Свойство (5.1) гарантирует , что при любом |
х |
{ ω |
| |
ξ (ω) < x } |
||||
есть событие и , следовательно , имеет смысл говорить о его вероятности.
Дискретные случайные величины
Случайную величину называют дискретной, если множество ее возможных значений конечно или счетно .
29

Примеры : число очков , выпавших при бросании игральной кости; число
бросаний монеты до первого появления «герба». |
|
Для задания случайной величины |
недостаточно знать все ее возможные |
значения , две случайные величины |
могут иметь одинаковые возможные |
значения , но принимать их с различными вероятностями ( случайные величины-
оценки на экзамене |
у сильных и слабых студентов имеют одинаковые |
возможные значения, но разные вероятности). Поэтому необходимо указать и |
|
возможные значения |
случайной величины, и вероятности, с которыми она может |
их принять. |
|
Законом распределения дискретной случайной величины называется правило, по которому каждому возможному значению случайной величины ставится в соответствие вероятность, с которой случайная величина может принять это
значение. |
|
|
|
|
|
|
|||
|
|
Закон распределения дискретной |
случайной величины |
может быть задан |
|||||
графически, |
аналитически и таблично. В последнем случае задается таблица, где |
||||||||
в одной строке записаны все возможные значения |
xi , а в другой |
||||||||
соответствующие им вероятности. |
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
ξ |
|
X1 |
|
X2 |
|
Xn |
|
|
|
|
|
|
|
|
|
|
|
|
|
p |
|
P1 |
|
P2 |
|
Pn |
|
|
|
|
|
|
|
|
|
|||
|
Так как в результате опыта случайная величина может принять одно и только |
||||||||
одно |
из возможных значений, то события, заключающееся в том, что ξ примет |
||||||||
значение х 1 |
,х2 ,…,хn попарно несовместны и в сумме образуют достоверное |
||||||||
событие. Отсюда следует, что вероятность суммы этих событий равна 1 и мы приходим к важному соотношению
p1 + p2 +…+ pn = 1
Пример Составим закон распределение вероятностей для числа гербов при одном бросании монеты В виде таблицы
|
|
ξ |
|
|
0 |
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
p |
|
|
0,5 |
|
|
|
0,5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Или аналитически |
|
|
Р(ξ=k) = |
(0,5)2 |
, k=0,1 |
||||||||||||
Пример. Бросание игральной кости |
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ξ |
1 |
|
|
2 |
|
3 |
|
|
4 |
|
|
5 |
|
|
6 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
р |
1/6 |
1/6 |
|
1/6 |
|
1/6 |
|
1/6 |
|
1/6 |
||||||
Пример Бросание двух монет |
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
ξ |
|
0 |
|
1 |
|
|
|
|
2 |
|
|
|
|
|
||
30

|
р |
1/4 |
|
½ |
|
|
¼ |
|
|
||
|
|
|
|
|
|
|
|
5.4. Функция распределения |
|||
|
Функция |
F (x ) = P { ω | ξ (ω) < x } = P ( ξ < x ) , |
|||||||||
определенная при всех х |
R1 называется функцией распределения случайной |
||||||||||
величины ξ |
|
|
|
|
|
|
|
||||
|
Пример. Однократное бросание монеты |
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ξ |
|
0 |
|
|
1 |
|
|
|
|
|
|
P |
|
1/2 |
|
|
1/2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
F(x) =
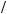

F(x)
1/2
0 |
1 |
x |
|
Пример Абитуриент сдает два вступительных экзамена по математике и физике. Составить закон распределения случайной величины ξ , числа полученных
пятерок , если вероятность |
получения пятерки по математике равна 0,8, а по |
|||||
физике – 0,6. Построить функцию распределения . |
||||||
Решение. |
Пусть А1 = {5 по математике} ; А2 = { 5 по физике} |
|||||
ξ =0 |
P( A1 A2 ) =P(A1 )P(A2 ) =0,2 0,4= 0,08 |
|||||
ξ =1 |
P ( A1 A2 + A1 A2 ) = 0,8 0,4 + 0,2 0,6 = 0,44 |
|||||
ξ = 2 |
P( A1 A2 ) = P(A1)P(A2 ) = 0,8 0,6 = 0,48 |
|||||
|
|
|
|
|
|
|
|
ξ |
0 |
1 |
|
2 |
|
|
p |
0,08 |
0,44 |
|
0,48 |
|
|
|
|
|
|
|
|
31
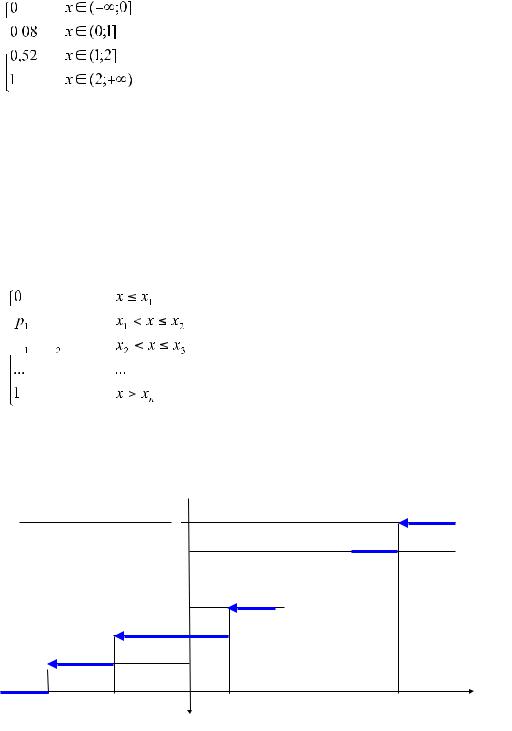
F(x) =

Если ξ дискретная конечная случайная величина
ξ |
X1 |
X2 |
… |
Xn |
p |
P1 |
P2 |
… |
Pn |
|
|
|
|
|
То в общем виде ее функция распределения строится следующим образом :
F(x) =
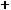

F(x)
1
P1+P2+…+Pn-1
P1+P2+P3
P1+P2
P1
x1 |
x2 |
0 |
x3 |
xn |
x |
|
Свойства функции распределения
1. |
0 ≤ F( x) ≤ 1 |
|
|
Доказательство. Так как F (x ) = P { ω | |
ξ (ω) < x } |
, а 0 ≤ P(А) ≤ 1 |
|
2. |
F(x) –является неубывающей функцией , т.е. для x1 |
< x2 F(x1 ) ≤ F (x2 ) |
|
Доказательство { ω | ξ (ω) < x1 } { ω |
| ξ (ω) < x2 } по свойству 3) |
||
вероятности |
|
|
|
P{ ω | ξ (ω) < x1 } ≤ P{ ω | ξ (ω) < x2 }
F(x1 ) ≤ F (x2 )
32

3. P { x1 ≤ ξ < x2 } = F (x2 ) – F (x1 )
Доказательство { ω | ξ (ω) < x2 } = { ω | ξ (ω) < x1 } {ω | x1 ≤ ξ (ω) < x2 }
по А3 определения вероятности
P{ ω | ξ (ω) < x2 } = P{ ω | ξ (ω) < x1 } + P{ω | x1 ≤ ξ (ω) < x2 } F (x2 ) = F (x1 ) + P{ω | x1 ≤ ξ (ω) < x2 }
4. F ( -∞ ) = 0 ; F (+ ∞) =1
Доказательство . Так как { ω | ξ (ω ) < - ∞ } = , { ω | ξ (ω ) < + ∞ } = Ω , то
P ( ) =0 , P (Ω ) =1 |
|
|
5. Функция распределения непрерывна слева , т.е. F(x)=F(x-0)= |
F(xn) |
|
Доказательство. x1 <x2 <…<xn <…<x |
xn =x |
|
Обозначим A={ ω |ξ(ω)<x} A1={ ω |ξ(ω)<x1}
A2={ ω | x 1≤ ξ(ω)<x2} , … An={ ω | x n-1≤ ξ(ω) < xn},…
A=A1 + A2 +…+ An+…
Где Ai Aj= при любых i ≠ j Тогда
P(A) =P(A1) + P(A2 )+…+P( An )+…= F(x1) + [ F(x2 )-F(x1) ]+ [ F(x3 )-F(x2) ]+…+= F(xn)
Но с другой стороны P(A) =F(x) следовательно F(x)=F(x-0)
33
