09-01-2015_09-46-11 / Лекция 9. ТВ и МС
.pdf
Лекция 9
Многомерные случайные величины и их законы распределения. Независимость случайных величин.
Совместное распределение случайных величин
Пусть даны две дискретные (конечные) случайные величины ξ и η .
ξ |
X1 |
X2 |
|
Xm |
p |
P1 |
P2 |
|
Pm |
|
|
|
|
|
|
|
|
|
|
η |
Y1 |
Y2 |
|
Yn |
|
|
|
|
|
p |
.q1 |
.q2 |
|
.qn |
|
|
|
|
|
Событие { ξ =xi , |
η = yj } |
состоит в том, что одновременно случайная |
величина ξ принимает значение |
xi , а случайная величина η - значение yj . |
|
Вероятности таких событий называются совместными вероятностями |
||
pij =P(ξ =xi , η = yj) |
, i=1,2,…,m , j=1,2,…,n |
|
Набор точек (xi , yj ) вместе с совместными вероятностями pij образуют совместное распределение случайных величин ξ и η .
Совместное распределение двух конечных случайных величин удобно задавать с помощью матрицы из m строк и n столбцов.
ξ \ η |
.y1 |
y2 … |
yj… |
yn |
|
X1 |
p11 |
p12 |
p1j |
p1n |
P1 |
X2 |
p21 |
p22 |
p2j |
p2n |
P2 |
. |
|
|
|
|
|
. |
|
|
|
|
|
x i |
Pi1 |
pi2 |
pij |
pin |
Pi |
xm |
Pm1 |
pm2 |
pmj |
pmn |
Pm |
|
q1 |
q2 |
qj |
qn |
1 |
|
|
|
|
|
|
Утверждение . Сумма всех совместных вероятностей равна единице
=1
Доказательство. Зафиксируем i и рассмотрим сумму : pi1 +pi2 +…+pin Вероятности произведения можно выразить через условные вероятности : P(AB)=P(A)P(B|A)
P(ξ =xi , η = yj)= P(ξ =xi )P( η = yj |(ξ =xi )
pi1 +pi2 +…+pin =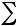 
P(ξ =xi )P( η = yj |(ξ =xi ) = P(ξ =xi )=pi
29
|
= p1 + p2 +…+ pm = 1 |
|
Аналогично, |
|
|
p1j +p2j |
+…+pmj = qj |
pij= q1 + q2 +…+ qn = 1 |
|
В матрице сумма чисел по строкам равна вероятности pi , а сумма по |
|
столбцам равна вероятностям qj . Таким образом , зная совместное распределение конечных случайных величин ξ и η можно восстановить законы распределения величин ξ и η . Обратное не верно (т.к. нужна дополнительная информация ).
В таблице вероятности pi и qj записываются как бы на «полях». Поэтому распределение случайных величин ξ и η называются маргинальными
( margin - поле) по отношению к их совместному распределению.
Пример. Пусть в урне по одному белому и черному шару. Из урны 2 раза наугад вынимают один шар и возвращают обратно. ξ – количество белых шаров в
1 раз , η |
- количество белых шаров во 2 раз . |
|||||||
|
|
|
|
|
|
|
|
|
|
|
ξ |
0 |
|
1 |
|
|
|
|
|
p |
0,5 |
|
0,5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
η |
0 |
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
p |
0,5 |
|
0,5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ξ\ η |
0 |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
1/4 |
1/4 |
|
½ |
|
|
|
1 |
|
1/4 |
1/4 |
|
½ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1/2 |
1/2 |
|
1 |
|
|
|
|
|
|
|
|
|
|
|
Пример. Пусть в урне по одному белому и черному шару. Из урны вынимаем один шар. ξ – количество вынутых белых шаров , η- количество оставшихся
белых шаров |
|
|
|
|||
|
|
ξ |
0 |
|
1 |
|
|
|
|
|
|
|
|
|
|
p |
0,5 |
|
0,5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
η |
0 |
|
1 |
|
|
|
|
|
|
|
|
|
|
p |
0,5 |
|
0,5 |
|
|
|
|
|
|
|
|
|
ξ\ η |
0 |
1 |
|
|
|
|
0 |
|
0 |
1/2 |
½ |
|
|
|
|
|
|
|
|
1 |
|
1/2 |
0 |
|
½ |
|
30
|
1/2 |
1/2 |
1 |
Случайные величины ξ и η называются независимыми, если независимы события { ξ =xi } и { η = yj } при любых i, j
Если случайные величины независимы, то по известным распределениям величин очень просто построить совместное распределение
pij = pi qj
Если же случайные величины зависимы, для того чтобы построить совместное распределение, требуется дополнительная информация .
5.2.2. Математические операции над случайными величинами
Произведением kξ случайной величины ξ на постоянную k называется случайная величина , которая принимает значения kxi с теми же вероятностями pi
kξ |
kX1 |
kX2 |
|
kXm |
p |
P1 |
P2 |
|
Pm |
|
|
|
|
|
|
|
|
|
|
ξ +c |
X1 +c |
X2 +c |
|
Xm +c |
|
|
|
|
|
p |
P1 |
P2 |
|
Pm |
k–й степенью случайной величины ξ , т.е. называется случайная величина , которая принимает значения xik с теми же вероятностями pi
ξk |
X1k |
X2k |
|
Xmk |
p |
P1 |
P2 |
|
Pm |
|
|
|
|
|
Пример Задан закон распределения случайной величины
ξ |
-2 |
1 |
2 |
р |
0,5 |
0,3 |
0,2 |
Найти закон распределения случайных величин 3ξ и ξ2
3ξ |
-6 |
3 |
6 |
р |
0,5 |
0,3 |
0,2 |
|
|
|
|
|
|
|
|
ξ2 |
4 |
1 |
4 |
р |
0,5 |
0,3 |
0,2 |
|
|
|
|
или
31
ξ2 |
|
1 |
4 |
|
|
р |
|
0,3 |
0,7 |
|
|
|
Суммой ( разностью или произведением) случайных величин |
ξ и η |
|||
называется случайная величина . которая принимает все возможные значения вида
xi + yj |
(xi - yj |
или |
xi yj ) |
с вероятностями pij |
|||||
|
Если случайные величины |
ξ и η независимы, то pij = pi qj |
|||||||
|
Пример. Даны законы распределения двух независимых случайных величин |
||||||||
|
|
|
|
|
|
|
|
|
|
|
ξ |
|
0 |
|
2 |
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
р |
|
0,5 |
|
0,2 |
|
0,3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
η |
|
-2 |
|
0 |
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
р |
|
0,1 |
|
0,6 |
|
0,3 |
|
|
Найти закон распределения случайной величины ξ - η . Если рассматривать ξ как выручку, η - затраты, то их разность ξ - η это прибыль.
32