
09-01-2015_09-46-11 / Лекция 4. ТВ и МС
.pdfЛекция 4 Определение условной вероятности. Теорема умножения вероятностей.
Независимость двух и нескольких событий..
4.1.Определение условной вероятности
Внекоторых случаях необходимо определить вероятность случайного события
А при условии, что произошло случайное событие |
В, имеющее ненулевую |
вероятность. То, что событие В произошло , сужает пространство элементарных |
|
событий до множества В, соответствующего этому событию. Т.е. мы находим
вероятность не на всем пространстве |
Ω |
, а на некотором его подмножестве Ω’. |
||
Так как подмножества пространства |
Ω задаются некоторыми дополнительными |
|||
условиями, то вероятности, связанные с |
принадлежащими этим подмножествам |
|||
событиями называются условными вероятностями. |
||||
Пример. Бросание игральной кости . Если мы находимся в условиях |
||||
симметричной классической схемы, |
|
|
||
Ω = {ω1 , ω2 ,ω3 ,ω4 ,ω5 , ω6 } , |
ωk = { выпало k очков } , k=1,2,..,6 |
|||
то вероятность события А ={Выпала 2 } и С={ выпала 3 } равна |
||||
|
|
Р(А) =Р (С)=1/6. |
||
Если нам сообщили, что выпала четное число, то общее число возможных |
||||
исходов |
уменьшилось до трех и следовательно шансы выпадения двойки |
|||
возрастают, а шансы выпадения тройки уменьшаются. |
||||
Ω ′ = { ω2 , ω4 , ω6 } , Р (А) =1/3. |
|
|
||
N(Ω)= 6 , |
m(A)=1 , m(С)=1 |
P(A)=1/6, P(С)=1/6 |
||
N(Ω’ )=3 |
, m(A)=1 , m(С)=0 |
|
P(A)=1/3 , P(С)=0 |
|
Если имеется дополнительная информация о том, что выпало четное число, то вероятность события А= {Выпала 2 }– возрастает с 1/6 до 1/3 , а вероятность события С={ выпала 3 } - уменьшилась с 1/6 до 0 .
Пусть дополнительная информация формулируется так : “Известно, что в результате эксперимента произошло событие В”. Зная это, мы хотим подсчитать
вероятность некоторого события |
А. Такую вероятность |
( при условии, что |
||||
произошло событие |
В) называют условной вероятностью события |
А и |
||||
обозначают Р( А | В). |
В предыдущем примере В= « выпало четное число» , |
|||||
А= « выпала 2», |
С= «выпала 3», |
то Р(А| В)= 1/3, |
Р(С | В)=0 |
|
||
Рассмотрим |
общую ситуацию в классической схеме. |
Пусть случайный |
||||
эксперимент имеет |
n равновозможных исходов. Допустим, известно, что |
|||||
произошло событие В. Какова условная вероятность события А ? |
|
|||||
Ясно, что общее число исходов уменьшается до тех , которые |
|
|||||
благоприятствуют событию В ( раз оно точно произошло, никаких других исходов произойти не могло). Это число обозначим через N(B) . Какие же исходы в данном случае будут благоприятными для события А ? Конечно, те, которые благоприятствуют одновременно событиям А и В, т.е. благоприятные для их произведения. Их количество равно N(AB).
23
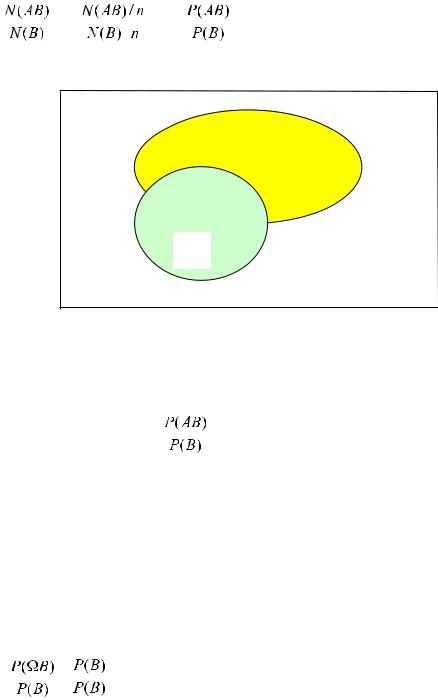
Если |
В произошло, то реализован один из N(В) исходов и событие А может |
||||||
произойти, только если произойдет один из исходов, благоприятствующих |
АВ, |
||||||
таких исходов N(AB) : |
N(Ω’)=N(B) , N(AB) |
|
|||||
Ω = {ω1 , ω2 , …,ωn } |
|
||||||
P(A|B)= |
|
= |
|
= |
|
|
|
|
|
|
|
|
|||
Ω
Ω1=B
A
Условной вероятностью события A при условии, что событие B с ненулевой вероятностью произошло, называется
(4.1) |
P(A|B)= |
|
, |
P(B) ≠ 0 |
|
||||
Теорема. |
Условная вероятность Р(А| В ) обладает всеми свойствами |
|||
безусловной вероятности Р(А) |
|
|
||
Доказательство. Для доказательства достаточно показать, что условная |
||||
вероятность удовлетворяет аксиомам А1, А2, А3 . |
||||
Р(А| В ) ≥ 0 |
, так как по определению условной вероятности числитель дроби |
|||
Р(АВ) является неотрицательным числом, а знаменатель Р(В) – положительным числом.
Так как ΩB=В , то выполняется аксиома А2 :
P(Ω |B)= |
|
|
= |
|
=1 |
|
|
|
|
|
|||
Если события А1 и А2 несовместны, то |
|
|||||
|
|
|
|
|
P(A1 + A2 |B)=P(A1 |B)+ P(A2 |B) |
|
Действительно, используя дистрибутивный закон, получаем |
||||||
|
|
|
|
( А1 + А2 )В = А1 В + А2 В |
|
|
Так как А1 |
и А2 несовместные , т.е. А1 А2 = |
,то (А1 В ) ( А2 В ) = и |
||||
события А1 В и А2 В так же несовместны , |
следовательно |
|||||
Р(( А1 + А2 ) В)= Р( А1 В + А2 В )= Р( А1 В ) + Р ( А2 В ) Откуда по определению
24

P(A1 + A2 |B) =  =
=  +
+  = P(A1 |B)+ P(A2 |B)
= P(A1 |B)+ P(A2 |B)
Следовательно, условная вероятность удовлетворяет аксиоме А3 вероятности.
Отметим некоторые свойства условной вероятности:
1. Р (А |А)=1 2. Если В А, то Р(А| В ) =1
3. Для любого события В с ненулевой вероятностью Р( | В)=0
Смысл доказанной теоремы заключается в том, что условная вероятность представляет собой безусловную вероятность , заданную на новом пространстве Ω′ элементарных событий , совпадающем с событием В.
|
Теорема умножения |
|
Переписывая (4.1) в форме |
2) |
P(AB)=P(A)P(B|A) |
получим равенство, которое называется теоремой умножения. Если исходить из определения (4.1), то содержательность теоремы умножения (4.2) представляется весьма невысокой. Однако при решении реальных задач можно найти условные вероятности исходя из некоторых дополнительных практических соображений, не прибегая к определению.
|
Теорема умножения может быть обобщена на любое число множителей : |
3) |
Р(А1 А2 …Аn )=Р(А1 )Р(А2 |A1 )P(A3 |A1 A2)…P(An | A1 A2 …An-1 ) |
Доказательство. Пусть имеются события А1 , А2 , …,Аn По определению условной вероятности имеем равенство,
P(An | A1 A2 …An-1 ) =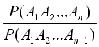
которое можно записать в виде
Р(А1 А2 …Аn )=Р( A1 A2 …An-1 ) P(An | A1 A2 …An-1 )
Аналогично находим
Р(А1 А2 …Аn-1 )=Р( A1 A2 …An-2 ) P(An-1 | A1 A2 …An-2 )
Тогда
Р(А1 А2 …Аn )= Р( A1 A2 …An-2 ) P(An-1 | A1 A2 …An-2 ) P(An | A1 A2 …An-1 )
Продолжая эту процедуру, получаем теорему умножения.
Пример . Пусть в урне находятся 4 белых и 6 черных шаров. Из урны наугад вынимают 2 шара , не возвращая их обратно. Какова вероятность того, что первый из выбранных шаров белый, а второй черный ?
Решение I ( по классической схеме)
N(Ω)=A102 =9 10=90, m(A)=4 6=24 P(A)=24/90=4/15
Решение II ( по теореме умножения)
А= {первым вынули белый шар} = {(б, )} В= {вторым вынули черный шар} = {( , ч)}
25

P(AB)=P(A)P(B|A)= |
|
|
|
=2/5 2/3=4/15 , P(A)=4/10 |
, P(B|A)=6/9 |
|
|
|
|||||
|
|
|
|
4.2. Независимые события |
|
|
Понятие независимости относится к одному из основных понятий в теории |
||||||
вероятностей. Рассмотрим пример с монетой: |
при многократном подбрасывании |
|||||
монеты результаты |
|
|
каждого эксперимента |
не зависят от результатов |
||
предыдущих опытов. Такие события естественно назвать независимыми.
Математически |
независимость означает, что условная вероятность некоторого |
события совпадает с его вероятностью (безусловной вероятностью). |
|
Говорят, что событие В не зависит от события А, если |
|
(4.4) |
P(B|A)=P(B) |
|
Свойства независимых событий |
♦ Если событие В не зависит от события А, то и событие А не зависит от В.
Доказательство. P(A|B)= =
=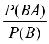 =
=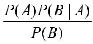 =
= =P(B)
=P(B)
События А и В называются независимыми , если выполняется равенство (4.4).
♦Если события А и В независимы, то
(4.5) P(AB) = P(A)P(B)
Доказательство. По теореме умножения получим
P(AB)=P(A)P(B|A)=P(A)P(B)
Равенство (4.5) используют часто в качестве определения независимых событий. События А и В называются независимыми, если вероятность произведения
событий равна произведению вероятностей этих событий
Р(АВ)=Р(А)Р(В).
Если события А и В независимы , то независимыми являются так же пары событий А и В, А и В , А и В .
В частности
Р(А |В)=1- Р(А |В)=1- Р(А) = Р(А)
Пример . В предыдущем примере изменим условие : вынув шар, кладем его обратно, и только затем вынимаем следующий.
Решение. Р(А)=4/10 , Р(В)=6/10 , P(A|B)=4/10 P(AB)=4/10 6/10=2/5 3/5=6/25
P(A|B)=P(A) P(B|A)=P(B)
Пример . Шифр сейфа состоит из 7-ми цифр. Чему равна вероятность набрать его с первого раза ?
Решение. Р(А)= (1/10)7
Следует различать по парную независимость и независимость в совокупности. События А1 , А2 , …,Аn называются независимыми в совокупности , если независимы между собой любые k ( k≤n ) из этих событий.
Например, если n=3 , то должны выполняться равенства |
|
||
Р(А1 |
А2 |
А3 )=Р(А1 )Р(А2)P(A3 ) |
26 |
|
|
|
|
Р(Аi |
Аj)=Р(Аi )Р(Аj) i,j=1,2,3 i≠ j |
Если события А1 , А2 |
, …,Аn независимы в совокупности, то имеет место |
равенство |
|
Р(А1 А2 …Аn )=Р(А1 )Р(А2)…P(An ) |
|
Пример С.Н. Бернштейна. Три грани правильного тетраэдра раскрашены в синий, красный и зеленый цвета, а в раскраске четвертой грани присутствуют все эти цвета.
А= {тетраэдр упал на грань в раскраске, которой присутствует синий цвет} В= { тетраэдр упал на грань в раскраске, которой присутствует красный цвет} С={ тетраэдр упал на грань в раскраске, которой присутствует зеленый цвет} Тогда
Р(А)=Р(В)=Р(С)=1/2 Р(АВ)=Р(ВС)=Р(АС)=1/4
Следовательно, события А,В,С попарно независимы Р(АВС)=1/4 ≠ Р(А)Р(В)Р(С)=1/8
Таким образом хотя события А,В,С попарно независимы, они зависимы в совокупности.
27
