09-01-2015_09-46-11 / Лекция 11. ТВ и МС

Лекция 11 Предельные теоремы теории вероятностей. Неравенство Чебышева. Закон

больших чисел в форме Чебышева Центральная предельная теорема

Неравенство Чебышева П.Л.

( позволяет оценить вероятность отклонения случайной величины от ее математического ожидания)

Теорема. Для каждой случайной величины ξ , имеющей дисперсию Dξ = σ2 ,

Пусть математического ожидание случайной величины равно a : Mξ = a ,

тогда дисперсия находится по формуле :

Dξ = (x1 – a)2 p1 + ( x2 – a )2 p2 + …+ (xn – a )2 pn

Вычислим вероятность события | ξ - a | ≥ ε , где ε > 0 .

Пусть xk1 , xk2 , …,xkm - те значения ξ , для которых имеет место

| xki – a | ≥ ε , i= 1,2,…,m .

Тогда

Dξ ≥ (xk1 – a)2 pk1 + ( xk2 – a )2 pk2 + …+ (xkm – a )2 pkm ≥ ε2 pk1 + ε2 pk2 + …+ ε2 pkm = ε2 ( pk1 + pk2 + …+ pkm ) = ε2 P{ | ξ - a | ≥ ε }

т.е. Dξ ≥ ε2 P{ | ξ - a | ≥ ε }

откуда и вытекает неравенство Чебышева (1).

Аналогично неравенство Чебышева доказывается и для непрерывного случая, при этом сумму нужно заменить на интеграл.

57

математического ожидания и дисперсии получим : Mη = M ( )=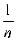

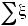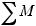
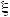
Dη = 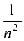D ( ) = D( ) =

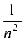
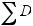
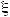
Применяя к случайной величине η следствие 1 , получаем :

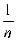
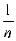
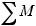
P{ | - 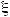| < ε } = P{ | η - Mη | < ε } ≥ 1 - 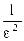Dη = 1-

6.2. Закон больших чисел

Последовательность случайных величин ξ1 , ξ2 ,…,ξn называется сходящейся по вероятности к числу b , если при n →∞ для ε > 0 :

Доказательство . Так как Dξi ≤ C , то ≤ C

Воспользовавшись следствием 2 неравенства Чебышева , получаем

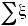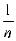
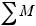
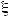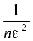
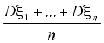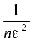P{ | - | < ε } ≥ 1 - ≥ 1 - C

Так как вероятность любого события не превышает 1, то

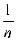
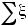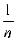
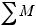
1 - C ≤ P{ | - 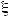| < ε } ≤ 1

Переходя в полученном неравенстве к пределу при n → ∞ , получаем утверждение теоремы.

Теорема 2. (ЗБЧ для одинаково распределенных случайных величин с конечной дисперсией ) Если последовательность ξ1 , ξ2 ,…,ξn,… независимых одинаково распределенных случайных величин такова, что M ξi = a , Dξi = σ2 , i=1,2,… то для ε > 0

58

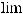P{ | 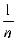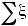- a | < ε } = 1

Доказательство. Так как 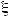= 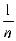na = a

дисперсии Dξi = σ2 , i следовательно они ограничены.

Тогда по теореме 1 (ЗБЧ в форме Чебышева ) получаем утверждение теоремы.

Теорема Бернулли ( ЗБЧ для числа успехов в испытании Бернулли)

случайных величин ) выполняется теорема Бернулли

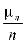-относительная частота успеха в n испытаниях Бернулли

6.4. Центральная предельная теорема

Пусть случайные величины ξ1 , ξ2 ,…,ξn,… - независимы , одинаково распределены с математическим ожиданием Mξi = a и конечной дисперсией

Dξi = σ2 . Тогда справедливо предельное соотношение

(1) P{ < x } = Ф(х) =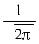 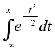- функция стандартного

! Соотношение можно переписать по –другому: при больших n : ( 1’ ) P(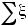 < x ) ≈ Ф ( )

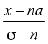В правой части равенства стоит не что иное , как функция распределения нормальной случайной величины .

факторов. В силу ЦПТ их суммарное воздействие можно приближенно описать с помощью нормального распределения.

59