23. Магнітна індукція соленоїда та тороїда.

Закон повного струму можна використати для розрахунку магніт­них полів тороїда і довгого соленоїда.

Тороїдом називають кільцеву ко­тушку, витки якої намотано на осердя, що має форму тора (мал. 171а). Лінії магнітної індукції поля тороїда повинні мати форму кіл, центри яких лежать на прямій, що проходить через центр тороїда і перпенди­кулярна до площини рисунка.

Циркуляція вектора 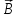вздовж кола радіусомдорівнює (мал. 171б):

Позначимо кількість витків обмотки тороїда N, а струм у ній -. Якщо, то коло радіусомне охоплює провідник зі струмом, томуі за законом повного струму, тобтоВ = 0.

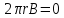Якщо то коло радіусомохоплює2N провідників зі струмомI. В N з них струм іде в одному напрямку, а в інших N провідниках - у зворотному. Тому алгебраїчна сума струмів у всіх провідниках дорівнює нулю. Й із закону пов­ного струмуі.

Отже, поза тороїдом магнітного по­ля нема. Воно цілком локалізується всере­дині об'єму тороїда Коло ра­діусомr, яке лежить всередині тороїда, охоплюєNпровідників, струми в яких до­рівнюютьIі однаково напрямлені. Тому

Отже,і

Індукція магнітного поля всередині тороїда зменшується зі збільшенням відс­тані від його центра:

де d - діаметр тора.

Індукція на основній лінії тороїда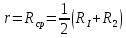дорівнює

де п - кількість витків на одиницю довжи­ни середньої лінії тороїда.

Розглянемо магнітну індукцію поля всередині соленоїда (мал. 172)- циліндри­чної котушки, яка складається з великої кількості витків, рівномірно намотаних на загальне осердя. Розглянемо соленоїд за­вдовжкиl, що маєNвитків, по якому тече струм.

Циркуляція вектора вздовж кон­туру у вигляді прямокутникаABCD, в якому сторонаBCдуже віддалена від солено­їда і який охоплює всіN витків соленоїда,

дорівнює

Інтеграл вздовж контуру ABCDAмо­жна подати у вигляді чотирьох інтегралів:

Магнітне поле соленоїда практично локалізовано в його об'ємі і на великій відстані від соленоїда магнітна індукція по­ля дорівнюватиме нулю:

А також

тому що . Тоді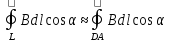

Вектори магнітної індукції в усіх точках всередині довгого соленоїда одна­кові, тобто числово рівні і мають однакові напрямки. Таке магнітне поле називається однорідним. Крім того, напрямок вектора індукції та переміщення збігаються, тому.

Отже,В результаті магнітна індукція поля всередині соленоїда у вакуумі дорівнює:деп - число витків на одиницю довжини соленоїда.

24.Потік вектора магнітної індукції.

Потоком вектора магнітної індукції (магнітним потоком) через площадку dS називається скалярна фізична величина, яка дорівнює добутку проекції векторана напрямок нормалідо площадкиdS і величини цієї площадки:

, де - проекція векторана напрямок нормалі до площадкиdS(- кут між векторамиі) (рис. 180),– вектор, модуль якого дорівнюєdS, а напрямок збігається з нормаллюдо площадкиdS.

Потік вектораможе бути як позитивним, так і негативним залежно від знакуcos(визначається вибором пози­тивного напрямку нормалі).

Потік вектора магнітної індукціїчерездовільнуповерхнюSдорівнює.Для однорідного поля і плоскої поверхні, розміщеної перпендикулярно до вектора,і.