55. Перетворення Лоренца

Перетворення Лоренца це лінійні перетворення координат, що залишають незмінним просторово-часовий інтервал. Перетворення Лоренца зв’язують координати подій в різних інерціальних системах відліку та мають фундаментальне значення в фізиці. Інваріантність фізичної теорії відносно перетворень Лоренца, або релятивістська інваріантність, є необхідною умовою достовірності цієї теорії. Перетворення Лоренца в системах з паралельними осями Найбільш розповсюджена форма запису перетворень Лоренца зв’язує координати події в інерціальній системі відліку K з координатами тієї ж в події в системі K′, яка рухається відносно K зі швидкістю V вздовж осі x: х’,y’ =y,z’ =zt’ = t – (V/c² )x / , де x, y, z, t – координати події в системі K; x′, y′, z′, t′ – координати тієї ж події в системі K′; V – відносна швидкість двох систем; c – швидкість світла. Зворотні формули (перехід від системи K′ до K) можна отримати заміною V → -V:x=x’+Vt’/,y’ =y,z’ =zt = t’ + (V/c² )x’ / Матричний запис перетворень Лоренца Часто, особливо в англомовній літературі, перетворення Лоренца записують у вигляді матриці повороту ||Λα′β||, що переводить компоненти 4-вектору xβ системи K в компоненти 4-вектору xα′ = Λα′βxβ, системи K′:

Формули перетворень Лоренца з довільною орієнтацією осей систем У випадку коли осі x координатних систем не паралельні швидкості формули перетворення були отримані Герглотцем у 1911 році. Для виводу цих формул зручно розділити радіус-вектор частки r в системі K на компоненту r||, яка паралельна швидкості V відносного руху інерціальних систем, та компоненту r⊥, яка перпендикулярна V. Тоді при переході до іншої системи K′ буде змінюватись тільки паралельна складова r||:

Остаточно для радіус-вектора частки в системі K′ r′ = r′|| + r′⊥формули будуть виглядати так:

Гіперболічна форма запису З математичної точки зору інтервал між двома подіями можна розглядати як "відстань" між двома точками в чотиривимірній системі координат. Отже, згідно визначення, перетворення Лоренца повинні зберігати незмінною будь-яку довжину в чотиривимірному просторі x, y, z, ct. Лінійними перетвореннями з такими властивостями є лише паралельні переноси та обертання системи координат. Паралельні переноси та обертання в площинах xy, yz, zx зводяться до переносу початку відліку простору та часу та звичайним просторовим поворотам. Останні три повороти системи координат в площинах tx, ty, tz і є перетвореннями Лоренца. Якщо ввести "кут повороту" ψ, такий що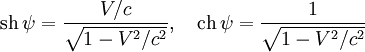то перетворення Лоренца для систем K та K′ з паралельними осями можна записати в гіперболічній формі:

ct′ = -x shψ + ct chψ,x′ = x chψ - ct shψ,y′ = y,z′ = z.

Ці формули відрізняються від звичайних формул перетворення при поворотах системи координат заміною тригонометричних функцій гіперболічними. В цьому виявляються відміни псевдоевклідової геометрії Мінковського від звичайної евклідової. Властивості перетворень Лоренца З формул перетворень легко побачити, що при граничному переході c→∞ до класичної механіки або — що те ж саме — при швидкостях значно менших швидкості світла формули перетворення Лоренца переходять в перетворення Галілея за принципом відповідності. При V > c координати x, t стають уявними, що означає той факт, що рух зі швидкістю, більшою за швидкість світла в вакуумі, неможливий. Неможливо навіть використовувати систему відліку, яка б рухалась зі швидкістю світла, бо тоді знаменники у формулах дорівнювали би нулю. На відміну від перетворень Галілея перетворення Лоренца некомутативні: результат двох послідовних перетворень Лоренца залежить від їх порядку. Математично це можна побачити з формального тлумачення перетворень Лоренца як обертань чотиривимірної системи координат, де, як відомо, результат двох обертань навколо різних осей залежить від порядку їх виконання. Виключенням з цього правила є лише перетворення з паралельними векторами швидкостей V1||V2, які еквівалентні поворотам системи координат відносно однієї осі.