
Geom / AnGeom_1
.pdf
Список литературы Векторная алгебра
Определение вектора
Системы координат на плоскости
Операции над векторами
Свойства сложения векторов
1) Ассоциативность. |
|
|
→− |
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
a |
|
|
c |
|
|
|
||||
|
Для любых векторов |
→− |
, |
|
b |
и |
|
|
|
|
||||||||
|
|
|
|
→− выполнено равенство |
||||||||||||||
|
( a + −→ |
−→ −→ |
−→ |
|
|
|
−→ |
. |
|
|
|
|||||||
|
−→ |
|
|
|
|
|
|
|
|
|
||||||||
|
|
b ) + c = a + ( b + c ) |
|
|
|
|
||||||||||||
2) Коммутативность. |
|
|
|
→− |
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
a |
|
|
|
|
|
|
|
|||
|
Для любых векторов →− |
|
и |
|
|
b |
выполнено |
|
|
|
||||||||
|
a + |
→− |
→− |
→− . |
|
|
|
|
|
|
|
|
|
|
|
|||
|
→− |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
b = b + a |
|
|
|
|
|
|
|
|
|
|
|
|||||
3) Нулевой вектор. |
|
|
|
|
|
|
|
|
→− |
|
|
|||||||
|
|
|
|
|
|
|
|
a |
|
|
|
|
|
|
a + |
|
|
|
|
Для любого вектора →− |
выполнено →− |
0 = a |
|||||||||||||||
|
|
→− . |
||||||||||||||||
4) Противоположный вектор. |
|
|
|
|
→− |
|
||||||||||||
|
|
|
|
|
|
|
|
a |
|
|
|
|
|
|
|
|
|
|
|
Для любого вектора |
→− |
существует вектор |
b |
такой, что |
|||||||||||||
|
a + |
→− |
→− |
|
|
|
|
→− |
|
|
|
|
|
|
|
|
|
|
|
→− |
b = 0 |
. Вектор |
b |
называется противоположным к |
|||||||||||||
|
|
|
|
|||||||||||||||
|
a |
|
|
|
|
|
a |
|
|
|
|
|
|
|
|
|
|
|
|
→− и обозначается −→− . |
|
|
|
|
|
|
|
|
|
|
|||||||
Аналитическая геометрия. Лекция 1

Список литературы Векторная алгебра
Определение вектора
Системы координат на плоскости
Операции над векторами
Свойства сложения векторов
1) Ассоциативность. |
|
|
→− |
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
a |
|
|
c |
|
|
|
||||
|
Для любых векторов |
→− |
, |
|
b |
и |
|
|
|
|
||||||||
|
|
|
|
→− выполнено равенство |
||||||||||||||
|
( a + −→ |
−→ −→ |
−→ |
|
|
|
−→ |
. |
|
|
|
|||||||
|
−→ |
|
|
|
|
|
|
|
|
|
||||||||
|
|
b ) + c = a + ( b + c ) |
|
|
|
|
||||||||||||
2) Коммутативность. |
|
|
|
→− |
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
a |
|
|
|
|
|
|
|
|||
|
Для любых векторов →− |
|
и |
|
|
b |
выполнено |
|
|
|
||||||||
|
a + |
→− |
→− |
→− . |
|
|
|
|
|
|
|
|
|
|
|
|||
|
→− |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
b = b + a |
|
|
|
|
|
|
|
|
|
|
|
|||||
3) Нулевой вектор. |
|
|
|
|
|
|
|
|
→− |
|
|
|||||||
|
|
|
|
|
|
|
|
a |
|
|
|
|
|
|
a + |
|
|
|
|
Для любого вектора →− |
выполнено →− |
0 = a |
|||||||||||||||
|
|
→− . |
||||||||||||||||
4) Противоположный вектор. |
|
|
|
|
→− |
|
||||||||||||
|
|
|
|
|
|
|
|
a |
|
|
|
|
|
|
|
|
|
|
|
Для любого вектора |
→− |
существует вектор |
b |
такой, что |
|||||||||||||
|
a + |
→− |
→− |
|
|
|
|
→− |
|
|
|
|
|
|
|
|
|
|
|
→− |
b = 0 |
. Вектор |
b |
называется противоположным к |
|||||||||||||
|
|
|
|
|||||||||||||||
|
a |
|
|
|
|
|
a |
|
|
|
|
|
|
|
|
|
|
|
|
→− и обозначается −→− . |
|
|
|
|
|
|
|
|
|
|
|||||||
Аналитическая геометрия. Лекция 1

Список литературы Векторная алгебра
Определение вектора
Системы координат на плоскости
Операции над векторами
Свойства сложения векторов
1) Ассоциативность. |
|
|
→− |
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
a |
|
|
c |
|
|
|
||||
|
Для любых векторов |
→− |
, |
|
b |
и |
|
|
|
|
||||||||
|
|
|
|
→− выполнено равенство |
||||||||||||||
|
( a + −→ |
−→ −→ |
−→ |
|
|
|
−→ |
. |
|
|
|
|||||||
|
−→ |
|
|
|
|
|
|
|
|
|
||||||||
|
|
b ) + c = a + ( b + c ) |
|
|
|
|
||||||||||||
2) Коммутативность. |
|
|
|
→− |
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
a |
|
|
|
|
|
|
|
|||
|
Для любых векторов →− |
|
и |
|
|
b |
выполнено |
|
|
|
||||||||
|
a + |
→− |
→− |
→− . |
|
|
|
|
|
|
|
|
|
|
|
|||
|
→− |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
b = b + a |
|
|
|
|
|
|
|
|
|
|
|
|||||
3) Нулевой вектор. |
|
|
|
|
|
|
|
|
→− |
|
|
|||||||
|
|
|
|
|
|
|
|
a |
|
|
|
|
|
|
a + |
|
|
|
|
Для любого вектора →− |
выполнено →− |
0 = a |
|||||||||||||||
|
|
→− . |
||||||||||||||||
4) Противоположный вектор. |
|
|
|
|
→− |
|
||||||||||||
|
|
|
|
|
|
|
|
a |
|
|
|
|
|
|
|
|
|
|
|
Для любого вектора |
→− |
существует вектор |
b |
такой, что |
|||||||||||||
|
a + |
→− |
→− |
|
|
|
|
→− |
|
|
|
|
|
|
|
|
|
|
|
→− |
b = 0 |
. Вектор |
b |
называется противоположным к |
|||||||||||||
|
|
|
|
|||||||||||||||
|
a |
|
|
|
|
|
a |
|
|
|
|
|
|
|
|
|
|
|
|
→− и обозначается −→− . |
|
|
|
|
|
|
|
|
|
|
|||||||
Аналитическая геометрия. Лекция 1
Список литературы Векторная алгебра
Определение вектора
Системы координат на плоскости
Операции над векторами
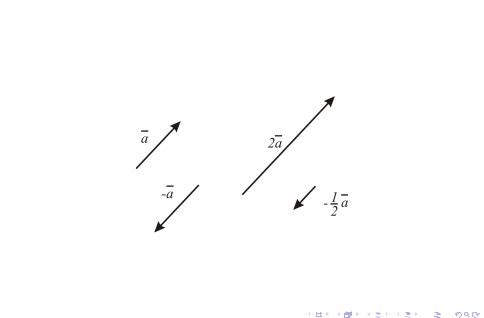
Умножение вектора на число
Аналитическая геометрия. Лекция 1

Список литературы Векторная алгебра
Определение вектора
Системы координат на плоскости
Операции над векторами
Свойства умножения вектора на число
1) λ→− |
||→− |
a |
a |
| →− | | ||→− |
2)λ a = λ a
3)Ассоциативность.
|
|
|
|
a |
и чисел |
α |
, |
β |
выполнено |
||||
|
Для любого вектора →− |
|
|
||||||||||
|
(αβ)→− |
→− |
. |
|
|
|
|
|
|
|
|
|
|
|
a = α(β a ) |
|
|
|
|
|
|
|
|
|
|
|
|
4) Дистрибутивность. |
|
|
|
|
|
, |
|
выполнено |
|||||
|
|
|
|
|
a |
|
|
|
α |
β |
|||
|
2.1) Для любого вектора →− и чисел |
|
|
||||||||||
|
(α + β)→− →− →− . |
|
|
|
|
|
|
|
|
|
|||
|
a = α a + β a |
|
a |
|
|
→− |
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
α |
|||
|
2.2) Для любых двух векторов →− |
|
и |
b |
|
и числа |
|||||||
|
|
α( a + |
→− |
|
→− |
|
|
|
|
|
|
||
|
выполнено |
→− |
|
b ) = α a + α b |
. |
|
|
|
|
|
|||
|
|
|
→− |
|
|
|
|
|
|
|
|||
Аналитическая геометрия. Лекция 1

Список литературы Векторная алгебра
Определение вектора
Системы координат на плоскости
Операции над векторами
Свойства умножения вектора на число
1) λ→− |
||→− |
a |
a |
| →− | | ||→− |
2)λ a = λ a
3)Ассоциативность.
|
|
|
|
a |
и чисел |
α |
, |
β |
выполнено |
||||
|
Для любого вектора →− |
|
|
||||||||||
|
(αβ)→− |
→− |
. |
|
|
|
|
|
|
|
|
|
|
|
a = α(β a ) |
|
|
|
|
|
|
|
|
|
|
|
|
4) Дистрибутивность. |
|
|
|
|
|
, |
|
выполнено |
|||||
|
|
|
|
|
a |
|
|
|
α |
β |
|||
|
2.1) Для любого вектора →− и чисел |
|
|
||||||||||
|
(α + β)→− →− →− . |
|
|
|
|
|
|
|
|
|
|||
|
a = α a + β a |
|
a |
|
|
→− |
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
α |
|||
|
2.2) Для любых двух векторов →− |
|
и |
b |
|
и числа |
|||||||
|
|
α( a + |
→− |
|
→− |
|
|
|
|
|
|
||
|
выполнено |
→− |
|
b ) = α a + α b |
. |
|
|
|
|
|
|||
|
|
|
→− |
|
|
|
|
|
|
|
|||
Аналитическая геометрия. Лекция 1

Список литературы Векторная алгебра
Определение вектора
Системы координат на плоскости
Операции над векторами
Свойства умножения вектора на число
1) λ→− |
||→− |
a |
a |
| →− | | ||→− |
2)λ a = λ a
3)Ассоциативность.
|
|
|
|
a |
и чисел |
α |
, |
β |
выполнено |
||||
|
Для любого вектора →− |
|
|
||||||||||
|
(αβ)→− |
→− |
. |
|
|
|
|
|
|
|
|
|
|
|
a = α(β a ) |
|
|
|
|
|
|
|
|
|
|
|
|
4) Дистрибутивность. |
|
|
|
|
|
, |
|
выполнено |
|||||
|
|
|
|
|
a |
|
|
|
α |
β |
|||
|
2.1) Для любого вектора →− и чисел |
|
|
||||||||||
|
(α + β)→− →− →− . |
|
|
|
|
|
|
|
|
|
|||
|
a = α a + β a |
|
a |
|
|
→− |
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
α |
|||
|
2.2) Для любых двух векторов →− |
|
и |
b |
|
и числа |
|||||||
|
|
α( a + |
→− |
|
→− |
|
|
|
|
|
|
||
|
выполнено |
→− |
|
b ) = α a + α b |
. |
|
|
|
|
|
|||
|
|
|
→− |
|
|
|
|
|
|
|
|||
Аналитическая геометрия. Лекция 1

Список литературы Векторная алгебра
Определение вектора
Системы координат на плоскости
Операции над векторами
Свойства умножения вектора на число
1) λ→− |
||→− |
a |
a |
| →− | | ||→− |
2)λ a = λ a
3)Ассоциативность.
|
|
|
|
a |
и чисел |
α |
, |
β |
выполнено |
||||
|
Для любого вектора →− |
|
|
||||||||||
|
(αβ)→− |
→− |
. |
|
|
|
|
|
|
|
|
|
|
|
a = α(β a ) |
|
|
|
|
|
|
|
|
|
|
|
|
4) Дистрибутивность. |
|
|
|
|
|
, |
|
выполнено |
|||||
|
|
|
|
|
a |
|
|
|
α |
β |
|||
|
2.1) Для любого вектора →− и чисел |
|
|
||||||||||
|
(α + β)→− →− →− . |
|
|
|
|
|
|
|
|
|
|||
|
a = α a + β a |
|
a |
|
|
→− |
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
α |
|||
|
2.2) Для любых двух векторов →− |
|
и |
b |
|
и числа |
|||||||
|
|
α( a + |
→− |
|
→− |
|
|
|
|
|
|
||
|
выполнено |
→− |
|
b ) = α a + α b |
. |
|
|
|
|
|
|||
|
|
|
→− |
|
|
|
|
|
|
|
|||
Аналитическая геометрия. Лекция 1

Список литературы Векторная алгебра
Определение вектора
Системы координат на плоскости
Операции над векторами
Теорема.
−→ −→
Векторы a и b являются коллинеарными тогда и только
тогда, когда один из векторов можно выразить через другой умножением на число.
Доказательство.
Необходимость. |
|
→− |
|
||
a |
→− |
|
a |
|
|
Пусть →− || |
b |
. Отложив |
b |
от одной точки, получим, что |
|
|
→− и |
|
|||
оба вектора |
лежат на одной прямой. Если один из векторов, |
||||||
a |
|
→− |
|
|
· |
→− |
|
например →− |
, равен |
0 |
a |
= 0 |
|
b |
. |
|
, то →− |
|
|
|
|||
Аналитическая геометрия. Лекция 1

Список литературы Векторная алгебра
Определение вектора
Системы координат на плоскости
Операции над векторами
Теорема.
−→ −→
Векторы a и b являются коллинеарными тогда и только
тогда, когда один из векторов можно выразить через другой умножением на число.
Доказательство.
Необходимость. |
|
→− |
|
||
a |
→− |
|
a |
|
|
Пусть →− || |
b |
. Отложив |
b |
от одной точки, получим, что |
|
|
→− и |
|
|||
оба вектора |
лежат на одной прямой. Если один из векторов, |
||||||
a |
|
→− |
|
|
· |
→− |
|
например →− |
, равен |
0 |
a |
= 0 |
|
b |
. |
|
, то →− |
|
|
|
|||
Аналитическая геометрия. Лекция 1
