
- •Глава 1. Функции нескольких переменных
- •1. Предварительные определения
- •2. Открытые и замкнутые множества
- •3. Предел функции нескольких переменных
- •4. Функции, непрерывные в точке
- •5. Функции, непрерывные на множестве
- •6. Частные производные
- •7. Производная сложной функции
- •8. Производные высших порядков
- •9. Оператор Лапласа
- •10. Неявные функции
- •11. Формула Тейлора для функций нескольких переменных
- •12. Экстремумы функций нескольких переменных
- •Глава 2. Функциональные последовательности и ряды
- •1. Поточечная и равномерная сходимость.
- •2. Функциональные ряды.
- •3. Признаки Абеля и Дирихле
- •4. Свойства равномерно сходящихся последовательностей и рядов.
- •5. Степенные ряды
- •6. Ряд Тейлора
- •Исторические сведения
- •Абель
- •Адамар
- •Д’Аламбер
- •Больцано
- •Вейерштрасс
- •Дирихле
- •Коши
- •Лаплас
- •Лейбниц
- •Ньютон
- •Сильвестр
- •Тейлор
ç |
|
è |
|
|
|
Глава 2. Функциональные последовательности и ряды
1. Поточечная и равномерная сходимость.
Пусть { fn}+∞n=1 — последовательность функций, определенных на некотором промежутке I . Говорят, что эта последовательность сходится в точке x0 I , если числовая последовательность { fn (x0 )}+∞n=1 является схо-
дящейся. Говорят, что последовательность { fn}+∞n=1 сходится на промежутке I поточечно, если она сходится в каждой точке x I . Полагая в
этом случае |
f (x) = lim fn (x) |
для каждого |
x I , получаем некоторую |
функцию f , |
n→+∞ |
|
|
определенную на промежутке I . В силу единственности пре- |
|||
дела сходящейся числовой последовательности, эта функция определяется исходной функциональной последовательностью единственным образом. Говорят, что данная функциональная последовательность поточечно сходится к функции f . Наличие такого соотношения записывается следую-
щим образом: fn (x) → f (x), x I .
Проанализируем данное определение. Для каждой точки x I по любому ε > 0 найдется такое N , что для всех n ≥ N выполняется неравенство | fn (x) − f (x) |<ε . Отметим, что число N зависит как от числа ε , так и
от выбранной точки x . Если для любого ε > 0 можно найти число N , обладающее указанными свойствами и не зависящее от x , говорят, что данная функциональная последовательность сходится к функции f равномер-
но на промежутке I . Приведем точное определение.
ОПРЕДЕЛЕНИЕ. Пусть { fn}+∞n=1 — последовательность функций, определенных на промежутке I , f — функция, определенная на этом проме-
жутке. Говорят, что указанная последовательность равномерно сходится на промежутке I к функции f , если по любому ε > 0 найдется такое N , что
для всех n ≥ N и всех x I выполняется неравенство | fn (x) − f (x) |<ε . Наличие такого соотношения записывается следующим образом:
I
fn (x) f (x) , x I или fn f .
ЗАМЕЧАНИЕ 1. Очевидно, что из равномерной сходимости на множестве I вытекает поточечная сходимость на этом множестве. Обратное утверждение, как мы увидим ниже на примерах, вообще говоря, неверно.
ЗАМЕЧАНИЕ 2. Условие равномерной сходимости на множестве I может быть записано следующим образом:
Глава 2 |
58 |
Функциональные ряды |
||
|
|
|
|
|
ç |
|
|
|
è |
|
|
|
|
|
lim sup | fn (x) − f (x) |= 0. |
( ) |
|
n→+∞ x I |
|
|
Действительно. Допустим, что fn (x) f (x) , |
x I . Выберем произвольное |
|
ε > 0 и найдем такое N , что для всех n ≥ N |
и всех x I |
выполняется не- |
равенство | fn (x) − f (x) |<ε . Отсюда следует, что
su p| fn (x) − f (x) |≤ε, n ≥ N.
x I
Полученное соотношение означает, что выполняется условие ( ). Аналогично из условия ( )выводится равномерная сходимость рассматриваемой последовательности.
ЗАМЕЧАНИЕ 3. Рассмотрим произвольную сходящуюся числовую последовательность {an}+∞n=1. Ее можно рассматривать как последовательность
функций, определенных на произвольном промежутке I и принимающих постоянные значения. Очевидно, что эта функциональная последовательность будет также сходится на этом промежутке, причем равномерно.
ЗАДАЧА. Дать прямое определение того, что последовательность { fn}+∞n=1 не сходится равномерно к функции f .
ЗАДАЧА. Сформулировать определения сходимости в точке, на промежутке и равномерной сходимости на промежутке, пользуясь языком кванторов.
Приведем некоторые примеры.
ПРИМЕР 1. Рассмотрим последовательность функций fn (x) = 1n sin(nx) , n =1, 2, …,
определенных на всей вещественной оси . Очевидно, что для любого вещественного x выполняется равенство nlim→+∞ fn (x) = 0 , то есть данная по-
следовательность поточечно сходится к нулевой функции. Покажем, что сходимость данной последовательности к нулевой функции является равномерной. Воспользуемся оценкой
| fn (x) |= |
|
1 sin nx |
|
≤ |
1 . |
|
|
||||
|
|
n |
|
|
n |
Выберем произвольное ε > 0. Из полученной оценки следует, что если
1 |
|
|
|
|
1 |
n <ε , то |
| fn (x) |<ε для всех x . Неравенство n <ε равносильно усло- |
||||
вию n > |
1 |
, или |
|
1 |
|
ε |
n ≥ N , где N = |
ε |
+1. Итак, мы доказали, что для любого |
||
|
|
|
|
||
ε > 0 найдется такое N = N(ε) , |
что для всех n ≥ N выполняется неравен- |
||||
ство | fn (x) |<ε , |
x . Поскольку число N можно взять не зависящим от |
||||
Глава 2 |
59 |
Функциональные ряды |
||
|
|
|
|
|
ç |
|
|
|
è |
|
|
|
|
|
точек x , это по определению и означает наличие равномерной сходимости к нулевой функции.
Можно провести анализ несколько в иной форме, воспользовавшись формулировкой из замечания 2. Равномерная сходимость следует из соотношений
|
sup |
|
sin nx |
−0 |
|
=sup |
|
sin nx |
|
= |
1 |
→0 |
|
|
|
|
|
|
|||||||||
|
|
|
n |
|
|
|
|
n |
|
|
n |
|
|
при n → +∞. |
x |
|
|
|
|
x |
|
|
|
|
|
|
|
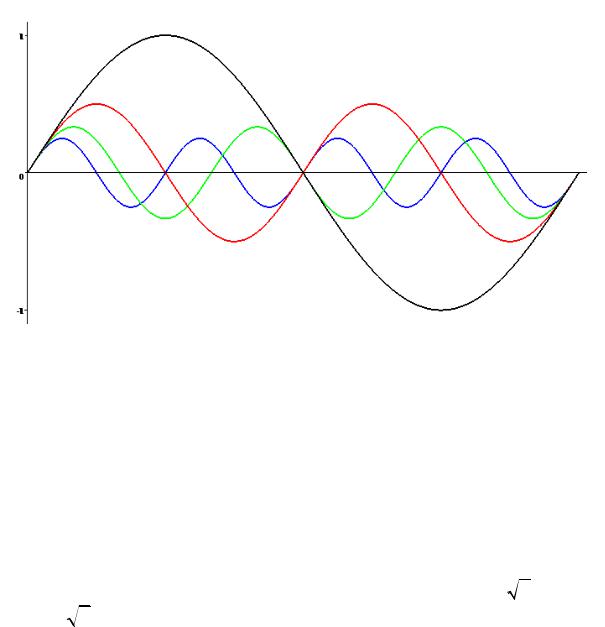
1 sin(nx) на промежутке [0,2π] при n =1, 2 , 3 и 4 изо- |
|||||||||||||
Графики функций |
|||||||||||||
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
бражены на следующем рисунке.
ПРИМЕР 2. Рассмотрим последовательность функций fn (x) = xn , x [0,1), n =1, 2,… .
Мы знаем, что lim xn = 0 для x [0,1), то есть данная последовательность
n→+∞
поточечно сходится на рассматриваемом промежутке к нулевой функции. Покажем, что эта сходимость не является равномерной. Обозначим через f функцию, определенную на промежутке [0,1) и тождественно рав-
ную нулю.
Выберем произвольное ε , удовлетворяющее условию 0 <ε <1, возьмем любое натуральное значение n и найдем, для каких значений x [0,1)
выполняется неравенство | fn (x) − f (x) |<ε . В данном случае последнее неравенство принимает вид xn <ε , что равносильно условию x < n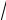 ε . Учитывая, что n
ε . Учитывая, что n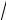 ε <1, получаем, что при любом значении n неравенство
ε <1, получаем, что при любом значении n неравенство
| fn (x) − f (x) |<ε

Глава 2 |
60 |
Функциональные ряды |
||
|
|
|
|
|
ç |
|
|
|
è |
|
|
|
|
|
выполняется не для всех x [0,1). Это означает, что сходимость данной последовательности функций к нулевой функции не является равномерной.
Отметим, что в данном случае su p| fn (x) − f (x) |=1 0 при n → +∞, |
||
0≤x<1 |
|
|
что также говорит об отсутствии равномерной сходимости. |
||
ПРИМЕР 3. Пусть fn (x) = xn − xn+1, 0 ≤ x ≤1, n . |
||
Очевидно, что при любом значении x [0,1] |
lim fn (x) = 0 . Пока- |
|
жем, что сходимость fn (x) →0, x [0,1] |
|
n→+∞ |
является не только поточечной, |
||
но и равномерной. Рассмотрим величину |
sup | fn (x) |, которая, в силу того, |
|
|
0≤x≤1 |
|
что функции fn принимают неотрицательные значения и непрерывны на
отрезке [0,1], совпадает с величиной max fn (x) . Найдем наибольшее зна-
0≤x≤1
чение функции fn на отрезке [0,1]. Функция fn дифференцируема на отрезке [0,1]. Поэтому свое наибольшее значение она принимает либо на од-
ном из концов отрезка, либо во внутренней стационарной точке, то есть в точке x , удовлетворяющей условию fn′(x) = 0 , 0 < x <1. Из соотношения
fn′(x) = nxn−1 −(n +1)xn
находим стационарную точку |
x = |
|
n |
|
. Учитывая, |
что |
|
|
f (0) = 0, f (1) = 0, |
|||||||||||||||
n +1 |
|
|
||||||||||||||||||||||
получаем, что |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
n |
|
|
|
|
|
|
n+1 |
|
||||
max fn (x) = f |
n |
|
|
|
|
|
n |
|
|
n |
|
|
|
|||||||||||
|
|
|
|
|
|
|
= |
|
|
|
|
− |
|
|
|
|
|
|
|
= |
||||
|
|
|
1 |
|
|
|
|
|
|
|
|
|
||||||||||||
0≤x≤1 |
|
n + |
|
n +1 |
|
n +1 |
|
|
|
|||||||||||||||
n |
n |
|
|
|
n |
|
|
|
|
|
n |
n |
1 |
|
|
|
|
|
1 |
|
||||
= |
|
|
1 |
− |
|
|
|
|
|
|
= |
|
|
|
|
|
|
|
< |
|
|
|
|
. |
|
|
|
|
|
|
|
|
|
n +1 |
n |
+1 |
|||||||||||||
n +1 |
|
|
|
n +1 |
n +1 |
|
|
|||||||||||||||||
Следовательно, lim sup | fn (x) |= 0 , и сходимость является равномерной.
n→+∞0≤x≤1
ПРИМЕР 4. Пусть fn (x) = xn − x2n , 0 ≤ x ≤1, n .
В этом случае f (x) = nlim→+∞ fn (x) = 0 для всех x [0,1]. Находим стационарные точки функции fn . Соотношение fn′(x) = 0 переписываем в ви-
де nxn−1 − 2nx2n−1 = 0 , откуда получаем, что единственной внутренней ста-
ционарной точкой является x = |
1 |
|
. Учитывая, что |
|
fn (0) = 0, fn (1) = 0 , на- |
|||||||
|
|
|
||||||||||
ходим: |
n 2 |
|
|
|
|
|
|
|
|
|||
|
|
|
|
1 |
|
|
|
1 |
|
|||
|
|
|
|
|
|
|
|
|||||
su p| fn (x) − f (x) |= max fn (x) = |
fn |
|
|
|
|
= |
4 |
0 |
||||
|
|
|
||||||||||
|
||||||||||||
0≤x≤1 |
0≤x≤1 |
n 2 |
|
|
|
|
||||||
Глава 2 |
61 |
Функциональные ряды |
||
|
|
|
|
|
ç |
|
|
|
è |
|
|
|
|
|
при n → +∞. Поэтому сходимость функций fn к нулевой функции равномерной не является.
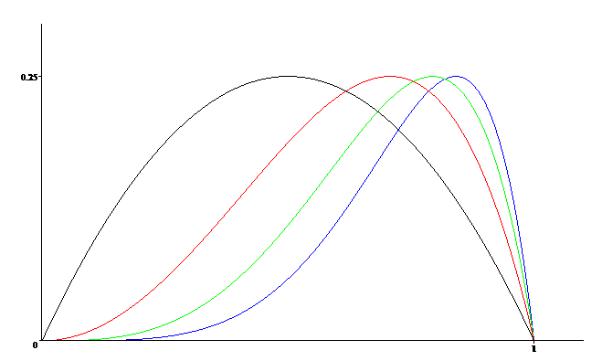
Графики функций xn − x2n при n =1, 2 , 3 и 4 изображены на следующем рисунке.
ЗАМЕЧАНИЕ. Можно доказать отсутствие равномерной сходимости в предыдущем примере по следующей схеме. Рассмотрим функцию
ϕ(x) = x − x2 , 0 ≤ x ≤1.
Из соотношения ϕ(x) = x(1− x) следует, что эта функция обращается в
ноль на концах отрезка и принимает положительные значения во всех его внутренних точках. При любом натуральном значении n отображение
x → xn взаимно-однозначно отображает отрезок [0,1] на себя. Поэтому
множество значений функции |
ϕ(xn ) , 0 ≤ x ≤1 |
совпадает с множеством |
значений функции ϕ(x), 0 ≤ x ≤1. Учитывая, что |
fn (x) =ϕ(xn ) , отсюда по- |
|
лучаем, что |
|
|
max fn (x) = maxϕ(x) = const > 0, |
||
0≤x≤1 |
0≤x≤1 |
|
что и говорит об отсутствии равномерной сходимости к нулю. Приведенная схема рассуждений может быть перенесена на случай последовательности функций
fn (x) = xαn − xβn , 0 ≤ x ≤1, n =1,2, ,
где α , β — постоянные, 0 <α < β . Здесь также будет иметь место поточечная, но не равномерная сходимость к нулевой функции.
Глава 2 |
62 |
Функциональные ряды |
||
|
|
|
|
|
ç |
|
|
|
è |
|
|
|
|
|
Отметим следующие простые свойства равномерно сходящихся последовательностей функций.
I
1) Равномерная сходимость fn f равносильная условию
I
fn − f 0 .
I I I
2) Если fn f , gn g , то fn ± gn f ± g .
I
3) Если fn f , g — произвольная функция, определенная на про-
I
межутке I , то fn + g f + g .
I
4) Если fn f , ϕ — ограниченная функция, определенная на про-
I
межутке I , то ϕ fn ϕ f .
Приведем теперь необходимое и достаточное условие равномерной сходимости функциональной последовательности.
ТЕОРЕМА 1 (КРИТЕРИЙ КОШИ РАВНОМЕРНОЙ СХОДИМОСТИ ФУНКЦИОНАЛЬНОЙ ПОСЛЕДОВАТЕЛЬНОСТИ). Пусть { fn}+∞n=1 — последовательность
функций, определенных на промежутке I . Эта последовательность является равномерно сходящейся на этом промежутке в том и только том случае, когда для любого числа ε > 0 найдется такое значение N , что для всех n ≥ N , p =1, 2 , … и всех x I выполняется неравенство
| fm (x) − fn (x) |<ε.
ДОКАЗАТЕЛЬСТВО. 1. Предположим, что последовательность { fn}+∞n=1 равномерно сходится на промежутке I к функции f . Выберем произвольное ε > 0 и найдем такое число N , что для всех n ≥ N и всех x I выпол-
няется неравенство | fn (x) − f (x) |< ε2 . Тогда для тех же значений n и всех p =1, 2 , … выполняется неравенство n + p > N и, следовательно, для про-
извольного |
x I имеем: | fn+p (x) − f (x) |< ε . Отсюда получаем, что для |
||
|
2 |
|
|
всех n ≥ N , |
p =1, 2 , … и произвольного x I |
|
|
|
| fn+p (x) − fn (x) |=| ( fn+p (x) − f (x)) −( fn (x) − f (x) |≤ |
||
|
≤| fn+p (x) − f (x) | +| fn (x) − f (x) |< |
ε |
+ ε =ε. |
|
|
2 |
2 |
2.Докажем обратное утверждение. Предположим, что для любого
ε> 0 найдется такое N , что для всех n ≥ N , p =1, 2 , … и произвольного
xI выполняется неравенство | fn+p (x) − fn (x) |<ε . Отсюда следует, что
