
- •Глава 1. Функции нескольких переменных
- •1. Предварительные определения
- •2. Открытые и замкнутые множества
- •3. Предел функции нескольких переменных
- •4. Функции, непрерывные в точке
- •5. Функции, непрерывные на множестве
- •6. Частные производные
- •7. Производная сложной функции
- •8. Производные высших порядков
- •9. Оператор Лапласа
- •10. Неявные функции
- •11. Формула Тейлора для функций нескольких переменных
- •12. Экстремумы функций нескольких переменных
- •Глава 2. Функциональные последовательности и ряды
- •1. Поточечная и равномерная сходимость.
- •2. Функциональные ряды.
- •3. Признаки Абеля и Дирихле
- •4. Свойства равномерно сходящихся последовательностей и рядов.
- •5. Степенные ряды
- •6. Ряд Тейлора
- •Исторические сведения
- •Абель
- •Адамар
- •Д’Аламбер
- •Больцано
- •Вейерштрасс
- •Дирихле
- •Коши
- •Лаплас
- •Лейбниц
- •Ньютон
- •Сильвестр
- •Тейлор
Глава 1 |
|
|
|
43 |
Функции нескольких переменных |
|||||
|
|
|
|
|
|
|
|
|
|
|
ç |
|
|
|
|
|
|
|
|
|
è |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Тейлор |
|
|
|
|
|
|
|
|
||
|
|
∂ |
(2x3 y − y5 |
−3x3 |
+5x2 −7x +3) = 6x2 y −9x2 +10x −7 , |
|||||
|
|
∂x |
||||||||
|
|
|
|
|
|
|
|
|
||
из формулы для нахождения производной находим, что |
||||||||||
|
|
|
|
|
′ |
= − |
6x2 y −9x2 |
+10x −7 |
. |
|
|
|
|
|
|
y (x) |
2x3 −5y4 |
|
|||
|
|
|
|
|
|
|
|
|
||
11. Формула Тейлора для функций нескольких переменных
Предположим, что функция u = f (x, y) определена в некоторой окрестности U точки M0 (x0, y0 ) и имеет в этой окрестности непрерывные частные производные вплоть до порядка n +1 включительно. Зададим приращения ∆x , ∆y независимых переменных x и y , обладающие следующим свойством: для любого t , −1≤t ≤1 точка (x0 +t ∆x, y0 +t ∆y) принадлежит окрестности U . Рассмотрим функцию
F(t) = f (x0 +t ∆x, y0 +t ∆y), −1≤t ≤1.
Заметим, что F(1) = f (x0 + ∆x, y0 + ∆y), F(0) = f (x0, y0 ) . Функция F непрерывно дифференцируема на отрезке [−1,1]. Действительно, по формуле для производной сложной функции находим:
′ |
∂f |
|
|
|
∂f |
|
|
|
|
F (t) = |
∂x |
(x0 |
+t ∆x, y0 |
+t ∆y) ∆x + |
∂y |
(x0 |
+t ∆x, y0 |
+t ∆y) ∆y. |
( ) |
Из теоремы о непрерывности сложной функции выводим, что функция
∂fx (x0 +t ∆x, y0 +t ∆y)
∂
непрерывна на отрезке [−1,1]. Отсюда и из непрерывности функции
∂fy (x0 +t ∆x, y0 +t ∆y)
∂
на отрезке [−1,1] следует непрерывность на указанном отрезке функции F′(t). Кроме того, полагая в формуле ( ) t = 0, находим:
Глава 1 |
44 |
Функции нескольких переменных |
||
|
|
|
|
|
ç |
|
|
|
è |
|
|
|
|
|
′ |
|
∂f |
|
|
|
∂f |
|
|
F (0 |
= |
∂x |
()x0 |
+ ∆x, y0 |
+ ∆y) ∆x + |
∂y |
(x0 |
+ ∆x, y0 + ∆y) ∆y. |
Далее находим:
|
|
′′ |
|
∂2 f |
(x0 +t ∆x, y0 +t ∆y) (∆x) |
2 |
+ |
||
|
|
F (t) = |
∂x2 |
|
|||||
|
|
|
|
|
|
|
|
|
|
+2 |
∂2 f |
(x +t ∆x, y +t ∆y) ∆x∆y + |
∂2 f |
(x +t ∆x, y +t ∆y) (∆y)2. |
|||||
|
∂y2 |
||||||||
|
∂x∂y 0 |
0 |
|
|
0 |
|
0 |
||
По причинам, аналогичным указанным выше, функция F′′(t) непрерывна на отрезке [−1,1]. Кроме того, имеет место равенство
|
|
′′ |
= |
∂2 f |
(x0 + ∆x, y0 + ∆y) (∆x) |
2 |
+ |
||
|
|
F (0) |
∂x2 |
|
|||||
|
|
|
|
|
|
|
|
|
|
+2 |
∂2 f |
(x + ∆x, y + ∆y) ∆x∆y + |
∂2 f |
(x + ∆x, y + ∆y) (∆y)2. |
|||||
|
∂y2 |
||||||||
|
∂x∂y 0 |
0 |
|
|
0 |
|
0 |
||
Так же доказывается, что и следующие производные функции F вплоть до производной порядка n +1 непрерывны на указанном отрезке. Применяя к функции F формулу Тейлора в точке t = 0 с остаточным членом в форме Лагранжа, получаем:
F(t) = F(0) + |
|
F′(0) |
t + |
F′′(0) |
t |
2 |
+ + |
|
F(n) (0) |
t |
n |
+ |
|
F(n+1) |
(θt) |
||||
|
1! |
|
2! |
|
|
|
n! |
|
|
(n + |
1)! |
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
для некоторого θ , 0 <θ <1. Отсюда находим: |
|
|
|
|
|
|
|
|
|||||||||||
F(1) = F(0) |
+ F′(0) |
+ F′′(0) |
+ + |
F(n) (0) |
+ |
F(n+1) (θ) . |
|
( ) |
|||||||||||
|
|
|
1! |
2! |
|
|
|
|
n! |
|
|
(n +1)! |
|
F (0), на- |
|||||
Подставляя сюда найденные выше значения F(1), |
F(0) |
, F (0) , |
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
′ |
|
|
′′ |
ходим первые три члена формулы Тейлора для функции двух переменных:
f(x0 + ∆x, y0 + ∆y) = f (x0, y0 ) +
+∂fx (x0 + ∆x, y0 + ∆y) ∆x + ∂fy (x0 + ∆x, y0 + ∆y) ∆y +
∂ ∂
Глава 1 |
45 |
Функции нескольких переменных |
||
|
|
|
|
|
ç |
|
|
|
è |
|
|
|
|
|
+ |
1 |
|
|
∂2 f |
(x , y ) (∆x)2 |
+ 2 |
∂2 f |
(x , y ) ∆x∆y + |
||||||||
|
|
|
∂x2 |
|
|
|||||||||||
2! |
∂x∂y |
|||||||||||||||
|
|
0 0 |
|
|
|
|
0 0 |
|||||||||
|
|
|
|
|
+ |
∂ |
2 |
f (x , y |
|
) (∆y)2 |
|
+ . |
||||
|
|
|
|
|
|
0 |
|
|||||||||
|
|
|
|
|
|
∂y2 |
0 |
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||
Можно выписать также следующие члены указанной формулы. Ограничиваясь в формуле ( ) случаем n =1, можно записать сле-
дующий вариант формулы Тейлора для функций двух переменных:
f(x0 + ∆x, y0 + ∆y) = f (x0, y0 ) +
+∂fx (x0, y0 ) ∆x + ∂fy (x0, y0 ) ∆y +
∂ ∂
+ |
1 |
|
|
∂2 f |
(x +θ∆x, y +θ∆y) (∆x)2 + 2 |
∂2 f |
(x +θ∆x, y +θ∆y) ∆x∆y + |
||||
|
|
|
∂x2 |
|
|||||||
2! |
∂x∂y |
||||||||||
|
|
0 |
0 |
|
0 |
0 |
|||||
|
|
|
|
|
+ |
∂2 f |
(x0 +θ∆x, y0 +θ∆y) (∆y)2 , |
|
|||
|
|
|
|
|
|
∂y2 |
|
|
|
|
|
где 0 <θ <1.
Последняя формула имеет место и в случае функций произвольного числа переменных. Предположим, что функция f определена в некоторой
окрестности U точки x0 n и имеет в этой окрестности непрерывные частные производные вплоть до второго порядка включительно. Выберем такое ∆x n , что для любогоt [−1,1] x0 +t∆x U . Введем в рассмотрение координаты вектора ∆x :
∆x = (∆x1,∆x2, ,∆xn ) .
Тогда имеет место следующее равенство
n |
∂f (x |
) |
|
f (x0 + ∆x) = f (x0 ) + ∑ |
0 |
|
∆xk + |
∂x |
|
||
k=1 |
k |
|
|
Глава 1 |
46 |
Функции нескольких переменных |
||
|
|
|
|
|
ç |
|
|
|
è |
|
|
|
|
|
+ |
1 |
|
n |
∂2 f (x +θ∆x) |
(∆xk ) |
|
n n |
∂2 f (x +θ∆x) |
|
, |
|
2 |
|
∑ |
∂x2 |
2 |
+ 2∑∑ |
∂x |
∂x |
∆xk ∆xl |
|||
|
|
|
|
0 |
|
|
0 |
|
|
|
|
|
|
k=1 |
k |
|
|
k=1 l=2 |
k |
l |
|
|
|
для некоторого θ , 0 <θ <1.
12. Экстремумы функций нескольких переменных
Определения точки максимума, минимума и экстремума в случае функций нескольких переменных аналогичны случаю функций одной пе-
ременной. Напомним эти определения. |
|
|
|
Предположим, |
что функция f определена в некоторой окрестнос- |
||
ти U n точки a . |
|
|
|
ОПРЕДЕЛЕНИЕ. |
Если существует такая окрестность U0 U точки a , |
||
что для всех x U0 |
выполняется неравенство |
f (x) ≤ f (a) , говорят, что |
|
функция f имеет в точке a локальный максимум. Если для всех |
x U0 , |
||
x ≠ a выполняется неравенство f (x) < f (a) , говорят, что функция f |
имеет |
||
в точке a строгий локальный максимум. |
|
|
|
ОПРЕДЕЛЕНИЕ. |
Если существует такая окрестность U0 U точки a , |
||
что для всех x U0 |
выполняется неравенство |
f (x) ≥ f (a) , говорят, что |
|
функция f имеет в точке a локальный минимум. Если для всех |
x U0 , |
||
x ≠ a выполняется неравенство f (x) > f (a), говорят, что функция f |
имеет |
||
в точке a строгий локальный минимум.
Если функция f имеет в точке a локальный максимум или минимум, говорят, что эта функция имеет в точке a локальный экстремум. Аналогично понятия строгого локального максимума и минимума «объединяются» в понятие строгого локального экстремума.
Дадим сначала необходимое условие существования экстремума. Напомним следующий факт. Предположим, что функция f одной пере-
Глава 1 |
47 |
Функции нескольких переменных |
||
|
|
|
|
|
ç |
|
|
|
è |
|
|
|
|
|
менной имеет в некоторой точке a локальный экстремум. Если эта функция дифференцируема в точке a , то f ′(a) = 0 . Этим свойством мы будем пользоваться в доказательстве следующего утверждения.
ТЕОРЕМА 12. Предположим, что функция f определена в некоторой
окрестности точки a n и имеет в этой точке локальный экстремум. Если в этой точке функция имеет частные производные первого порядка, то все эти производные равны нулю.
ДОКАЗАТЕЛЬСТВО. Ограничимся случаем функции двух переменных. Предположим, что a = (a1,a2 ). Рассмотрим функцию g(x1) = f (x1,a2 ) одной переменной. Эта функция определена в некоторой окрестности точки a1 и имеет в точке a1 локальный экстремум. Кроме того, существует
g′(a1) = ∂∂fx (a1,a2 ) .
Тогда имеет место равенство g′(a1) = 0 , то есть ∂∂fx (a1,a2 ) = 0. Аналогично
рассматривается частная производная по второй переменной. Теорема доказана.
ОПРЕДЕЛЕНИЕ. Точка, в которой все частные производные первого порядка функции f обращаются в ноль, называется стационарной точкой этой функции.
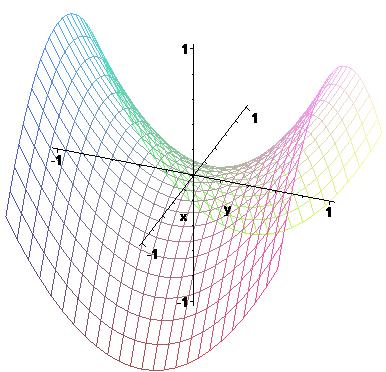
ЗАМЕЧАНИЕ. Как и в случае функций одной переменной, стационарная точка может не быть точкой экстремума. Например, для функции f (x, y) = x2 − y2 точка (0,0) является стационарной, f (0,0) = 0 . Однако в любой окрестности рассматриваемой точки функция может принимать как положительные, так и отрицательные значения. Например, для любого ε ≠ 0 имеем: f (ε,0) =ε2 > 0, f (0,ε) = −ε2 < 0 . Поверхность z = x2 − y2 в окрестности начала координат изображена на следующем рисунке.
Глава 1 |
48 |
Функции нескольких переменных |
||
|
|
|
|
|
ç |
|
|
|
è |
|
|
|
|
|
Перейдем к достаточным условиям существования локального экстремума. Эти условия основываются на теории квадратичных форм. Напомним некоторые результаты этой теории.
ОПРЕДЕЛЕНИЕ. Квадратичной формой от n переменных называется функция f (x1, x2, , xn ) следующего вида:
n n
f (x1, x2, , xn ) = ∑∑aij xi xj ,
i=1 j=1
где aij , 1≤i, j ≤ n — вещественные числа.
При i ≠ j указанная сумма имеет два подобных слагаемых, aij xi xj и a ji xj xi . Всегда предполагается, что для таких значений индексов выполня-
ется соотношение aij = a ji (что не уменьшает рассматриваемый класс функций), и квадратичная форма после приведения подобных может быть записана следующим образом:
n |
n−1 n |
f (x1, x2, , xn ) = ∑aii xi2 |
+ ∑ ∑ aij xi xj. |
i=1 |
i=1 j=i+1 |

Глава 1 |
49 |
Функции нескольких переменных |
||
|
|
|
|
|
ç |
|
|
|
è |
|
|
|
|
|
Сильвестр
Симметричная матрица
|
a11 |
a12 |
a1n |
|
|||
A = |
a |
a |
a |
|
, |
||
|
21 |
22 |
|
|
2n |
||
|
|
|
|
|
|
||
|
|
|
an2 |
|
|
|
|
|
an1 |
ann |
|
||||
называется матрицей указанной квадратичной формы. |
|||||||
Квадратичная форма f |
|
называется положительно (отрицательно) |
|||||
определенной, если для любого ненулевого вектора x n имеет место не-
равенство f (x) > 0 ( f (x) < 0 ). |
|
|
|
|
|
|
|
|
|
|
||||||||
|
Квадратичная форма называется неопределенной, если существуют |
|||||||||||||||||
векторы x1 , |
x2 n , для которых |
f (x1) > 0 и |
f (x2 ) < 0. |
|
|
|
||||||||||||
|
Например, |
квадратичная форма |
f (x , x ) = x2 |
+ x2 |
является положи- |
|||||||||||||
|
|
|
|
|
|
|
|
|
|
1 |
|
|
2 |
1 |
2 |
|
|
|
тельно определенной, |
g(x , x ) = −(x2 + x2 ) — отрицательно определенной, |
|||||||||||||||||
|
|
|
|
|
1 |
|
2 |
|
1 |
2 |
|
|
|
|
|
|
|
|
а h(x , x ) = x2 − x2 — неопределенной. |
|
|
|
|
|
|
|
|
|
|||||||||
1 |
2 |
1 |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Напомним теперь критерий положительной определенности. Квад- |
|||||||||||||||||
ратной матрице A указанного выше вида поставим в соответствие следую- |
||||||||||||||||||
щие ее миноры порядков 1, 2, …, n : |
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
a11 |
a12 |
|
|
a11 |
a12 |
a13 |
|
|
|
a11 |
a1n |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|||||||||||||
|
|
a , |
|
, |
|
a |
a |
a |
|
, , |
|
|
|
|
, |
|||
|
|
11 |
|
a21 |
a22 |
|
|
21 |
22 |
23 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a31 |
a32 |
a33 |
|
|
|
an1 |
ann |
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
называемые ее главными угловыми минорами.
ТЕОРЕМА (КРИТЕРИЙ СИЛЬВЕСТРА). Квадратичная форма f является положительно определенной тогда и только тогда, когда все главные угловые миноры ее матрицы являются положительными.
СЛЕДСТВИЕ. Квадратичная форма f является отрицательно определенной тогда и только тогда, когда ее главные угловые миноры удовлетворяют условиям:

Глава 1 |
50 |
Функции нескольких переменных |
||
|
|
|
|
|
ç |
|
|
|
è |
|
|
|
|
|
|
a11 |
a12 |
|
|
a11 |
a12 |
a13 |
|
|
|
|
|
|
||||||
|
|
||||||||
a < 0, |
|
> 0, |
a |
a |
a |
|
< 0, . |
||
11 |
a21 |
a22 |
|
|
21 |
22 |
23 |
|
|
|
|
|
a31 |
a32 |
a33 |
|
|
||
|
|
|
|
|
|
|
Рассмотрим частный случай квадратичной формы от двух переменных: f (x, y) = Ax2 + 2Bxy +Cy2 . Матрица этой квадратичной формы имеет
вид A B . Для анализа положительной определенности такой квадратич-
B C
ной формы можно воспользоваться критерием Сильвестра. Из его получаем:
квадратичная форма f (x, y) = Ax2 + 2Bxy +Cy2 является положи-
тельно определенной тогда и только тогда, когда A > 0 и AC − B2 > 0 .
Эти же результаты можно получить, не обращаясь к критерию Сильвестра, и сводя анализ значений, принимаемых квадратичной формой, к анализу значений, принимаемых квадратным трехчленом. Детальный анализ такого подхода предоставляется читателю.
Аналогично получается следующий результат:
квадратичная форма f (x, y) = Ax2 + 2Bxy +Cy2 является отрица-
тельно определенной тогда и только тогда, когда A < 0 и AC − B2 > 0 .
Нам потребуется также следующее утверждение.
ТЕОРЕМА 13. Квадратичная форма f (x, y) = Ax2 + 2Bxy +Cy2 явля-
ется неопределенной тогда и только тогда, когда AC − B2 < 0.
ДОКАЗАТЕЛЬСТВО. Предположим сначала, что A ≠ 0 . Имеет место тождество
Ax2 + 2Bxy +Cy2 = 1A ((Ax + By)2 + (AC − B2 )y2 ).

Глава 1 |
51 |
Функции нескольких переменных |
||
|
|
|
|
|
ç |
|
|
|
è |
|
|
|
|
|
Квадратичная форма f является неопределенной в том и только том случае, когда неопределенной является квадратичная форма
g(x, y) = (Ax + By)2 + (AC − B2 )y2 ,
которую мы и будем анализировать.
Предположим, что квадратичная форма g неопределенная. Тогда имеет место неравенство AC − B2 < 0. Действительно, в противном случае,
то есть, если AC − B2 ≥ 0, для любых x , |
y выполняются неравенства |
|||
(Ax + By)2 ≥ 0, (AC − B2 )y2 ≥ 0 |
|
|||
и, следовательно, g(x, y) ≥ 0 |
для любых значений x , y , что противоречит |
|||
условию неопределенности. |
|
|
|
|
Обратно. Предположим, |
что имеет место неравенство |
AC − B2 < 0. |
||
Существуют значения x0 , y0 , |
удовлетворяющие условиям |
Ax0 + By0 = 0, |
||
y0 ≠ 0 . Например, можно взять x0 = B , y0 = −A. Тогда |
|
|||
g(x , y ) = (AC − B2 ) y2 < 0. |
|
|||
0 |
0 |
0 |
|
|
|
|
<0 |
>0 |
|
С другой стороны, g(x,0) = A2x2 > 0 для любого x ≠ 0. Квадратичная форма g может принимать значения разных знаков и, следовательно, является неопределенной.
Мы доказали, что в предположении A ≠ 0 квадратичная форма f
является неопределенной в том и только том случае, когда AC − B2 < 0. В случае C ≠ 0 с помощью тождества
Ax2 + 2Bxy +Cy2 = C1 ((Bx +Cy)2 + (AC − B2 )x2 )
аналогично доказывается, что неопределенность квадратичной формы f
равносильна условию AC − B2 < 0.
Глава 1 |
52 |
Функции нескольких переменных |
||
|
|
|
|
|
ç |
|
|
|
è |
|
|
|
|
|
Рассмотрим случай A =C = 0 . Квадратичная форма f принимает вид f (x, y) = 2Bxy . Неравенство AC − B2 < 0 в данном случае равносильно неравенству B2 > 0 , то есть условию B ≠ 0 . Легко видеть, что последнее условие равносильно неопределенности квадратичной формы f . Действительно, если B = 0, то функция f является тождественно нулевой, и не является неопределенной квадратичной формой. Если B ≠ 0 , то в некоторых точках функция f принимает значения разных знаков, например,
f (1,1) = 2B, f (1,−1) = −2B.
Итак, при любых предположениях относительно A и C условие AC − B2 < 0 необходимо и достаточно для неопределенности рассматриваемой квадратичной формы.
Теорема доказана.
Из приведенных выше критериев положительной и отрицательной определенности и неопределенности квадратичных форм от двух переменных немедленно вытекает следующий результат.
ТЕОРЕМА 14. Предположим, что квадратичная форма
f (x, y) = A x2 + 2B xy +C y2 |
||
0 |
0 |
0 |
является положительно определенной. |
Тогда существует такое ε > 0, |
|
что для любых значений A, B , C , удовлетворяющих условиям |
||
| A − A0 |<ε, | B − B0 |<ε, |
| C −C0 |<ε, |
|
квадратичная форма Ax2 + 2Bxy +Cy2 |
является положительно опреде- |
|
ленной. Аналогичное утверждение справедливо для случаев отрицательно определенных и неопределенных квадратичных форм.
ЗАМЕЧАНИЕ. Утверждение, аналогичное сформулированной теореме, справедливо и для случая квадратичных форм от произвольного числа переменных. Перейдем теперь к достаточным условиям существования экстремума функции нескольких переменных.
Глава 1 |
53 |
Функции нескольких переменных |
||
|
|
|
|
|
ç |
|
|
|
è |
|
|
|
|
|
Предположим, что функция f определена и непрерывна вместе со своими частными производными первого и второго порядка в некоторой окрестности точки a n . Рассмотрим симметричную матрицу
|
∂2 f |
|
|
|
|
∂2 f |
|
|
|
|
∂2 f |
|
|
|
||||||||
|
∂x2 |
(a) |
|
|
|
|
|
|
(a) |
|
|
|
|
|
(a) |
|||||||
|
∂x |
∂x |
∂x |
∂x |
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
1 |
|
|
|
1 |
|
2 |
|
|
|
1 |
|
n |
|
|
||||||
|
∂ |
2 |
f |
|
|
|
|
∂ |
2 |
f |
|
|
|
|
∂ |
2 |
f |
|
|
|
||
|
|
|
|
(a) |
|
|
(a) |
|
|
|
|
(a) |
||||||||||
∂ ∂ |
|
|
|
|
2 |
∂ |
|
∂ |
|
|||||||||||||
A = |
|
|
|
|
|
|
|
|
|
|
|
|
|
. |
||||||||
|
x1 |
x2 |
|
∂x2 |
|
|
|
|
x2 |
|
xn |
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
∂2 f |
|
|
|
|
∂2 f |
|
|
|
|
∂2 f |
|
|
|
||||||||
|
|
|
|
|
|
|
(a) |
|
|
|
|
|
|
(a) |
∂x2 (a) |
|
||||||
|
∂x ∂x |
|
|
∂x ∂x |
|
|||||||||||||||||
|
|
|
|
|
||||||||||||||||||
|
1 |
n |
2 |
|
n |
|
|
|
|
n |
|
|
|
|||||||||
Соответствующую ей квадратичную форму от n переменных обозначим через g .
В этих предположениях и обозначениях справедливо следующее утверждение.
ТЕОРЕМА 15. Предположим, что выполняются равенства
∂f |
(a) = 0, |
∂f |
(a) = 0, , |
∂f |
(a) = 0 . |
|
∂x |
∂x |
∂x |
||||
|
|
|
||||
1 |
|
2 |
|
n |
|
Тогда
1)если квадратичная форма g является положительно определенной, то функция f имеет в точке a строгий локальный минимум;
2)если квадратичная форма g является отрицательно определенной, то функция f имеет в точке a строгий локальный максимум;
3)если квадратичная форма g является неопределенной, то функция f не имеет в точке a экстремума.
ДОКАЗАТЕЛЬСТВО. В доказательстве мы ограничимся случаем функции двух переменных и детально рассмотрим только пункт 1).
Глава 1 |
54 |
Функции нескольких переменных |
||
|
|
|
|
|
ç |
|
|
|
è |
|
|
|
|
|
Предположим, что для функции f (x, y), определенной и непрерывной вместе со своими частными производными первого и второго поряд-
ков в некоторой окрестности U 2 |
точки (a,b) выполняются условия |
|
||
∂f |
(a,b) = 0, |
∂f |
(a,b) = 0 |
( ) |
∂x |
|
∂y |
|
|
Выберем приращения ∆x , ∆y независимых переменных, такие что для любого t [−1,1] точка (a +t ∆x,b +t ∆y) принадлежит окрестности U . Тогда с учетом соотношений ( ), из разложения функции f по формуле Тейлора получаем:
|
|
|
|
|
f (a + ∆x,b + ∆y) − f (a,b) = |
|||
= |
1 |
|
|
∂2 f |
(a +θ∆x,b +θ∆y) (∆x)2 + 2 |
∂2 f |
(a +θ∆x,b +θ∆y) ∆x∆y + |
|
|
|
|
∂x2 |
|
||||
2! |
∂x∂y |
|||||||
|
|
|
|
|||||
+ |
∂ |
2 |
f |
(a +θ∆x,b +θ∆y) (∆y)2 |
|
|
. |
||||
|
∂y2 |
|
|
||
Предположим, что квадратичная форма с матрицей
|
∂2 f |
|
∂2 f |
|
||
|
∂x2 |
(a,b) |
|
|
(a,b) |
|
∂x∂y |
||||||
|
|
|
||||
|
∂2 f |
|
∂2 f |
|
||
|
|
(a,b) |
|
2 |
|
|
|
|
|||||
|
∂x∂y |
∂y |
(a,b) |
|||
|
|
|
|
|||
является положительно определенной. В силу непрерывности частных производных второго порядка в точке (a,b) , существует такое ε > 0, что
для любых ∆x , |
∆y , удовлетворяющих условию | ∆x |<ε , | ∆y |<ε , квадра- |
||||||
тичная форма с матрицей |
|
|
|
||||
|
∂2 f |
|
|
∂2 f |
|
||
|
∂x2 |
|
(a +θ ∆x,b +θ ∆y) |
|
|
(a +θ ∆x,b +θ ∆y) |
|
∂x∂y |
|||||||
|
|
|
|
||||
|
∂2 f |
|
|
∂2 f |
|
||
|
|
|
(a +θ ∆x,b +θ ∆y) |
|
2 |
|
|
|
|
|
|||||
|
∂x∂y |
|
∂y |
(a +θ ∆x,b +θ ∆y) |
|||
|
|
|
|
|
|||
Глава 1 |
55 |
Функции нескольких переменных |
||
|
|
|
|
|
ç |
|
|
|
è |
|
|
|
|
|
будет положительно определенной. Следовательно, для ∆x , ∆y , удовле-
творяющих условиям | ∆x |<ε , |
| ∆y |<ε , и не равных одновременно нулю, |
|||
выполняется неравенство |
|
|
|
|
∂2 f (a +θ∆x,b +θ∆y) (∆x)2 + 2 |
∂2 f |
(a +θ∆x,b +θ∆y) ∆x∆y + |
||
∂x∂y |
||||
∂x2 |
|
|
||
+∂2 f (a +θ∆x,b +θ∆y) (∆y)2 > 0, ∂y2
то есть f (a + ∆x,b + ∆y) − f (a,b) > 0 . Это означает, что в точке (a,b) функция f имеет строгий локальный минимум.
Теорема доказана.
Ограничиваясь случаем функций двух переменных, переформулируем полученное утверждение в терминах производных функции f . Как и
выше, считаем, что точка (a,b) 2 является стационарной для функции f . Введем обозначения
A = |
∂2 f |
(a,b), B = |
∂2 f |
(a,b), C = |
∂2 f |
(a,b). |
|
∂x2 |
∂x∂y |
∂y2 |
|||||
|
|
|
|
Тогда утверждение теоремы может быть переформулировано так:
1)если A > 0 и AC − B2 > 0 , то функция f имеет в точке (a,b) строгий минимум;
2)если A < 0 и AC − B2 > 0 , то функция f имеет в точке (a,b) строгий максимум;
3)AC − B2 > 0 , то функция f не имеет в точке (a,b) экстремума.
ПРИМЕР. Рассмотрим функцию f (x, y) = x3 + y3 −3xy , x , y . То-
гда
∂f (x, y) |
=3x2 −3y, |
∂f (x, y) |
=3y2 −3x. |
∂x |
|
∂x |
|
Глава 1 |
56 |
Функции нескольких переменных |
||
|
|
|
|
|
ç |
|
|
|
è |
|
|
|
|
|
Из системы уравнений |
∂f (x, y) |
= 0 , ∂f (x, y) |
= 0 получаем соотношения |
|
|
∂x |
|
∂y |
|
|
x2 = y, |
y2 = x. |
||
Отсюда следует, что рассматриваемая функция имеет две стационарные точки M1(0,0) и M2 (1,1).
Анализируем точку (0,0). Из равенств
∂2 f (x, y) |
= 6x, |
∂ |
2 f (x, y) |
= −3, |
∂f (x, y) |
= 6y |
∂x2 |
|
∂x∂y |
∂x |
|||
|
|
|
|
|||
следует, что A = 0, B = −3, C = 0 . Тогда AC − B2 = −9 , и функция не имеет |
||||||
экстремума в данной точке. |
|
|
|
|
|
|
Для точки (1,1) находим: |
A = 6, B = −3, |
C = 6 , выполняются соот- |
||||
ношения A > 0, AC − B2 > 0 , |
и в этой точек функция имеет локальный |
|||||
максимум. |
|
|
|
|
|
|
