Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Челябинский Государственный Университет

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

rsu594.pdf

Скачиваний:

Добавлен:

23.03.2015

Размер:

2.17 Mб

Скачать

☆

<<< < Предыдущая 1 2 3 4 5 6 7 8 910 / 1610 11 12 13 14 15 16 > Следующая >>>

Глава 2	74	Функциональные ряды

ç				è


Абель			Дирихле

Отметим, что ни одну из этих стрелок нельзя обратить, например, из поточечной сходимости, вообще говоря, не вытекает равномерная сходимость и так далее.

3. Признаки Абеля и Дирихле

Приводимые ниже признаки являются аналогами признаков Абеля и Дирихле для случая числовых рядов.

Напомним сначала следующее утверждение.

ТЕОРЕМА 5. Предположим, что n , {ak }nk=1 — монотонная число-

вая последовательность, {bk }nk=1 — произвольная числовая последовательность. Тогда имеет место оценка

∑akbk

k=1

≤ (| a1 | +2 | an |) max ∑bi .

1≤k≤n i=1

Указанное в теореме неравенство называется неравенством Абеля.

ТЕОРЕМА 6 (ПРИЗНАК ДИРИХЛЕ). Предположим, что для функцио-

+∞

нального ряда ∑an (x)bn (x) , x I выполняются следующие условия:

n=1

1) для каждого x I числовая последовательность {an (x)}n+∞=1 явля-

ется монотонной;

2) an (x) 0 на промежутке I ;

3) существует такая константа M , что для всех n ≥1, x I имеет

место оценка

∑bk (x)

≤ M .

k=1

+∞

Тогда ряд ∑an (x)bn (x)

равномерно сходится на промежутке I .

n=1

ДОКАЗАТЕЛЬСТВО.

Для произвольных натуральных n , p и любого

x I из условия 3) теоремы получаем:

n+p

∑ bk (x)

∑bk (x) −∑bk (x)

≤

∑bk (x)

≤ 2M.

k=n+1

k=1

Воспользуемся условием 2) формулировки теоремы. Выберем произвольное ε > 0 и найдем такое N , что при n ≥ N для всех x I выполняется неравенство | an (x) |<ε . Применяя для произвольного фиксированного x I

неравенство Абеля к числовым последовательностям

{ak (x)}nk+=np+1 и {bk (x)}nk+=np+1,

находим:

Глава 2	75	Функциональные ряды

ç			è

n+p

∑

k=n+1

ak (x)bk (x) ≤ (| an+1(x) | +2 | an+p (x) |)

<3ε

n+q

max ∑ ak (x)bk (x) ≤ 6εM .

1≤q≤p k=n+1

≤2M

В силу произвольности ε , из критерия Коши равномерной сходимости функционального ряда выводим равномерную сходимость ряда

+∞

∑an (x)bn (x) .

n=1

Теорема доказана.

ЗАМЕЧАНИЕ. Условие 2) формулировки теоремы может быть пере-

+∞

формулировано так: частичные суммы ряда ∑bn (x) равномерно ограни-

n=1

чены на промежутке I .

СЛЕДСТВИЕ ПРИЗНАКА ДИРИХЛЕ. Предположим, что последовательность функций {an}+∞n=1, определенных на промежутке I , удовлетворяет следующим условиям:

1) для любого x I числовая последовательность {an (x)}n+∞=1 являет-

ся монотонной;

2) an (x) 0 на промежутке I .

+∞

Тогда функциональный ряд ∑(−1)n−1an (x) равномерно сходится на про-

n=1

межутке I .

Это утверждение вытекает из признака Дирихле, если положить

bn (x) = (−1)n−1, n , x I .

Отметим, что приведенное следствие является аналогом (для случая функциональных рядов) признака Лейбница сходимости числового ряда.

				+∞	(−1)n−1 xn
ПРИМЕР. Доказать равномерную сходимость ряда ∑						α на
промежутке 0 ≤ x ≤1 при любом α > 0.				n=1	(n	+ x)
промежутке 0 ≤ x ≤1 при любом α > 0.
РЕШЕНИЕ. Полагаем
a (x) =	1	,	b (x) = (−1)n−1 xn ,	n =1,2, 0 ≤ x ≤1
a (x) =	α	,	b (x) = (−1)n−1 xn ,	n =1,2, 0 ≤ x ≤1
n	α		n
	(n + x)

При любом фиксированном x [0,1] последовательность {an (x)}n+∞=1 является убывающей. Из оценки

an (x) ≤	1	, n , 0 ≤ x ≤1
	α
	n

вытекает, что an (x) 0 на промежутке [0,1] .

Глава 2	76	Функциональные ряды

ç			è


	+∞
Частичные суммы ряда ∑bn (x) имеют вид
	n=1
n	n			n	x
Sn (x) = ∑bk (x) = ∑(−1)k−1 xk =		x −(−1)			x	.
Sn (x) = ∑bk (x) = ∑(−1)k−1 xk =						.
k=1	k=1		1+ x

Оценивая модуль числителя последней дроби сверху, а знаменатель снизу, получаем:

| x −(−1)n x |≤| x | +| (−1)n x |≤ 2, 1+ x ≥1.

Отсюда следует, что для любого x [0,1] имеет место неравенство | Sn (x) |≤ 2. Все условия признака Дирихле выполнены, следовательно, рассматриваемый ряд сходится на промежутке [0,1] равномерно.

Отметим в заключение, что при α >1 равномерная сходимость рассматриваемого ряда может быть выведена из признака Вейерштрасса. Действительно, для любого x [0,1] выполняется оценка

(−1)n−1 xn

≤

n =1,2, ,

(n + x)

поскольку для любого

x [0,1]

имеют

место

неравенство xn ≤1,

(n + x)α ≤ nα .

+∞

x [0,2π] и по-

ПРИМЕР. Рассмотрим функциональный ряд ∑sinαnx

n=1

кажем, что

1)при α >1 этот ряд сходится абсолютно и равномерно на отрезке

[0,2π];

2)при 0 <α ≤1 ряд сходится поточечно на отрезке [0,2π];

3)при 0 <α ≤1 ряд сходится равномерно на отрезке вида [δ,2π −δ]

при любом δ , 0 <δ <π ; 4) при 0 <α ≤1 ряд не сходится равномерно на любом отрезке вида

[0,δ], δ > 0.

РЕШЕНИЕ. 1) При α >1 члены рассматриваемого ряда мажорируются членами сходящегося числового ряда:

sinαnx	≤	1	, 0 ≤ x ≤ 2π,

		α
n		n

и по теореме Вейерштрасса рассматриваемый функциональный ряд сходится на промежутке [0,2π] абсолютно и равномерно.

Глава 2	77	Функциональные ряды

ç			è

Для дальнейшего анализа найдем сумму S = ∑sin kx . Умножая обе

k=1

части последнего соотношения на sin 2x , в предположении, что эта величина отлична от нуля, и учитывая тождества

sinα sin β =

(cos(α − β) −cos(α + β)),

β −α

β +α

cosα −cos β = 2cos

cos

получаем:

sin

S = ∑sin kx sin

∑ cos

k −

x −cos k

k=1

2 k=1

cos

−cos

+ cos

−cos

+ cos n −

−cos n +

(n +1)x

cos

−cos

n +

x =sin

sin

Отсюда получаем, что

sin nx

(n +1)x

sin

Вернемся теперь к анализу функционального ряда. В дальнейшем

всюду предполагаем, что 0 <α ≤1

2) Покажем, что рассматриваемый ряд поточечно сходится на про-

межутке [0,2π].

Если

x = 0 или

x = 2π ,

+∞

обращаются в

то все члены ряда ∑sinαnx

ноль, и ряд сходится.

n=1

Допустим, что 0 < x < 2π . Тогда 0 <

<π , sin

≠ 0 . Оцениваем час-

+∞

тичные суммы ряда ∑sin nx по найденной выше формуле:

n=1

sin nx

sin

(n +1)x

∑sin kx

≤

sin

k=1

Глава 2	78	Функциональные ряды

ç			è

При фиксированном x из указанного диапазона частичные суммы ряда ограничены. Подчеркнем, что в приведенной оценке слева находится произвольная частичная сумма ряда, поскольку n любое. В правой части находится величина, не зависящая от n . Далее, учитываем, что последователь-

ность {1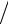nα}+∞n=1 монотонно сходится к нулю. По признаку Дирихле для чи-

+∞		сходится в точке x .
словых рядов ряд ∑sinαnx		сходится в точке x .
n=1	n

3) Выберем произвольное δ , 0 <δ <π и покажем, что ряд равномерно сходится на отрезке [δ,2π −δ]. В этом случае применяем признак Ди-

рихле равномерной сходимости функциональных рядов. Частичные суммы

+∞

ряда ∑sin nx оцениваем так:

n=1

∑sin kx

≤

sin

k=1

поскольку для x [δ,2π −δ] выполняется

оценка

≤

≤π −

и, сле-

довательно, sin 2x ≥sin δ2 . Чтобы применить признак Дирихле, снова учи-

тываем, что числовая последовательность {1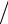nα}+∞n=1 монотонно сходится к нулю.

+∞		не сходится
4) Докажем теперь, что функциональный ряд ∑sinαnx		не сходится
n=1	n

равномерно на отрезке [0,δ] при любом δ > 0. Для этого покажем, что он не удовлетворяет критерию Коши равномерной сходимости. Для произ-

sin kx

вольного n ≥1 рассмотрим сумму

∑

и положим в ней x =

. Ве-

личина kx при изменении k

k=n+1

от n +1 до 2n возрастает и принимает значе-

ния от

n +1 >

до

2n = π ,

то

есть удовлетворяет условию

π < kx ≤

π .

Следовательно,

для указанных значений x и k выполняется

π , и тогда

неравенство sin kx >sin

∑ sinαkx

>sin

∑

k=n+1 k

Глава 2	79	Функциональные ряды

ç			è

Заметим теперь, что для всех значений k = n +1, n + 2 , …, 2n выполняется

неравенство kα ≤ k ≤ 2n					(здесь	учтено,	что		0 <α ≤1) и, следовательно,
1		≥	1	, и тогда
	kα	≥	2n	, и тогда	2n
	kα		2n
							1	= 1
				sin π	∑ ≥sin π n		1			sin π .	( )
				sin π	∑ ≥sin π n					sin π .	( )
				4	k=n+1	4	2n		2	4
Для любого δ > 0 при всех достаточно больших значениях n											величина

x = 21n попадает в промежуток [0,δ]. Из соотношения ( ) выводим, что для

рассматриваемого ряда не выполняется условие критерия Коши, и он не сходится равномерно.

ЗАМЕЧАНИЕ. Найденную выше сумму ∑sin kx можно было бы найти

k=1

по следующей схеме, использующей комплексные числа и формулу Эйлера:

eix = cos x +isin x, x .

Это означает, что cos x = Re(eix ) , sin x = Im(eix ) , где, как обычно, Re z и

Im z означают соответственно вещественную и мнимую части комплексного числа z . Тогда имеем:

1−ei(n+1)x

∑sin kx = ∑sin kx = Im

∑eikx

= Im

1−e

k=1

k=0

Упрощая последнее выражение

−ei(n+1)x

, находим искомую сумму. О т-

1−eix

сюда можно также найти значение суммы

∑coskx . Детали вычислений

предоставляются читателю.

k=0

ТЕОРЕМА 7 (ПРИЗНАК АБЕЛЯ). Предположим, что для функционально-

+∞

го ряда ∑an (x)bn (x) ,

x I

выполняются следующие условия:

n=1

числовая последовательность {an (x)}n+∞=1

1) для каждого x I

явля-

ется монотонной;

2) существует такая константа M , что для всех n , x I

име-

ет место оценка | an (x) |≤ M ;

Глава 2	80	Функциональные ряды

ç			è

+∞

3) ряд ∑bn (x) равномерно сходится на промежутке I .

n=1

+∞

Тогда функциональный ряд ∑an (x)bn (x) равномерно сходится на проме-

n=1

жутке I .

ДОКАЗАТЕЛЬСТВО. Применим к равномерно сходящемуся ряду

+∞

∑bn (x) критерий Коши равномерной сходимости ряда. Выберем произ-

n=1

вольное ε > 0. В силу этого критерия, существует такое N , что при n ≥ N для любых значений p =1, 2, … и всех x I выполняется неравенство

n+p

∑ bk (x) <ε .

k=n+1

Применяя для произвольного фиксированного x I неравенство Абеля к

числовым последовательностям {a (x)}n+p

и {b

(x)}n+p

, находим:

k=n+1

n+p

n+q

∑ ak (x)bk (x)

≤ (| an+1(x) | +2 | an+p (x) |) max

∑ ak (x)bk (x)

≤3Mε.

k=n+1

1≤q≤p

k=n+1

≤3M

<ε

В силу произвольности ε ,

из критерия Коши (равномерной сходимости

+∞

ряда) выводим равномерную сходимость ряда ∑an (x)bn (x) .

Теорема доказана.

n=1

ПРИМЕР. Доказать равномерную сходимость ряда

+∞ (−1)n−1 arctg nx

∑

, 0

≤ x < +∞

n=1

(n + x)

для произвольного α > 0.

+∞

(−1)n−1

РЕШЕНИЕ. Покажем сначала,

что функциональный ряд

∑n=1

(n + x)α

равномерно сходится на промежутке [0,+∞) . Это вытекает из следствия

признака Дирихле (аналога признака Лейбница). Действительно, достаточно заметить, что при любом x [0,+∞) числовая последовательность

1	+∞
1		является монотонной и из оценки
α		является монотонной и из оценки
(n + x)	n=1
			1	≤	1	, 0 ≤ x < +∞
			α	≤	α	, 0 ≤ x < +∞
			(n + x)		n

<<< < Предыдущая 1 2 3 4 5 6 7 8 910 / 1610 11 12 13 14 15 16 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
23.03.2015132.61 Кб156RitorikaZachet_2.doc
#
31.10.20183.05 Mб12Rock12.doc
#
23.03.2015654.34 Кб47rolshikov_v_e_modeli_upravleniya_zapasami.doc
#
22.11.201926.18 Кб3Rol_Rossii_v_deyatelnosti_Svyashennogo_soyuza_2...docx
#
08.03.20162.73 Mб27RPD_IOGP_ochnaya.doc
#
23.03.20152.17 Mб67rsu594.pdf
#
11.11.2019227.33 Кб29Russ_Stilistics.doc
#
23.03.201531.55 Кб21s.docx
#
23.03.2015828.93 Кб48Sachko_UMK_Istoria_polit_ucheny_ZR.doc
#
23.03.20152.54 Mб281Samouchitel_igry_na_snouborde.pdf
#
24.11.201950.12 Кб28Sanitarnaya_mikrobiologiaрр.docx