13

Чтобы найти

, подставим начальные условия в первое уравнение в (3.2):

.

(3.5)

Для того чтобы найти

, продифференцируем первое уравнение в (3.2):

Пример. Решить уравнение

при условиях

,

.

Из уравнения

находим

.

Чтобы найти

, продифференцируем уравнение:

Тогда

. Следовательно,

,

СР

Определение.

Функция

, определенная на множестве , называется периодиче-

ской, если существует число

такое, что

1)

;

2)

для любого

.

Число

называется периодом функции. Наименьший из всех положительных пе-

риодов функции называется основным периодом. Если - основной период функции, то

ее называют

-периодической.

Например, функции

и

являются

-периодическими, а функции

и

являются

-периодическими.

Чтобы построить график -периодической функции, достаточно построить его на

любом отрезке длиной

и затем продолжить график периодически на всю область опре-

деления.

Определение.

Периоды

и называются соизмеримыми, если существуют такие

натуральные числа

и

, что

.

14

Например, периоды

и

соизмеримы,

так как равенство

выполняется, например, при

, а

.

Теорема (о периодических функциях)

1.

Если функция

имеет период

, то функция

имеет период

.

2.

Пусть функции

и

имеют соизмеримые периоды

и

. Тогда функция

также является периодической функцией.

3.

Если функция

имеет период

и интегрируема на отрезке

,

то

при условии, что

,

.

Доказательство.

1.

Пусть функция

имеет период

, то есть

. И пусть

. Тогда

.

3.

Пусть функция

имеет период

:

. И пусть

(рис. 3.1). Тогда

.

T

Замечание.

Свойство 3

верно и

для отрица-

x1

T

x

тельных

значений периода:

a

x0 x1

x0 T

b

.

T

Рис. 3.1

Примеры

1.

. Поскольку

имеет период

, то

имеет период

.

2.

.

.

3.

. Периоды

и

соизмеримы, так как равенст-

во

выполняется, например, при

, а

. Следовательно, –

периодическая функция. Ее период равен

.

4.

. Периоды

и

несоизмеримы, так как равенст-

во

не выполняется ни при каких натуральных

и . Следователь-

но,

– непериодическая функция.

5.

–

и т.п.◄

Замечание. Пусть функция

–

-периодическая, функция

–

-периодическая.

Тогда наименьшее общее кратное этих периодов

будет периодом функ-

ции

,

,

. Но

не обязательно будет основным периодом.

Примеры

1.

- периодическая функция, но у нее нет основного перио-

да (наименьшего положительного).

2.

.

Функции

и

-

-периодические. Тогда

является периодом функции

. С другой стороны,

и по теореме о периодических функциях ее

период

.

15

Определение.

Гармоникой (гармоническим колебанием) называется функция ви-

да

или

,

(4.1)

где

,

– амплитуда колебания, 0

– начальная фаза,

– фаза, – круговая

(циклическая, угловая) частота.

Период колебания равен

. Число полных колебаний в единицу времени назы-

вается частотой и равно

.

Пример.

.

x

x 5cos 2t

5

3

Амплитуда колебаний равна

, началь-

ная фаза

, круговая частота

, период

2,5

колебания

.

/ 3

5 / 6

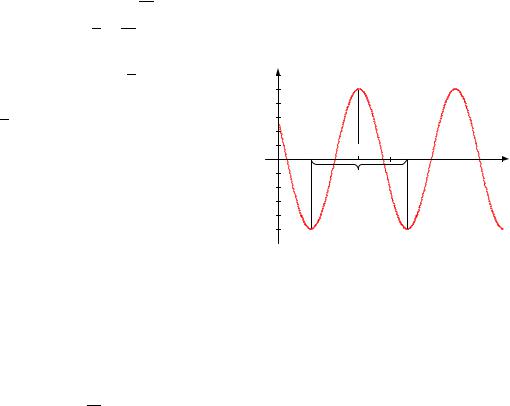
График функции в декартовой системе ко-

t

f(t)

ординат представлен на рис. 4.1◄

T

Запишем

функцию

5

иначе:

t

,

Рис. 4.1

где

,

.

Из гармоник можно составить ряд:

,

(4.2)

который является периодической функцией с периодом .

Гармонику

называют n -й гармоникой.

Ряд (4.2) можно также записать в виде:

где

,

,

.

l

1.

Если функция

является нечетной на отрезке [ l, l] ,

то f (x) dx 0 .

l

l

l

2.

Если функция

является четной на отрезке [ l, l] , то f (x) dx 2 f (x) dx .

l

0

Доказательство

t x

l

0

l

0

l

1.

f (x) dx f (x) dx f (x) dx f ( x) dx

f (x) dx

l

l

0

l

0

dx dt

0

l

l

l

f (t) dt f (x) dx f (x) dx f (x) dx 0 .

l

0

0

0

t x

l

0

l

0

l

2.

f (x) dx f (x) dx f (x) dx f ( x) dx f (x) dx

l

l

0

l

0

dx dt

16

0

l

l

l

l

f (t) dt f (x) dx f (x) dx f (x) dx 2

f (x) dx

l

0

0

0

0

Определение. Тригонометрическим рядом называется ряд вида

(n 1, 2,...)

.

(4.3)

Коэффициенты a0 , an ,bn

называются коэффициентами тригонометриче-

a0

f (x)

an cos n x bn sin n x .

(4.4)

2

n 1

Тогда коэффициенты ряда находятся по формулам

1

an

f (x) cos nx dx ,

n 0, 1,... ,

(4.5)

1

bn

f (x) sin nx dx,

n 1, 2,...

(4.6)

Доказательство. Пусть

f (x) - 2 -периодическая функция.

непрерывны,

то

ряд

можно

почленно интегрировать на отрезке

. Проинтегрируем обе части равенства (4.4).

f (x) dx

a0

dx

an cos n x bn sin n x dx .

2

n 1

Вычислим интегралы в правой части, учитывая лемму 1:

a0

dx a

;

2

0

a0

f (x) cos k x

cos k x an cos n x cos k x bn sin n x cos k x .

2

n 1

f (x) cos k x dx

a0

cos k x dx

an cos n x cos k x bn sin n x cos k x dx .

2

n 1

a0

1 a0

cos k x dx

sin k x

0 .

2

k

2

2

Если

n k , то

a

cos n x cos k x dx

a

cos 2

k x dx

an

1

cos 2kx dx

a

.

n

n

n

2

Если

n k , то

a

cos n x cos k x dx

an

cos(n k)x cos(n k)x dx 0 .

n

.

Следовательно,

f (x) cos n x dx an .

3) Найдем коэффициенты bn . Умножим обе части (4.4) на sin kx и проинтегрируем:

f (x) sin k x dx

a0

sin k x dx an cos n x sin k x bn sin n x sin k x dx .

2

n 1

Получим f (x) sin n x dx bn

Коэффициенты a0 , an ,bn

(n 1, 2,...) , вычисляемые по формулам (4.5), (4.6), называ-

a0

f (x) ~

an cos n x bn sin n x .

(4.7)

2

n 1

Определение. Функция

называется кусочно-монотонной на отрезке [a, b], если

этот отрезок можно разбить конечным числом точек x1 , x2 ,..., xn 1 на интервалы

(a, x1 ) ,

S(x

)

1

f (x

0) f (x

0) .

0

2

0

0

Пример. Дана периодическая функция с периодом 2 :

f (x) x,

x (рис.

4.2).