18
►По теореме 2 ряд Фурье для данной функции сходится во всех точках. Причем,
и |
|
|
|
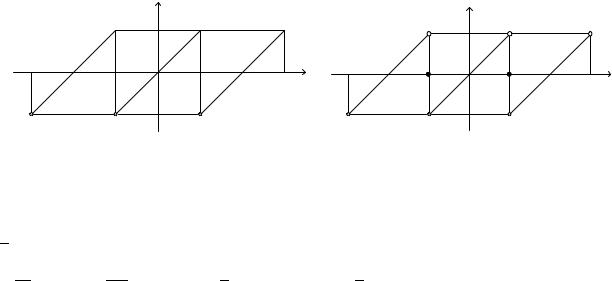
. График суммы ряда |
|
|
на рис. 4.3.
|
y |
|
|
|
y |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
x |
2 |
|
x |
|
|
2 |
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Рис. 4.2 |
|
|
|
Рис. 4.3 |
|
Найдем ряд Фурье. Поскольку функция является нечетной, то |
, |
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
.
|
( 1) |
n 1 |
2 sin 3 x |
|
|
|
x |
|
2 sin n x 2 sin x sin 2 x |
... |
x ( , ) . ◄ |
||
n |
|
3 |
||||
n 1 |
|
|
|
|
||
|
|
|
|
|
|
|
4.3.Разложение функции в ряд Фурье на произвольном промежутке
Пусть функция |
|
|
|
|
задана на промежутке |
|
. Сделав замену |
|
, получим |
|||||
|
|
|
|
|
||||||||||
функцию |
|
|
, где |
|
|
. Для функции |
имеет место формула (4.4): |
|||||||
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
a0 |
|
|
|
|
|
|
|
|
|
|
|
g( y) ~ |
an cos n y bn sin n y , |
|
|
||||||
|
|
|
|
|
2 |
|
|
|||||||
|
|
|
|
|
|
|
|
n 1 |
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
1 |
|
|
|
1 |
|
|
|
|
|
|
|
an |
|
g( y) cos ny dy , bn |
g( y)sin ny dy . |
|
|
|||||||
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Возвращаясь к переменной |
с помощью обратной замены |
|
|
, получим |
|||||||||||||||
|
|
||||||||||||||||||
|
|
|
|
|
a0 |
|
|
|
|
|
n x |
|
|
n x |
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
f (x) ~ |
|
an |
cos |
|
|
bn sin |
|
, |
|
|
|
|||||||
|
2 |
l |
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
n 1 |
|
|
|
|
|
|
l |
|
|
|
|||
|
|
1 l |
|
|
|
n x |
|
|
|
1 l |
|
|
n x |
|
|
|
|||
a |
l |
|
f (x) cos |
l |
dx , |
b |
l |
|
f (x)sin |
l |
dx . |
||||||||
|
|
|
|
|
|
|
|||||||||||||
n |
|
|
|
|
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
l |
|
|
|
|
|
|
|
|
|
l |
|
|
|
|
|
|
(4.8)
(4.9)
Замечание. По теореме о периодических функциях промежуток |
может быть |
|
заменен на любой другой промежуток длины , например, на |
или |
. |
4.4.Разложения только по синусам или только по косинусам
Разложение четной функции. Если функция |
является четной на отрезке |
, то |
|||
функция |
|
- четная, функция |
|
- нечетная и по лемме 1 из п. 4.2 |
|
|
|
|
|||
, |
|
|
|
, |
|
|
Следовательно, ряд Фурье четной функции содержит одни косинусы:
|
|
|
|
|
|
|
a0 |
|
|
|
n x . |
|||||
|
|
|
|
f (x) ~ |
|
an |
cos |
|||||||||
|
|
|
||||||||||||||
|
2 |
n 1 |
|
|
|
l |
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Разложение нечетной функции. |
Если функция - нечетная на отрезке |
|||||||||||||||
функция |
|
- нечетная, функция |
|
|
|
|
|
- четная. Тогда по лемме 1 |
||||||||
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
, |
|
|
|
|
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
Следовательно, ряд Фурье нечетной функции содержит одни синусы:
|
n x . |
f (x) ~ bn sin |
|
n 1 |
l |
|
19
(4.10)
(4.11)
, то
(4.12)
(4.13)
Произвольная функция. Пусть функцию , заданную на отрезке , требуется разложить в ряд только по косинусам. Доопределим функцию на промежутке так, чтобы получилась четная функция:
Для функции |
верно разложение (4.11) только по косинусам: |
|
||||||||||||||||
с коэффициентами |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
. |
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
||||||||
Поскольку на отрезке |
|
|
|
|
, то |
|
|
|||||||||||
и |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(4.14) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
для любого |
. |
(4.15) |
||||||
|
|
|
|
|
|
|
|
|
||||||||||
Аналогично можно разложить в ряд только по синусам функцию |
, заданную на |
|||||||||||||||||
отрезке [0, l]. Для этого ее нужно доопределить на промежутке |
|
так, чтобы получи- |
||||||||||||||||
лась нечетная функция: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Тогда
для любого |
, |
(4.16) |
где
(4.17)
Замечание. Оба разложения (4.15) и (4.16) верны только на отрезке [0, l].
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
20 |
|
|
|
|
|
|
1, |
x [0, |
/ 2], |
|
|
|
|
|
|
|
|
|||
Примеры. Дана функция |
f (x) |
x ( / 2, |
]. |
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
0, |
|
|
|
|
|
|
|
||||||
1. Разложить функцию в ряд только по синусам. По формулам (4.16), (4.17) получа- |
|||||||||||||||||||
ем: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
2 |
/ 2 |
|
2 |
|
|
|
n |
|
|
4 |
|
2 |
n |
|
bn |
|
|
f (x)sin nx dx |
|
sin nx dx |
|
|
cos |
|
1 |
|
|
sin |
|
|
, |
|||
|
|
|
|
|
n |
|
|
||||||||||||
|
|
0 |
|
0 |
|
n |
|
2 |
|
|
|
|
4 |
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
f (x) ~ bn |
sin |
n x bn sin nx |
4 |
|
sin 2 |
n sin nx , |
|
. |
|
|
||||||||||||
|
|
n |
|
|
|
|||||||||||||||||||
|
|
|
n 1 |
|
|
|
l |
|
n 1 |
|
|
|
|
n 1 |
|
4 |
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
2. |
Разложить функцию только по косинусам. По формулам (4.15), (4.14) получаем: |
|||||||||||||||||||||||
|
|
2 |
|
2 |
/ 2 |
|
|
|
2 |
|
|
|
|
|
|
2 |
/ 2 |
2 |
|
n |
|
|||
a0 |
|
f (x) dx |
|
dx 1, an |
|
|
f (x) cos nx dx |
cos nx dx |
sin |
, |
||||||||||||||
|
|
|
|
|
|
|
n |
2 |
||||||||||||||||
|
|
0 |
|
|
0 |
|
|
|
|
0 |
|
|
|
|
|
0 |
|
|
||||||
|
|
|
|
|
|
|
|
1 |
|
2 |
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
f (x) ~ |
|
|
sin |
2 cos nx |
|
|
|
◄ |
|
|
|
|
|||||||
|
|
|
|
|
2 |
n |
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
n 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|