7.6. Прогноз

Коли параметри економетричної моделі оцінюються узагальненим методом найменших квадратів, проблема прогнозування потребує спеціального дослідження. Це пов’язано з тим, що залишки моделі можуть мати систематичну складову, яку необхідно враховувати в точковому прогнозі.

Нехай колиде

Задача зводиться до того, щоб передбачити значення залежної змінної для заданого вектора. Можна записати

Місяць	Y	X1	X2	X3	u
3	38	57	17	99	1,398473
6	49	58	20	110	8,106768
1	39	62	22	104	–1,06351
2	41	65	25	109	–1,83599
4	42	66	27	114	–2,98904
5	44	69	28	116	–2,58705
8	45	70	30	116	–1,99326
7	44	72	32	119	–4,72569
9	48	75	34	114	0,03969
14	57	75	39	129	3,517828
11	49	77	33	124	–2,94188
10	51	79	35	120	–0,24083

, (7.25)

де — невідоме значення відхилень у прогнозований період. Нехай для

і(7.26)

а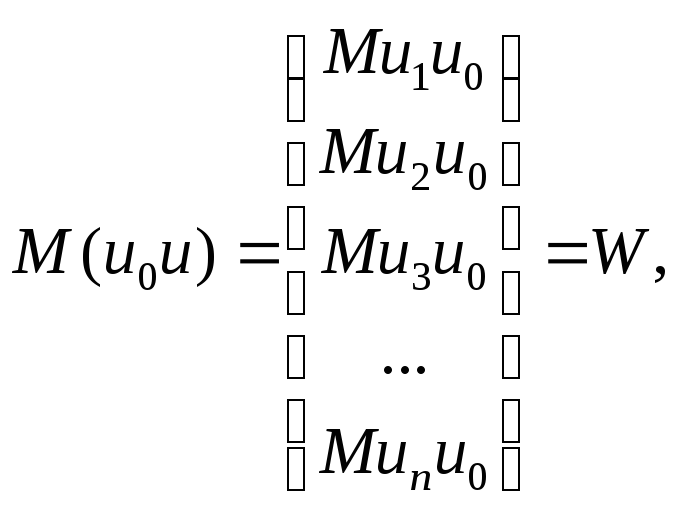(7.27)

де W — вектор коваріацій поточних і прогнозованих значень залишків.

Сформулюємо лінійний прогноз:

(7.28)

де с — n-вимірний вектор, який має мінімізувати дисперсію прогнозу:

. (7.29)

Мінімальне значення дисперсії прогнозу досягається для .

Враховуючи (7.25) і (7.28), можна записати відхилення

З умови незміщеності прогнозу випливає, що вектор с має задовольняти рівність

= 0. (7.30)

Тоді похибка прогнозу набере вигляду:

Оскільки — скаляр, то дисперсія прогнозу:

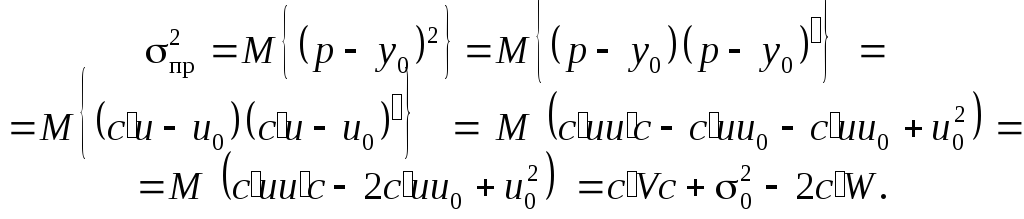(7.31)

Достовірним можна вважати прогноз тоді, коли дисперсія буде мінімальною. Тому формулюємо задачу:

мінімізувати (7.32)

за умови незміщеності прогнозу:

= 0.

Отже, для прогнозу можна використовувати співвідношення (7.33). Цей прогноз має дві особливості:

1) вектор прогнозних значень перемножується на вектор оцінок, обчислений згідно з узагальненим методом найменших квадратів;

2) для оцінювання невідомих прогнозних залишків застосовується матрицяV, яка містить інформацію про взаємозалежність залишків базисного періоду та прогнозних.

Розглянемо приклад побудови економетричної моделі узагальненим методом найменших квадратів за наявності гетероскедастичності.

Приклад 7.9 (ЛАБ). Побудуємо економетричну модель прибутку за умови, що в статистичній інформації (табл. 4.2) існує гетероскедастичність.

Розв’язання

1. Дослідимо гетероскедастичність на основі тесту Гольфельда—Квандта.

Алгоритм:

1. Вибираємо ту пояснювальну змінну, яка може викликати гетероскедастичність залишків. У даному випадку припусти- мо, що інвестиції можуть викликати гетероскедастичність за- лишків.

Сортуємо статистичну інформацію за змінною Х₁ (інвестиції)

2. Визначимо параметр c зі співвідношення:

,

де n — кількість спостережень (n = 20);

c — кількість спостережень, які необхідно в даному тесті відкинути всередині сукупності спостережень (c = 6).

3. Виділяємо дві сукупності спостережень (по сім спостережень) і за цими сукупностями будуємо економетричні моделі.

Скориставшись функцією «Лінійн» (програма Exсel), дістали такі результати для першої та другої сукупностей:

1,04837	–0,74008	–0,543	–26,4266
0,374765	1,633299	1,202374	69,22336
0,860598	1,995725	#Н/Д	#Н/Д
6,17349	3	#Н/Д	#Н/Д
73,76553	11,94876	#Н/Д	#Н/Д

Сума квадратів залишків становить

4. Розраховуємо критерій R^*

.

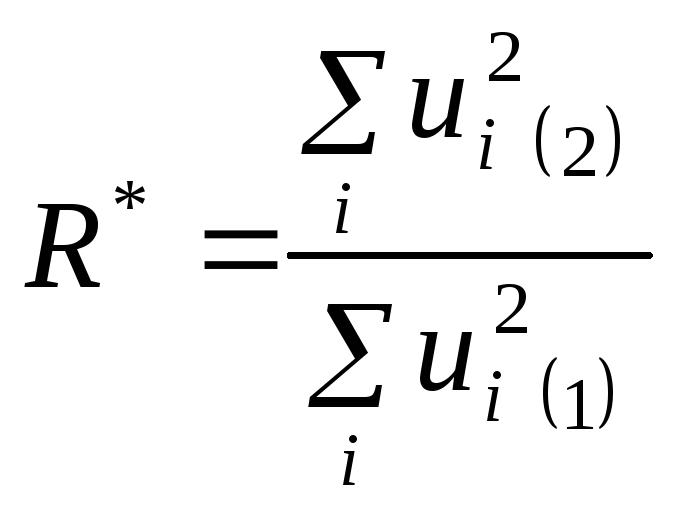Порівняємо його з критичним значенням F-критерію для обраного рівня значущості (0,05) і ступеня свободи (n – c)/2 – m.

R^* = 0,213659; F_крит = 9,276619.

Оскільки R^* < F_крит (0,21 < 9,28), то інвестиції не викликають гетероскедастичність залишків, тобто зміна дисперсії залишків не може викликатися зміною цієї пояснювальної змінної.

Тест Глейзера. На основі цього тесту визначається чиста та мішана гетероскедастичність. За цим тестом необхідно знайти залежність між модулем залишків та кожною пояснювальною змінною:

.

У цій моделі перевіряється достовірність оцінок параметрів та

Побудуємо прості економетричні моделі модуля залишків залежно від кожної пояснювальної змінної:

5,586 – 0,046x₁;

(1,888) (–1,204)

4,049 – 0,071x₂;

(2,249) (–1,226)

7,051 – 0,041x₃.

(1,424) (–1,012)

Перевіримо статистичну значущість оцінок параметрів кожної з цих моделей, застосувавши t-статистику.

У дужках під оцінками параметрів моделей приведені фактичні значення t-критеріїв. Табличне значення цього критерію за рівня значущості  = 0,05 і ступеня свободи n – m = 18 дорівнює:

t_{(0,05) крит} = 2,10.

Порівнюючи фактичні значення t-критеріїв з табличним, робимо висновок, що в другому рівнянні оцінка параметра a₀ є статистично значущою. Отже, можна дійти висновку про наявність мішаної гетероскедастичності, яка викликається зміною тих пояснювальних змінних, які впливають на залежну змінну, але не включені до моделі.

Щоб оцінити параметри моделі узагальненим методом найменших квадратів, необхідно сформувати матрицю S.

Побудова матриці P, S, P^–1, S^–1. Оскільки ми маємо справу з мішаною гетероскедастичністю, то використовуємо третю гіпотезу щодо визначення _і:

.

Для розрахунку використаємо модель:

бо в цій моделі оцінка параметра статистично значуща.

Підставивши в цю модель фактичні значення пояснювальної змінної Х₂, дістанемо розрахункові залишки за модулем та квадрати цих залишків:

Значення вектора abs() є діагональними елементами матриціP^–1, а значення вектора (abs(— діагональними елементами матриціS^–1.

Запишемо матрицю S, діагональні елементи якої визначаються за такою формулою: , де

Оцінювання параметрів моделі методом Ейткена за допомогою матриці S^–1. Оператор оцінювання запишеться у такому вигляді:

Прогноз залежної змінної. Точковий прогноз за наявності гетероскедастичності має такий вигляд:

,

де — вектор оцінок параметрів моделі, здобутих методом Ейткена;

—останній діагональний елемент матриці Р^–1 (1,409299);

—останній елемент залишків, здобутих методом 1МНК (0,624327).

Запишемо вектор прогнозованих пояснювальних змінних:

.

Тоді прогнозне значення прибутку буде таке: .

Для того щоб знайти інтервальний прогноз прибутку, необхідно обчислити стандартну похибку прогнозу. Вона визначається за формулою:

,

,

,

.

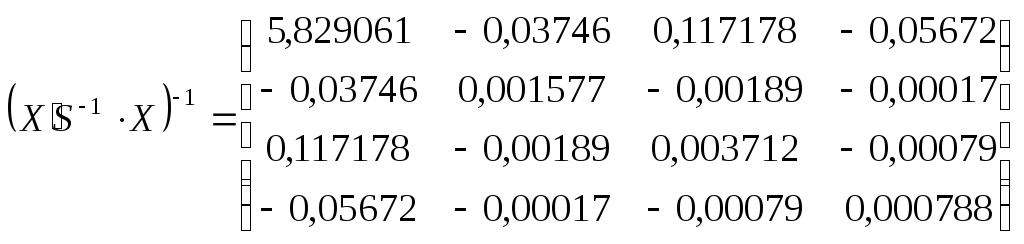Перейдемо від стандартної похибки прогнозу до граничної, яка подається у такому вигляді:

,

Додавши похибку до точкового прогнозу, дістанемо максимально можливе значення залежної змінної на перспективу, а віднявши — мінімальне значення: