Гетероскедастичність

Припущення, які було зроблено під час оцінювання параметрів моделі 1МНК, на практиці можуть порушуватися.

У розд. 6 було розглянуто проблему мультиколінеарності, яка пов’язана з порушенням четвертої умови.

Рік	Заощадження	Дохід	Рік	Заощадження	Дохід
1	0,36	8,8	10	0,59	15,5
2	0,2	9,4	11	0,90	16,7
3	0,08	10,0	12	0,95	17,7
4	0,20	10,6	13	0,82	18,6
5	0,10	11,0	14	1,04	19,7
6	0,12	11,9	15	1,53	21,1
7	0,41	12,7	16	1,94	22,8
8	0,50	13,5	17	1,75	23,9
9	0,43	14,3	18	1,99	25,2

Тепер розглянемо особливості економетричного моделювання, коли порушується умова (4.3), згідно з якою припускається, що відхилення мають такий розподіл імовірностей, який зберігається для всіх спостережень. Тоді дисперсія залишків лишається незмінною для кожного спостереження.

Означення 7.1. Якщо дисперсія залишків стала для кожного спостереження, тобто , то ця її властивість називаєтьсягомоскедастичністю.

Часто у практичних дослідженнях явище гомоскедастичності залишків порушується. Наприклад, будуючи економетричну модель, що характеризує залежність між заощадженнями і доходами населення на підставі теоретичної та практичної інформації, можна висунути гіпотезу, що дисперсія залишків за окремими групами населення змінюватиметься і буде пропорційною до середнього доходу цієї групи. Коли розглядати економетричну модель, що характеризує залежність між депозитними вкладами і розміром прибутку клієнтів банку або між витратами на харчування і доходом на одного члена сім’ї, витратами на харчування і загальними витратами, то також можна припустити, що дисперсія залишків для окремих груп спостережень змінюватиметься. У цих залежностях пояснювальна змінна може різко змінюватись, а динаміка залежної змінної буде досить помірною, не адекватною до зміни пояснювальної змінної. Це і приводить до зміни дисперсії залишків кожного спостереження або ж груп спостережень.Означення 7.2. Якщо дисперсія залишків змінюється для кожного спостереження або групи спостережень, тобто , то це явище називаєтьсягетероскедастичністю.

7.2. Наслідки гетероскедастичності

За наявності гетероскедастичності оцінки параметрів, отримані 1МНК, як правило, залишаються незміщеними, обґрунтованими, але неефективними.

Нагадаємо, що дисперсія оцінок параметрів простої лінійної моделі визначається так:

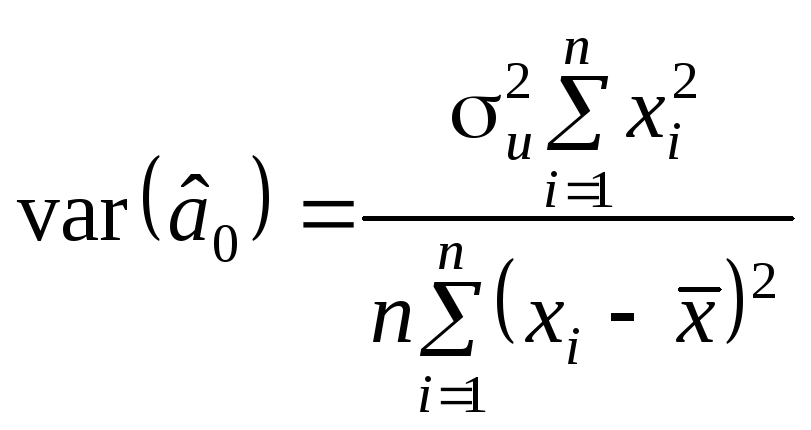; (7.1)

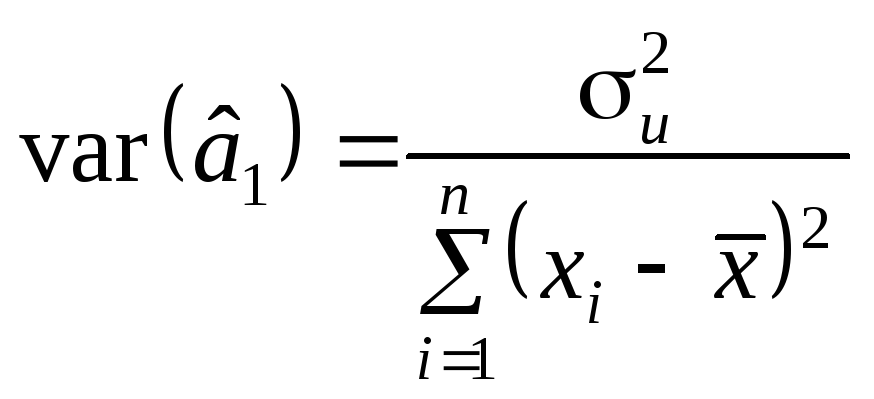. (7.2)

Рік			Рік
1	0,041	0,114	10	0,038	0,065
2	0,022	0,106	11	0,054	0,060
3	0,008	0,100	12	0,054	0,056
4	0,019	0,094	13	0,044	0,054
5	0,009	0,091	14	0,053	0,051
6	0,010	0,084	15	0,073	0,047
7	0,032	0,079	16	0,085	0,044
8	0,037	0,074	17	0,073	0,042
9	0,030	0,070	18	0,079	0,040

У цих співвідношеннях дисперсія залишків є сталою, тому вона винесена за знак суми. За гетероскедастичності дисперсія буде змінюватись через зростаючий розкид значень залишків, тобто вона зростатиме. Це означає, щобуде зростати дисперсія оцінок параметрів моделі, яка приводить до збільшення їхніх стандартних похибок.

Дисперсія оцінки у разі гетероскедастичності запишеться так:

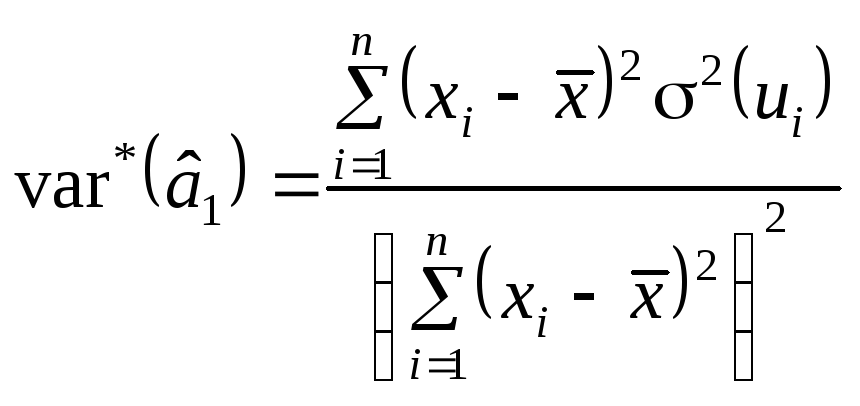. (7.3)

Порівнюючи обидва співвідношення дисперсій оцінок , бачимо, що, тобто дисперсія оцінки параметраза гетероскедастичності більша, ніж дисперсія цієї оцінки за гомоскедастичності.

Звідси інтервали довіри оцінок параметрів моделі також будуть більшими. Як наслідок, F та t-критерії дають неточні результати.

Таким чином, якщо не звертати увагу на гетероскедастичність і використовувати звичайні процедури перевірки гіпотез, то висновки будуть неправильними, тобто потенційно гетероскедастичність є серйозною проблемою.

Пояснимо сутність побудови моделі 1МНК за наявності гетероскедастичності.

Припустимо, що дисперсія залишків змінюється пропорційно до величини , деx_ij — i-те значення j-ї пояснювальної змінної, яка може викликати гетероскедастичність.

Тоді, щоб усунути гетероскедастичність, можна перетворити вихідну інформацію, поділивши кожну зі змінних на x_ij і до цієї інформації застосувати 1МНК.

Економетрична модель матиме вигляд:

(7.4)

У результаті для оцінювання параметрів можна застосувати 1МНК. Зауважимо, що параметри а₀ і а₁ помінялися ролями. Віль­ним членом моделі замість а₀ стала оцінка параметра а₁.

Приклад 7.1. побудуємо економетричну модель, що характеризує залежність між заощадженнями та доходом населення, млрд ф. ст. (табл. 7.1).

Таблиця 7.1

Скориставшись оператором оцінювання 1МНК

дістанемо = –1,081;= 0,1178.

Економетрична модель має такий вигляд:

Коефіцієнт детермінації для цієї моделі= 0,918, а це означає, що варіація заощадженьY на 91,8 % визначається варіацією доходів населення.

На перший погляд, результат наводить на думку, що специфікація моделі не містить похибки.

Але логічно висунути гіпотезу, що відхилення заощаджень можуть бути пропорційними до доходу, тобто для цієї моделі досить ймовірне існування гетероскедастичності залишків.

Отже, вихідну інформацію перетворимо, поділивши обидві змінні на дохід X (табл. 7.2):

Нове рівняння зв’язку згідно з даними табл. 7.2 має такий вигляд:

У результаті перетворення вихідних даних практично повністю змінилася специфікація моделі. Оскільки , то цей зв’язок нелінійний. По-друге,характеризує відносний показник — рівень заощаджень, який припадає на одиницю доходу.

Виконавши цю процедуру, дістанемо таке: спостереження з меншими значеннямимають відносно більшу питому вагу при оцінюванні параметрів моделі, ніж у першому варіанті.

З наведеного прикладу бачимо, що явище гетероскедастичності не впливатиме на оцінки параметрів 1МНК, якщо певним чином перетворити вихідну інформацію. Згідно з цим, якщо економетрична модель має лише дві змінні, то це можна зробити так, як у прикладі 7.1.

Це перетворення значно ускладнюється, якщо будується економетрична модель з багатьма змінними. У такому разі потрібно з’ясувати зміст гіпотези, згідно з якою , делишається невідомим параметром, а— відома симетрична додат­но визначена матриця.