MATEMATIKA_EKZAMEN / ЛЕКЦИИ2 / Тема 1. Множества. Логика

Тема 1. Множества. Логика.

Элемент и множество, принадлежность. Пустое множество. Равенство множеств. Задание множеств. Конечные и бесконечные множества. Подмножество, отношение включения. Операции объединения, пересечения и разности над множествами. Свойства операций. Пары, равенство пар. Декартово произведение двух множеств. Высказывания, истинность и ложность высказываний. Импликации, эквивалентные высказывания. Кванторы существования и всеобщности.

Множество -- неопределяемое понятие. Запись означает, что элемент принадлежит множеству . Отношение принадлежности также неопределяемо. Запись значит, что элемент не принадлежит множеству . Среди всех множеств есть пустое множество ∅, которое не содержит ни одного элемента. Два множества равны, если и только, если они состоят из одних и тех же элементов (аксиома).

Множество, состоящее из элементов , записывается как . Различают конечные и бесконечные множества. Если множество бесконечно, то очень часто его задают следующим образом:

Здесь -- некоторое универсальное множество, из которого и отбираются элементы. Например, -- множество всех действительных чисел, синус которых равен нулю. Это множество совпадает с множеством {0,± π ,± 2π ,± 3π ,… }.

Объединением множеств и называется множество , состоящее из всех элементов, принадлежащих либо , либо . Пересечением множеств A и B называется множество A∩B, состоящее из всех элементов, принадлежащих как , так и . Разностью множеств и называется множество , состоящее из всех элементов, принадлежащих , но не принадлежащих .

Множество называется подмножеством множества , если всякий элемент из B принадлежит также и 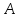. Записывается это отношение так: или . Здесь употреблен символ нестрого включения. Если мы хотим выразить, что и 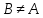, то пишем (строгое включение).

Пара это новый математический объект. Считаем, что в том и только том случае, когда одновременно и .