
- •Тема 12 Неопределенный интеграл
- •Первообразная и неопределенный интеграл
- •Простейшие свойства неопределенного интеграла.
- •Замена переменной в неопределённом интеграле
- •Интегрирование по частям в неопределённом интеграле
- •Интегрирование иррациональных выражений
- •Интегрирование тригонометрических выражений
- •Тема 13 определенный интеграл
- •Определение определенного интеграла
- •Свойства определённого интеграла
- •Формула Ньютона-Лейбница
- •Замена переменной и интегрирование по частям в определённом интеграле
- •Несобственные интегралы
- •Тема14. Приложение определённого интеграла
- •Длина дуги
Свойства определённого интеграла
Монотонность
интеграла.Если для всех
для всех и
и ,
то
,
то .
.
Действительно,
в этом случае
 и переходя к пределу
и переходя к пределу в этом неравенстве (см. раздел «Введение
в анализ»), получаем искомое соотношение
между интегралами.
в этом неравенстве (см. раздел «Введение
в анализ»), получаем искомое соотношение
между интегралами.
Как следующее свойство отметим одно простое равенство, вытекающее из определения определенного интеграла:

Оценка
интеграла.Если на отрезке
на отрезке и
и ,
то
,
то

Действительно,
 Здесь мы последовательно применили
монотонность интеграла, его линейность
и равенство (1). Аналогично доказывается
первое из неравенств в (2).
Здесь мы последовательно применили
монотонность интеграла, его линейность
и равенство (1). Аналогично доказывается
первое из неравенств в (2).
Например,
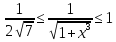 на отрезке
на отрезке ,
что следует из монотонности функции
,
что следует из монотонности функции а значит и функции
а значит и функции . Отсюда,
. Отсюда,

Теорема о среднем. Если функция непрерывна на отрезке
непрерывна на отрезке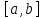 ,
то найдётся точка
,
то найдётся точка такая,
что
такая,
что

Величина
 называется интегральным средним функции
называется интегральным средним функции на отрезке
на отрезке .
.
Доказательство.
По теореме Вейерштрасса, функция
 на отрезке
на отрезке достигает своего наибольшего значения
достигает своего наибольшего значения )
и наименьшего значения
)
и наименьшего значения .
Здесь
.
Здесь -- некоторые точки отрезка
-- некоторые точки отрезка .
Применяя оценку интеграла (2), выводим
.
Применяя оценку интеграла (2), выводим

Интегральное
среднее оказывается промежуточным
значением между наименьшим и наибольшим
значениями. Применим теорему Больцано-Коши
о промежуточном значении к непрерывной
функции
 и найдем точку
и найдем точку между
между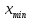 и
и (значит
(значит )
такую, что
)
такую, что .□
.□
Пример. Пусть

Тогда
интегральное среднее функции (4) на
отрезке
 равно
равно

Однако
точки
 такой, что
такой, что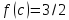 нет. Причина этого – разрыв функции
нет. Причина этого – разрыв функции в точке 1.
в точке 1.
Формула Ньютона-Лейбница
Интеграл
вида
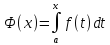 называют интегралом с переменным
верхним пределом.
называют интегралом с переменным
верхним пределом.
Теорема.
Пусть
 непрерывна на отрезке
непрерывна на отрезке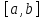 .
Тогда
.
Тогда есть первообразная функции
есть первообразная функции
 :
:

для любого
 .
.
Доказательство.
Пусть
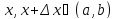 .
Тогда по теореме о среднем
.
Тогда по теореме о среднем

для некоторой
точки Следовательно,
Следовательно,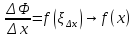 при
при ,
ибо в этом случае
,
ибо в этом случае ,
а функция
,
а функция непрерывна.□
непрерывна.□
Формула
Ньютона-Лейбница. Пусть
 -- первообразная функции
-- первообразная функции .
Тогда
.
Тогда
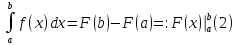
Доказательство.
Для функции
 имеем в распоряжении две первообразных
имеем в распоряжении две первообразных и
и . По теореме о первообразных (см.§
1 )найдется константа
. По теореме о первообразных (см.§
1 )найдется константа такая, что
такая, что

Подставим
в соотношение (3) вместо
 сначала
сначала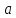 и получим
и получим ,
а затем подставим
,
а затем подставим в (3) – получим
в (3) – получим

что и требовалось доказать.
Пример.
 (см. пример вычисления площади в начале§6).
(см. пример вычисления площади в начале§6).
Замена переменной и интегрирование по частям в определённом интеграле
Замена
переменной. Пусть -- дифференцируемое отображениеcнепрерывной производной и такое, что
-- дифференцируемое отображениеcнепрерывной производной и такое, что ,
а
,
а -- непрерывная функция, заданная на
отрезке
-- непрерывная функция, заданная на
отрезке .
Тогда
.
Тогда

Доказательство.
Пусть
 -- первообразная функции
-- первообразная функции .
Тогда по формуле замена переменной в
неопределенном интеграле функция
.
Тогда по формуле замена переменной в
неопределенном интеграле функция есть первообразная функции
есть первообразная функции .
Применим формулу Ньютона-Лейбница
дважды:
.
Применим формулу Ньютона-Лейбница
дважды:

-- что и требовалось доказать. □
Пример 1.Вычислим площадь верхнего полукруга радиусаR.
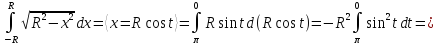

Интегрирование по частям. Пусть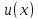 и
и -- дифференцируемые функции на отрезке
-- дифференцируемые функции на отрезке .
Тогда
.
Тогда

Доказательство.
Соотношение
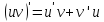 проинтегрируем от
проинтегрируем от до
до bполучим
bполучим что эквивалентно (2).
что эквивалентно (2).
Пример 2.Вычислим
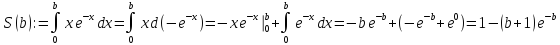
Заметим,
что
 при условии
при условии
Несобственные интегралы
Пусть
функция
 задана на полуинтервале
задана на полуинтервале ,
где
,
где ,
а величина
,
а величина может быть как конечным числом, так и
может быть как конечным числом, так и .
Предположим, что
.
Предположим, что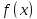 интегрируема на любом отрезке
интегрируема на любом отрезке ,
, .
Полагаем по определению
.
Полагаем по определению
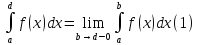
и называем это число несобственным интегралом. В случае, когда предел (1) существует, то говорим, что соответствующий интеграл сходится; в противном случае будем говорить, что онрасходится.
Несобственный интеграл (1) применяется в двух типичных ситуациях.
1) Пусть
 . Тогда
. Тогда
2) Пусть d∈ℝи функция неограничена на полуинтервале
неограничена на полуинтервале .
.
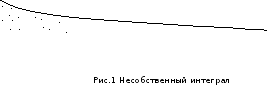
Если
 на полуинтервале
на полуинтервале ,
то несобственный интеграл равен площади
неограниченной фигуры -- криволинейной
трапеции, ограниченной сверху графиком
функции
,
то несобственный интеграл равен площади
неограниченной фигуры -- криволинейной
трапеции, ограниченной сверху графиком
функции ,
снизу – осью Ох и слева – вертикальной
прямой
,
снизу – осью Ох и слева – вертикальной
прямой (см. рис. 1)
(см. рис. 1)
Отметим,
что если функция на самом деле интегрируема на отрезке
на самом деле интегрируема на отрезке (это означает, в частности, что
(это означает, в частности, что ), то коллизии обозначений не возникает
-- несобственный интеграл в смысле (1)
будет равен определенному интегралу
функции
), то коллизии обозначений не возникает
-- несобственный интеграл в смысле (1)
будет равен определенному интегралу
функции на отрезке
на отрезке .
.
Аналогично
определяется несобственный интеграл
для функций, определенных на полуинтервале
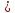 ,
где
,
где и
и :
:

В примере
§8 мы фактически
вычислили несобственный интеграл .
.
Формула
Ньютона-Лейбница для несобственных
интегралов. Пусть -- первообразная непрерывной функции
-- первообразная непрерывной функции на интервале (c,d). Предположим, что
существуют пределы
на интервале (c,d). Предположим, что
существуют пределы

Тогда
несобственный интеграл
 сходится, причём
сходится, причём
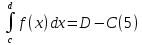
Равенство (5) вытекает из формулы Ньютона-Лейбница для обычных интегралов и соотношений (4).
Пример. Вычислим

Предложение об "эталонных" интегралах . Пусть a>0.
Интеграл
 сходится тогда и только тогда, когда
p>1.
сходится тогда и только тогда, когда
p>1.Интеграл
 сходится тогда и только тогда, когдаp<1.
сходится тогда и только тогда, когдаp<1.
Доказательство.
1. Если ,
то первообразная
,
то первообразная подинтегральной функции
подинтегральной функции имеет конечный предел 0 при
имеет конечный предел 0 при .
По формуле Ньютона-Лейбница для
несобственных интегралов, получаем,
что интеграл
.
По формуле Ньютона-Лейбница для
несобственных интегралов, получаем,
что интеграл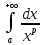 сходится и равен
сходится и равен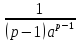 .
.
Если
 ,
то первообразной подинтегральной
функции служит
,
то первообразной подинтегральной
функции служит , который не имеет конечного предела на
, который не имеет конечного предела на .
Для
.
Для то же самое можно сказать о первообразной
то же самое можно сказать о первообразной .
.
Аналогично, прямыми вычислениями доказывает второе утверждение.
Примеры
1. Интеграл сходится,
так как здесь
сходится,
так как здесь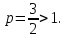
2. Докажем,
что интегралы
 и
и сходятся и вычислим их. Имеем
сходятся и вычислим их. Имеем

Интеграл
 также сходится, ибо занесение под знак
дифференциала
также сходится, ибо занесение под знак
дифференциала и замена
и замена превращают его в интеграл
превращают его в интеграл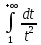 ,
который сходится согласно предложению
об эталонных интегралах и равен 1.
,
который сходится согласно предложению
об эталонных интегралах и равен 1.
Интегралы
 и
и расходятся, так как такая же замена
приводит их к несобственным эталонным
интегралам
расходятся, так как такая же замена
приводит их к несобственным эталонным
интегралам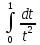 и
и ,
с
,
с
