
- •Тема 12 Неопределенный интеграл
- •Первообразная и неопределенный интеграл
- •Простейшие свойства неопределенного интеграла.
- •Замена переменной в неопределённом интеграле
- •Интегрирование по частям в неопределённом интеграле
- •Интегрирование иррациональных выражений
- •Интегрирование тригонометрических выражений
- •Тема 13 определенный интеграл
- •Определение определенного интеграла
- •Свойства определённого интеграла
- •Формула Ньютона-Лейбница
- •Замена переменной и интегрирование по частям в определённом интеграле
- •Несобственные интегралы
- •Тема14. Приложение определённого интеграла
- •Длина дуги
Интегрирование иррациональных выражений
Далее
 -- рациональная функция одной или
нескольких переменных.
-- рациональная функция одной или
нескольких переменных.
Интегралы
вида
 ,
где m/n,...,r/s -- рациональные числа с общим
знаменателем k, сводятся к интегралу
от рациональной функции заменой
,
где m/n,...,r/s -- рациональные числа с общим
знаменателем k, сводятся к интегралу
от рациональной функции заменой

Тогда
 суть рациональные выражения, следовательно,
после подстановки, получается интеграл
от рациональной дроби:
суть рациональные выражения, следовательно,
после подстановки, получается интеграл
от рациональной дроби:

Вычислив
этот интеграл (см. пар. 4) и сделав обратную
замену
 ,
получим ответ.
,
получим ответ.
Аналогично, интегралы вида

где ad-bc≠ 0, аkимеет тот же смысл как и выше, сводятся к интегралам от рациональной дроби заменой

Примеры. А. Вычислим интеграл

Б. Вычислим интеграл

Более простой метод интегрирования (но требующий догадки) этой же функции таков:

Интегрирование тригонометрических выражений
Интегралы
вида
 сводятся к интегралам от рациональной
функции универсальной заменой
сводятся к интегралам от рациональной
функции универсальной заменой

Тогда

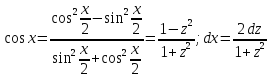
поэтому получаем интеграл от рационального выражения
В частных
случаях R(sin x) cos x
dx,R(cosx)sinxdxиR(sin2x, cos2x,
tg x, ctg x) dx лучше пользоваться заменами соответственно.
соответственно.
Примеры. А.

Б.
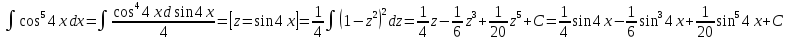
Задачи
Вычислить интеграл

Вычислить а)
 б)
б)
Найти а)
 ;
б)
;
б)
Вычислить

Вычислить

Вычислить
Вычислить а)
 ;
б)
;
б)
 ;
в)
;
в)
 ;
г)
;
г)

Тема 13 определенный интеграл
Определение определенного интеграла
Пусть
функция
 определена на отрезке
определена на отрезке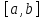 и неотрицательна. Фигура, заданная
неравенствами
и неотрицательна. Фигура, заданная
неравенствами называется криволинейной трапецией
(см. рис. 1). Вычислим площадь криволинейной
трапеции. Идея вычисления состоит в
том, чтобы нарезать эту трапецию на
узенькие вертикальные полоски, площадь
каждой полоски считать как площадь
прямоугольника, а затем сложить
получившиеся результаты. Мы получим
приближенный ответ. Для получения
точного ответа надо брать полоски все
уже и уже и перейти к пределу, когда
максимальная ширина полоски стремится
к нулю. Вычислим таким образом площадь
под экспонентой
называется криволинейной трапецией
(см. рис. 1). Вычислим площадь криволинейной
трапеции. Идея вычисления состоит в
том, чтобы нарезать эту трапецию на
узенькие вертикальные полоски, площадь
каждой полоски считать как площадь
прямоугольника, а затем сложить
получившиеся результаты. Мы получим
приближенный ответ. Для получения
точного ответа надо брать полоски все
уже и уже и перейти к пределу, когда
максимальная ширина полоски стремится
к нулю. Вычислим таким образом площадь
под экспонентой ,
если
,
если .
Возьмём равномерное разбиение отрезка
[a,b]:
.
Возьмём равномерное разбиение отрезка
[a,b]:

 ;
;
Тогда


Здесь
использована формула суммы геометрической
прогрессии, а также эквивалентность
бесконечно малых
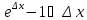 при
при .
Так как функция exнепрерывна, то
доказано, что S=eb-ea.
.
Так как функция exнепрерывна, то
доказано, что S=eb-ea.
Перейдем
к точным определениям. Разбиением
отрезка
 называется семейство точек
называется семейство точек таких, что
таких, что

Параметром
разбиения (обозначим его
 )
называется наибольшее из приращений
)
называется наибольшее из приращений когда индекс
когда индекс пробегает от 1 до n. Пусть
пробегает от 1 до n. Пусть - функция, определенная на отрезке
- функция, определенная на отрезке и
и - какие-либо (отмеченные) точки из отрезков
- какие-либо (отмеченные) точки из отрезков .
Тогда
.
Тогда

называется интегральной суммой.
Определение.Определённым интегралом функции на отрезке
на отрезке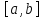 называется предел интегральных сумм,
если параметр разбиения стремиться к
нулю:
называется предел интегральных сумм,
если параметр разбиения стремиться к
нулю:

Если
 ,
то по определению полагаем
,
то по определению полагаем .
Если же
.
Если же ,
то считаем по определению
,
то считаем по определению

Функция
 называется подинтегральной,
называется подинтегральной, называется подинтегральным выражением.
Число
называется подинтегральным выражением.
Число называется нижним пределом интегрирования,
а
называется нижним пределом интегрирования,
а – верхним пределом интегрирования.
– верхним пределом интегрирования.
Так как
предел не всегда существует, то и
определенный интеграл на отрезке
 существует не от любой функции.
Необходимым условием существования
интеграла является ограниченность
функции
существует не от любой функции.
Необходимым условием существования
интеграла является ограниченность
функции на отрезке
на отрезке .Действительно, если функция
.Действительно, если функция неограничена, например, сверху, то при
любом разбиении, каков бы ни был малый
его параметр, найдутся отмеченные точки
неограничена, например, сверху, то при
любом разбиении, каков бы ни был малый
его параметр, найдутся отмеченные точки такие, что интегральная сумма (2) больше
чем любая наперед заданная величина.
Следовательно, конечного предела
интегральные суммы иметь не могут.
такие, что интегральная сумма (2) больше
чем любая наперед заданная величина.
Следовательно, конечного предела
интегральные суммы иметь не могут.
Функцию
 ,
заданную на отрезке
,
заданную на отрезке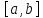 ,
для которой предел (3) существует, назовем
интегрируемой (по Риману) на этом отрезке.
Сумма интегрируемых функций есть
интегрируемая функция и произведение
интегрируемой функции на число есть
также интегрируемая функция. Более
того, отображение, сопоставляющее
функции
,
для которой предел (3) существует, назовем
интегрируемой (по Риману) на этом отрезке.
Сумма интегрируемых функций есть
интегрируемая функция и произведение
интегрируемой функции на число есть
также интегрируемая функция. Более
того, отображение, сопоставляющее
функции интеграл
интеграл линейно. Это значит, что если
линейно. Это значит, что если интегрируемы, то для любых чисел
интегрируемы, то для любых чисел линейная комбинация
линейная комбинация также интегрируема на отрезке
также интегрируема на отрезке и
и

Заметим,
что из определения интеграла, у которого
нижний предел больше или равен верхнему
вытекает, что равенство (4) справедливо
вне зависимости от расположения точек
 и
и на числовой прямой.
на числовой прямой.
На
существование и на значение определенного
интеграла не влияет изменение значения
функции
 в конечном числе точек.
в конечном числе точек.
Адитивность
интеграла. Пусть
 .
Тогда функция
.
Тогда функция интегрируема на отрезке
интегрируема на отрезке в том и только том случае, когда она
интегрируема на
в том и только том случае, когда она
интегрируема на и на
и на .
В этом случае
.
В этом случае

Если точки
 расположены произвольно на числовой
прямой и каждый из интегралов в (5)
существует, то равенство (5) имеет место.
расположены произвольно на числовой
прямой и каждый из интегралов в (5)
существует, то равенство (5) имеет место.
Доказательство.
Если
 ,
то интегральную сумму на отрезке
,
то интегральную сумму на отрезке можно разбить на две интегральные суммы
– на отрезке
можно разбить на две интегральные суммы
– на отрезке и на отрезке
и на отрезке .
Формула (5) вытекает по существу из
свойства: предел суммы равен сумме
пределов.
.
Формула (5) вытекает по существу из
свойства: предел суммы равен сумме
пределов.
Рассмотрим
случай
 расположения точек
расположения точек .
Тогда по условию и доказанному выше
имеет место равенство
.
Тогда по условию и доказанному выше
имеет место равенство . Перенося
. Перенося в левую часть и заменяя
в левую часть и заменяя на
на получаем
получаем ,
что совпадает с (5). Аналогично разбираются
другие случаи расположения точек
,
что совпадает с (5). Аналогично разбираются
другие случаи расположения точек .□
.□
Теорема 2. Кусочно-непрерывная функция интегрируема на любом отрезке.
