
- •Тема 12 Неопределенный интеграл
- •Первообразная и неопределенный интеграл
- •Простейшие свойства неопределенного интеграла.
- •Замена переменной в неопределённом интеграле
- •Интегрирование по частям в неопределённом интеграле
- •Интегрирование иррациональных выражений
- •Интегрирование тригонометрических выражений
- •Тема 13 определенный интеграл
- •Определение определенного интеграла
- •Свойства определённого интеграла
- •Формула Ньютона-Лейбница
- •Замена переменной и интегрирование по частям в определённом интеграле
- •Несобственные интегралы
- •Тема14. Приложение определённого интеграла
- •Длина дуги
Тема 12 Неопределенный интеграл
Первообразная и неопределенный интеграл
Решаем дифференциальное уравнение

на интервале
 .
Так как
.
Так как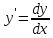 ,
то уравнение (1) можно переписать в
дифференциалах:
,
то уравнение (1) можно переписать в
дифференциалах:
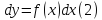
Любое
решение такого уравнения называется
первообразной функции
 .
По-другому, функция
.
По-другому, функция называетсяпервообразной функции
называетсяпервообразной функции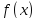 на интервале
на интервале ,
если
,
если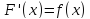 для всех
для всех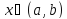 .
Случаи
.
Случаи и/или
и/или не исключаются. Ясно, что если
не исключаются. Ясно, что если первообразная, то и
первообразная, то и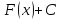 также первообразная. Наша задача –
найти все решения уравнения (1). Функция
двух переменных
также первообразная. Наша задача –
найти все решения уравнения (1). Функция
двух переменных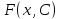 называется общим решением уравнения
(1) или неопределенным интегралом функции
называется общим решением уравнения
(1) или неопределенным интегралом функции ,
если при подстановке вместо
,
если при подстановке вместо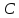 любого числа получаем частное решение
уравнения (1) и любое частное решение
уравнения (1) получается таким образом.
любого числа получаем частное решение
уравнения (1) и любое частное решение
уравнения (1) получается таким образом.
Неопределённый
интеграл обозначается
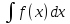 .
Функция
.
Функция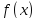 называется подинтегральной, дифференциал
называется подинтегральной, дифференциал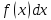 называется подинтегральным выражением,
а
называется подинтегральным выражением,
а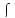 -- знак интеграла (растянутая латинская
букваS, первая буква словаSum– сумма). Возникает
вопрос о существовании первообразной
и неопределенного интеграла. В разделе
«Определенный интеграл»,§Формула Ньютона-Лейбница будет доказано,
что первообразная непрерывной функции
всегда существует.
-- знак интеграла (растянутая латинская
букваS, первая буква словаSum– сумма). Возникает
вопрос о существовании первообразной
и неопределенного интеграла. В разделе
«Определенный интеграл»,§Формула Ньютона-Лейбница будет доказано,
что первообразная непрерывной функции
всегда существует.
Лемма.
Пусть
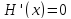 тождественно для всех
тождественно для всех .
Тогда
.
Тогда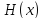 -- константа на этом интервале.
-- константа на этом интервале.
Доказательство.
Обозначим
 для какой-либо точки
для какой-либо точки .
Возьмём произвольную точку
.
Возьмём произвольную точку и к разности
и к разности применим теорему Лагранжа:
применим теорему Лагранжа: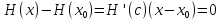 для некоторой точки
для некоторой точки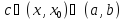 .
Отсюда
.
Отсюда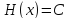 и лемма доказана.□
и лемма доказана.□
Теорема о первообразных. Две первообразных одной и той же функции, определенной на интервале, отличаются на константу.
Доказательство.
Пусть
 и
и -- первообразные функции
-- первообразные функции .
Тогда
.
Тогда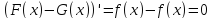 откуда, по лемме
откуда, по лемме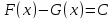 -- константа. Следовательно,
-- константа. Следовательно,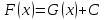 .□
.□
Следствие.
Если
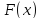 -- первообразная функции
-- первообразная функции ,
то
,
то ,
где C пробегает множество действительных
чисел.
,
где C пробегает множество действительных
чисел.
Простейшие свойства неопределенного интеграла.
1. Интеграл от суммы равен сумме интегралов:

2. Константу можно выносить за знак интеграла:
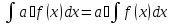
3. Производная от интеграла равна подинтегральной функции.
4. Дифференциал от интеграла равен подинтегральному выражению.
5. (Линейная
замена переменных) Если
 ,
то
,
то (здесь
(здесь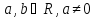 ).
).
Таблица основных интегралов
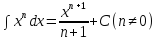
В частности,

Для
исключительного случая
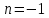 имеем:
имеем:

Далее
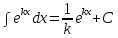
|
f(x) |
|
|
|
|
|
|
|
|
|
|
F(x) |
|
|
|
|
|
|
|
|
|
|
f(x) |
|
|
|
|
|
|
|
F(x) |
|
|
|
|
|
|
Задачи
Найти а)
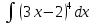 ;
б)
;
б)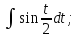 в)
в) ;
г)
;
г)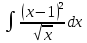
Найти а)
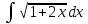
Решить дифференциальное уравнение
 с условием
с условием
Решить дифференциальное уравнение
 с условиями
с условиями
Решить дифференциальное уравнение

Замена переменной в неопределённом интеграле
Определение
неопределенного интеграла распространим
на более общий случай: полагаем по
определению
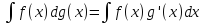 .
Таким образом, например
.
Таким образом, например
 .
.
Теорема.Пусть -- дифференцируемая функция. Тогда
-- дифференцируемая функция. Тогда

Доказательство.
Пусть
 .
Тогда
.
Тогда

что и требовалось доказать.□
В частном
случае, когда
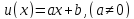 получаем линейную замену переменных
(см. свойство 5,§1).
Применение формулы (1) "слева на право"
и будет означать замену переменной .
Применение формулы (1) в обратном
направлении, "справа налево"
называется занесением под знак
дифференциала.
получаем линейную замену переменных
(см. свойство 5,§1).
Применение формулы (1) "слева на право"
и будет означать замену переменной .
Применение формулы (1) в обратном
направлении, "справа налево"
называется занесением под знак
дифференциала.
Примеры.А.

В.

Г.
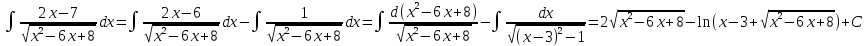
Интегрирование по частям в неопределённом интеграле
Теорема.
Для дифференцируемых функций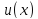 и
и имеет место соотношение
имеет место соотношение

Доказательство.
Интегрируя левую и правую часть формулы
 ,
получаем:
,
получаем:
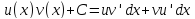
Так как по
определению
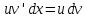 и
и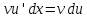 ,
то формула (1) следует.□
,
то формула (1) следует.□
Пример.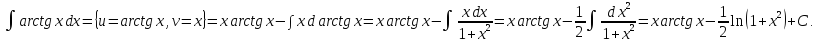
Метод интегрирования функций вида
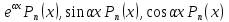 .
.
Здесь и
далее
 – многочлен степени n. Метод интегрирования
состоит в занесении экспоненты или
гармоники под знак дифференциала, а
затем применяется формула интегрирования
по частям. Повторяем эту процедуру n
раз.
– многочлен степени n. Метод интегрирования
состоит в занесении экспоненты или
гармоники под знак дифференциала, а
затем применяется формула интегрирования
по частям. Повторяем эту процедуру n
раз.
Пример.

Метод интегрирования функций вида
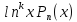 :
:
Для интегрирования таких функций заносим многочлен под знак дифференциала и применяем формулу интегрирования по частям. Процедуру повторяем k раз.
Пример.
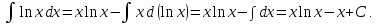

Задачи
Вычислить, применяя занесение под знак дифференциала а)
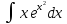 ;
б)
;
б)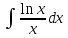 ;
в)
;
в)
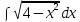 (применить
подстановку
(применить
подстановку
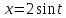 )
)Вычислить, применяя формулу интегрирования по частям а)
 б)
б)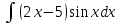 ;
в)
;
в)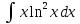 ;
г)
;
г)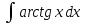
* Вычислить

Интегрирование рациональных дробей
Рациональной
дробью называется функция вида
 ,
где
,
где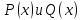 – многочлены. Если
– многочлены. Если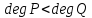 ,
то рациональную дробь
,
то рациональную дробь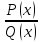 называют правильной. В противном случае
ее называют неправильной.
называют правильной. В противном случае
ее называют неправильной.
Следующие рациональные дроби называют простейшими
(1 тип)
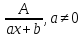 ,
,
(2 тип)
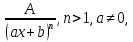
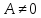
(3 тип)

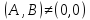
(4 тип)
 ,
,
Теорема 1. Любую дробь можно разложить в сумму многочлена и правильной рациональной дроби.
Доказательство.
Пусть
 – неправильная рациональная дробь.
Поделим числитель на знаменатель с
остатком:
– неправильная рациональная дробь.
Поделим числитель на знаменатель с
остатком: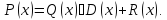 Здесь
Здесь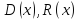 --
многочлены, причем
--
многочлены, причем Тогда
Тогда
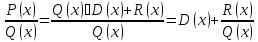
Дробь
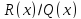 правильная в силу неравенства
правильная в силу неравенства .□
.□
Теорема 2.Любую правильную рациональную дробь можно разложить в сумму простейших.
Примеры.А. Разложим в сумму простейших
в сумму простейших

Отсюда
следует, что
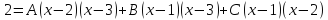 .
Подставляя в это соотношение
.
Подставляя в это соотношение находим сразу
находим сразу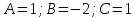 .
Итак
.
Итак


 (λ ≠ 0)
(λ ≠ 0)

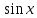

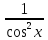


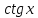
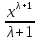
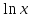
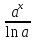
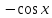

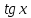










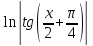
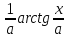
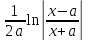 (высокий
логарифм)
(высокий
логарифм)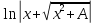 (длинный
логарифм)
(длинный
логарифм)