3. Матричное исчисление

1. Понятие матрицы

Матрицей размера или–матрицей называется прямоугольная таблица вида⋮

мыслимая как единый математический объект. Матрицы будем обозначать прописными латинскими буквами -- A,B,Cи т.д. Более компактная запись матрицы (1) следующая:. Очень часто ссылку "" на размер матрицы A будем опускать, записывая ее короче:. Две матрицы равны, если, во-первых, совпадают их размеры, а во-вторых, на одинаковых местах стоят равные друг другу числа. Матрицы

;

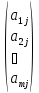
называются i- ой строкой иj- ым столбцом матрицы.

Матрица, у которой число строк и столбцов совпадают, называется квадратной. Элементы называются главной диагональю матрицы.

Матрица A называется верхнетреугольной, если ниже главной диагонали матрицы A стоят нули. Аналогично, A - нижнетреугольная матрица, если выше главной диагонали матрицы A стоят нули. Матрица A треугольная, если она либо верхнетреугольная, либо нижнетреугольная. Треугольная матрица с нулями на главной диагонали называется строго треугольной.

2. Сложение матриц, умножение на число и транспонирование

Матрицы можно складывать поэлементно, если они имеет одинаковый размер, а также поэлементно можно умножать матрицу слева и справа на число. Иными словами,

Транспонирование матрицы -- операция над -матрицей A , превращающая ее в–матрицу, у которой-ый коэффициент равен-ому коэффициенту матрицы A . Свойства операции транспонирования следующие:

Т1. ;

Т2. ;

Т3. ;

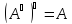3. Произведение матриц

Произведение строки на столбецтого размера определяется как число – матрица 1х1 равная. Произведениемматрицынаматрицуназываетсяматрицатакая, что

Теорема. Произведение матриц ассоциативно.

Единичная матрица есть квадратная матрица, у которой на главной диагонали единицы, а остальные все коэффициенты 0,

Предложение.Единичная матрица -- нейтральный элемент по отношению к произведению матриц, то естьдля любой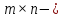матрицыA.

Докажем это предложение, записав - коэффициент единичной матрицы как. По определению

, еслии равно 0, если

Таким образом, определенная величина называется символом Кронекера.

Относительно транспонирования произведение матриц обладает следующим свойством

Т4. .

4. Определители

Определение.Пусть--n×n-матрица (. Определителем матрицы A называется число, которое вычисляется по следующему правилу

где -- определитель матицы, полученной извычеркиванием первого столбца и-- го столбца.

Теорема 1.Определитель треугольной матрицы равен произведению элементов на главной диагонали. В частности,.

Доказательство – индукция по 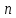с разложением по первому столбцу.□

Приступим к изучению свойств определителей. Доказывать мы их, как правило, не будем, все они проверяются непосредственно для 2х2 и 3х3-матриц.

Свойство 1.Определитель матрицы равен определителю транспонированной матрицы.

В силу равенства все свойства, доказанные для строк, автоматически переносятся на столбцы и наоборот. В частности

Функция переменных виданазывается линейной. Она обладает свойством

Наоборот, любая функция n переменных, обладающая свойством (2) линейна.

Свойство 2 (полилинейность).Определитель -- линейная функция от каждой строки (каждого столбца) матрицы.

Свойство 3 (кососимметричность). Определитель меняет знак при перемене местами двух строк (двух столбцов).

Свойство 4.Определитель равен нулю, если какие-либо две строки (два столбца) совпадают.

Действительно, при перестановке этих двух равных строк с одной стороны определитель не меняется (так как строки равны), а с другой стороны он меняет знак на по свойству кососимметричности. Имеем равенство из которого немедленно следует равенство.

Свойство 5.Определитель с нулевой строкой (столбцом) равен нулю.

Свойство 6.Определитель не изменится, если над строками (столбцами) совершить элементарное преобразование первого типа, т.е. к одной строке прибавить другую, умноженную на какое-либо число. То же верно и для столбцов.

Доказательство. Это утверждение -- следствие полилинейности и свойства Г:

Здесь F -- любая полилинейная и кососимметричная функция строк. □

Определение.-ым минором матрицы A называется определитель матрицы, получающейся из A вычеркиванием i -ой строки и j -го столбца. Обозначается этот минор --. Алгебраическим дополнением–го элемента матрицы A называется величина.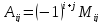

Свойство 7.Разложение определителя по j -му столбцу и i -ой строке:

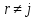Имеют место также ложные разложения по r -ой строке и r -ому столбцу; если и, то

Действительно, правая часть здесь совпадает с определителем матрицы, у которой две строки (два столбца) совпадают.