MATEMATIKA_EKZAMEN / ЛЕКЦИИ2 / Тема 3 Функции
.docxТема 3 Функции
Отображение множеств. Биекции. Композиция отображений. Обратное отображение. Последовательности. Матрицы, строки. Аналитические выражения. Функции одной и нескольких переменных, в т.ч. заданные аналитическим выражением. ОДЗ и область значений функции. График функции. Основные элементарные функции. Линейные функции. Квадратные трехчлены. Многочлены. Рациональные дроби. Элементарные функции.
Пусть
M и N – два множества. Правило
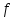 ,
в силу которого каждому элементу
,
в силу которого каждому элементу
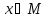 (аргумент) сопоставляется значение
(образ)
(аргумент) сопоставляется значение
(образ)
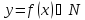 называется отображением из множества
N в множество M.
При этом множество M называется областью
допустимых значений (ОДЗ) отображения
называется отображением из множества
N в множество M.
При этом множество M называется областью
допустимых значений (ОДЗ) отображения
 ,
а множество
,
а множество

называется
областью значений отображения
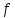 .
Очевидно, что
.
Очевидно, что
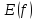 есть подмножество множества N. Если
есть подмножество множества N. Если
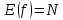 ,
т.е. если для всякого
,
т.е. если для всякого
 найдется хотя бы один аргумент
найдется хотя бы один аргумент
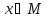 такой, что
такой, что
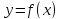 ,
то
,
то
 назовем отображением множества M
на множество N.
назовем отображением множества M
на множество N. 
Композиция
отображений
 и
и
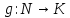 есть отображение
есть отображение
 такое, что
такое, что
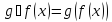
для
любого
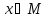 .
.
Среди
всех отображений M на себя
имеется выделенное – тождественное
отображение
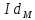 .
Оно оставляет всякий элемент
.
Оно оставляет всякий элемент
 на месте.
на месте.
Два
отображения
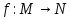 и
и
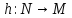 называют взаимно обратными, если
называют взаимно обратными, если
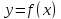 в том и только том случае, если
в том и только том случае, если
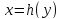 .
Это равносильно тому, что
.
Это равносильно тому, что
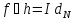 и
и
 одновременно. По другому, f
и h называют взаимно
обратными биекциями. Вообще, отображение
одновременно. По другому, f
и h называют взаимно
обратными биекциями. Вообще, отображение
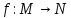 биективно, когда оно отображает M
на все N и, кроме того,
обладает взаимной однозначностью:
биективно, когда оно отображает M
на все N и, кроме того,
обладает взаимной однозначностью:
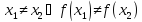
Пример.
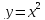 биективно отображает ℝ
на
биективно отображает ℝ
на
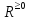 .
Обратным отображением будет
.
Обратным отображением будет
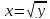 .
.
Функции
 и
и
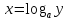 взаимно обратны.
взаимно обратны.
Если
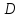 -- какое-либо числовое множество, а
-- какое-либо числовое множество, а
 -- правило, в силу которого каждому числу
-- правило, в силу которого каждому числу
 из
из
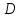 ставится в соответсвие число
ставится в соответсвие число
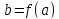 ,
то мы будем говорить, что задана функция
,
то мы будем говорить, что задана функция
 на множестве
на множестве
 .
Графиком функции
.
Графиком функции
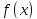 называется линия на декартовой плоскости,
состоящая из точек
называется линия на декартовой плоскости,
состоящая из точек
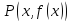 .
.
Пример.
Самой простой функцией является
тождественная
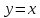 .
Ее график – биссектриса первого и
третьего квадрантов. Отправляясь от
такой функции с помощью арифметических
операций можно получить любой многочлен:
.
Ее график – биссектриса первого и
третьего квадрантов. Отправляясь от
такой функции с помощью арифметических
операций можно получить любой многочлен:
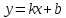 -- линейная функция, т.е. многочлен первой
степени ( здесь
-- линейная функция, т.е. многочлен первой
степени ( здесь
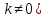
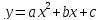 -- квадратный трехчлен, т.е. многочлен
второй степени (здесь
-- квадратный трехчлен, т.е. многочлен
второй степени (здесь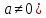
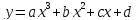 – кубический многочлен (здесь
– кубический многочлен (здесь
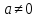 )
)
График функции
 или,
более общо,
или,
более общо,
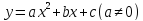 называется параболой. График функции
называется параболой. График функции
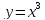 называется
кубической параболой. У параболы
называется
кубической параболой. У параболы
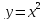 точка
точка
 есть точка глобального минимума, т.е.
в ней достигается наименьшее значение,
равное 0. Кубическая парабола
есть точка глобального минимума, т.е.
в ней достигается наименьшее значение,
равное 0. Кубическая парабола
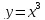 в точке 0 касается оси Ох, однако возрастает
в этой точке и вообще на всей числовой
оси; сама точка O(0,0) будет точкой
в точке 0 касается оси Ох, однако возрастает
в этой точке и вообще на всей числовой
оси; сама точка O(0,0) будет точкой
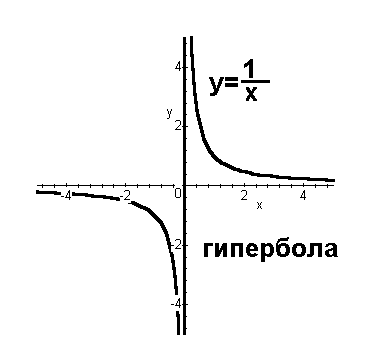
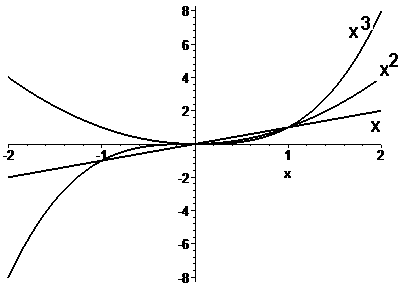
Рисунок 1. Гипербола
Рисунок 2. Id и параболы
перегиба.
Если допустить и операцию деления, то
из тождественной функции можно получить
функцию
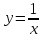 .
Здесь, не любое значение можно подставлять
вместо
.
Здесь, не любое значение можно подставлять
вместо
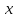 .
Естественной областью определения для
такой функции является числовая ось с
выброшенным нулем:
.
Естественной областью определения для
такой функции является числовая ось с
выброшенным нулем:

График
функции
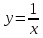 или, более общо, функции
или, более общо, функции
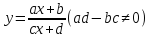 называется гиперболой.
называется гиперболой.
Гипербола
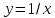 терпит разрыв в нуле, график этой функции
имеет две ветви. Каждая из ветвей на
бесконечности сколь угодно близко
подходит к оси Ох. Этот факт имеет
следующую запись:
терпит разрыв в нуле, график этой функции
имеет две ветви. Каждая из ветвей на
бесконечности сколь угодно близко
подходит к оси Ох. Этот факт имеет
следующую запись:
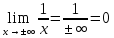 (см. параграф “Предел функции»).
(см. параграф “Предел функции»).
Можно
задавать функцию таблицей из двух строк,
где в первой строке перечислены все
возможные аргументы, а во второй –
соответствующие им значения. В математике
чаще прибегают к аналитическому способу
задания функции. Функция задается
аналитическим выражением, в которое
входят переменная
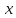 ,
константы и известные и точно определенные
операции (арифметические, корни,
логарифмы, показательные функции,
тригонометрические и т.п.) Естественной
ОДЗ аналитического выражения называется
совокупность всех чисел, при которых
все операции, входящие в аналитическое
выражение определены, и получается
итоговый результат --
,
константы и известные и точно определенные
операции (арифметические, корни,
логарифмы, показательные функции,
тригонометрические и т.п.) Естественной
ОДЗ аналитического выражения называется
совокупность всех чисел, при которых
все операции, входящие в аналитическое
выражение определены, и получается
итоговый результат --
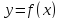 .
.
Пример.
Естественная ОДЗ функции
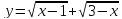 есть отрезок
есть отрезок
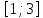 .
.
Список основных элементарных функций
-
Степенные
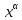
-
Показательные

-
Логарифмические
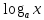
-
Тригонометрические

-
Обратные тригонометрические