3. Методы решения некоторых дифференциальных уравнений первого порядка

Определение.Общим решением дифференциального уравнения

в области называется такая функцияy=𝜑(x,C), что

1) для любого значения константы C,-- решение дифференциального уравнения (*);

2) для любых начальных условий найдется константатакая, что.

Например, -- общее решение дифференциального уравненияy'=yна всей декартовой плоскости, а-- частное решение, или решение задачи Коши с начальным условием.

1. Уравнения с разделяющимися переменными

Дифференциальное уравнение вида

называется уравнением с разделяющимися переменными. Метод решения этого уравнения следующий:

а) записываем производную в дифференциалах:;

б) разделяем переменные и получаем уравнение в дифференциалах : ;

в) интегрируем уравнение в дифференциалах: (константуCзаписываем лишь одну) -- получаем общее решение в неявном виде;

г) выражаем yчерезxиC-- получаем общее решение в явном виде.

Заметим, что такой же метод решения применим и дифференциальному уравнению в дифференциалах, имеющему вид

Пример. Решим уравнение

Следует рассмотреть два случая 1) ; 2). Ответ

Пример. Решим дифференциальное уравнение, описывающее протекание химической взрывной реакции --. Здесьx(t) -- количество продуктов взрыва в момент времениt, аk>0 -- коэффициент пропорциональности. Методом, изложенным выше, разделяем переменные, интегрируем --и находим общее решениеЕсли, тои количество вещества становиться бесконечным за конечное время.

2. Однородные уравнения

Так называются уравнения вида

Метод решения:

а) переходим к новой неизвестной функции . Тогдаи уравнение (2) переписывается так:(*). А это уравнение с разделяющимися переменными.

б) Решаем вспомогательное уравнение (*). Пусть есть его общее решение.

в) Тогда -- общее решение исходного уравнения.

Пример (форма прожектора).Найдем форму прожектора – поверхности вращения графика функциивокруг оси Оу такой, что луч света, исходящий из фокуса, помещенного в начале координат и отраженного от данной поверхности выходит пучком линий параллельных оси Оу.

Пользуясь физическим законом «угол падения равен углу отражения», составим соответствующее дифференциальное уравнение. Рассмотрим точку на графике функции. Тогда векторb, направленный по касательной в этой точке имеет координаты. Имеем

Путем алгебраических преобразований, последнее уравнение сводится к дифференциальному уравнению

Заменяя , получим, откуда. Интегрируя, получаем. Переносяuв право, и возводя в квадрат, имеем:

-- семейство парабол с фокусом в начале координат.

3. Линейные дифференциальные уравнения первого порядка

Так называются уравнения вида

Если P(x),Q(x) непрерывны, то условия теоремы существования и единственности выполнены.

Метод решения

а) Решаем сначала уравнение без правой части как уравнение с разделяющимися переменными. Получаем общее решение в видеy(x)=Cu(x), где-- одна из первообразных функции.

б) Общее решение уравнения (4) ищем в виде y=C(x)u(x), гдеC(x) -- функция, подлежащая определению. Такой приём называется методом вариации постоянных.

в) Подставляя в (4), имеем:

Второе и третье слагаемые в левой части дают 0, ибо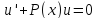. Отсюда

г) Решая это уравнение, т.е. интегрируя, находим

д) Подставляя это в , получаем общее решение исходного уравнения.

Пример.Сила токав электрической цепи с омическим сопротивлениемRи коэффициентом самоиндукцииLудовлетворяет дифф. уравнению

где E-- электродвижущая сила. Найдём зависимостьj(t) при условии, что. Полагая сначалаE=0 находим, где. Тогда решение исходного уравнения ищем в виде. ФункциюC(t) находим из уравнения. Интеграл функцииравен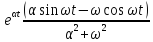. Отсюда

В частности, в установившемся режиме (время tвелико) амплитуда колебаний будет равна

При надо вместо уравнения (5) решать уравнение( закон Ома). Получаем.