Дифференциальные уравнения первого порядка

Оглавление

1Основные понятия 1

2Задачи, приводящие к дифференциальным уравнениям 3

2.1Уравнение размножения и гибели. 3

2.2Уравнение движения точки на оси 6

3Методы решения некоторых дифференциальных уравнений первого порядка 7

3.1Уравнения с разделяющимися переменными 8

3.2Однородные уравнения 9

3.3 Линейные дифференциальные уравнения первого порядка 10

3.4Уравнение в полных дифференциалах 11

1. Основные понятия

Ранее неоднократно мы встречались с уравнениями с одним неизвестным; при этом корнем или решением такого уравнения служило число, при подстановке которого вместо неизвестного, уравнение превращалось в верное числовое равенство. В этом разделе мы будем решать уравнения, неизвестным в которых является функция. В разделе «Неопределенный интеграл» мы фактически занимались решением дифференциального уравнения

Требовалось найти такую функцию (первообразную) , производная которой тождественно равна. Мы видели, что решений у уравнения (1) бесконечно много, и все они отличаются друг от друга на константу (теорема о первообразных). Эту множественность решений можно обозревать и с другой точки зрения. Фиксируем значение первообразной в определенной точке:

Считаем начальными условиями. Тогда для непрерывной функции, заданной на интервалеи начальных условийcусловиемсуществует и единственно решениеуравнения (1), удовлетворяющее соотношению (2). Более того, ответ задается формулой

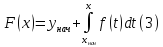
Сформулирована теорема существования и единственности для дифференциального уравнения самого простого вида. Рассмотрим теперь уравнение вида

Его полное название – обыкновенное дифференциальное уравнение первого порядка в нормальной форме. Обыкновенное, так как неизвестная функция зависит лишь от одной переменной, в отличии, например, от уравнения ЛапласаПервого порядка – так как старшая производная, входящая в уравнение (4) имеет первый порядок. Нормальная форма записи дифференциального уравнения означает, что старшая производная выражена через младшие производные, а также саму неизвестную функцию, а также переменную. Таким образом,

есть дифференциальное уравнение второго порядка в нормальной форме, а

есть общий вид дифференциального уравнения n-го порядка в нормальной форме. Решение уравнений вида (4) составляет основную задачу данной темы. При этом функция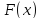называется (частным) решением уравнения (4) или (6), если при подстановки вместов это уравнение получаем тождество.

Пример. Функция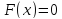также как и функциябудут решениями дифференциального уравненияcодним и тем же начальным условием

Задача решения дифференциального уравнения с заданными начальными условиями (например, найти решение уравнения (4)cусловием (2)) называется задачей Коши. Начальные условия для уравнения (6) задаются рядом чисели выглядят так

Теорема существования и единственности.Если в дифференциальном уравнении первого порядка (4) функциявместе со своей частной производной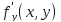непрерывны в области, содержащейкак свою внутреннюю точку, то найдется интервал, для которого существует и единственно решениезадачи Коши.

Общая теорема для уравнения n-го порядка (6) гласит, что если функциявместе со всеми своими частными производными по второй, третьей и т.д. поn-ой переменной непрерывны в пространственной области, содержащей точку, то локальное решение задачи Коши существует и единственно.

В примере выше нарушена единственность решения задачи Коши, так как производная не будет непрерывной в начале координат.