Длина интервала на числовой прямой
Пусть
точки
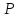 и
и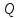 имеют координаты
имеют координаты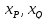 на числовой оси. Тогда длина интервала
(отрезка) с концами
на числовой оси. Тогда длина интервала
(отрезка) с концами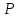 и
и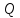 вычисляется по формуле
вычисляется по формуле
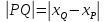
Пример. Расстояние от точки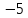 до точки
до точки равно
равно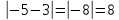 .
.
Расширенная область действительных чисел
Присоединим
к
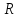 два элемента --
два элемента -- и
и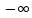 ,
полагая, что для всех
,
полагая, что для всех
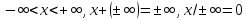
Для
всех положительных
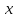 будем считать, что
будем считать, что
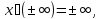
а
для отрицательных
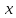 --
--
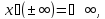
Полагаем
также
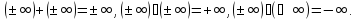
Таким
образом, неопределенными остаются
операции:
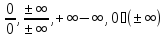
Вещественные
числа вместе с
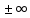 образуютрасширенную числовую прямую.
Можно убедиться, что основные
арифметические правила (ассоциативность,
коммутативность, дистрибутивность)
остаются верными и для расширенной
системы чисел, при условии определенности
всех входящих операций.
образуютрасширенную числовую прямую.
Можно убедиться, что основные
арифметические правила (ассоциативность,
коммутативность, дистрибутивность)
остаются верными и для расширенной
системы чисел, при условии определенности
всех входящих операций.
19


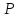 и
и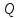 имеют координаты
имеют координаты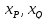 на числовой оси. Тогда длина интервала
(отрезка) с концами
на числовой оси. Тогда длина интервала
(отрезка) с концами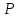 и
и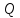 вычисляется по формуле
вычисляется по формуле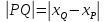
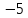 до точки
до точки равно
равно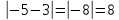 .
.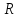 два элемента --
два элемента -- и
и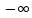 ,
полагая, что для всех
,
полагая, что для всех
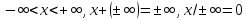
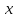 будем считать, что
будем считать, что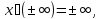
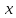 --
--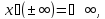
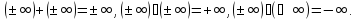
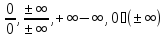
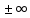 образуютрасширенную числовую прямую.
Можно убедиться, что основные
арифметические правила (ассоциативность,
коммутативность, дистрибутивность)
остаются верными и для расширенной
системы чисел, при условии определенности
всех входящих операций.
образуютрасширенную числовую прямую.
Можно убедиться, что основные
арифметические правила (ассоциативность,
коммутативность, дистрибутивность)
остаются верными и для расширенной
системы чисел, при условии определенности
всех входящих операций.