
- •Оглавление
- •Натуральные числа
- •Целые числа
- •Рациональные числа
- •Поле действительных чисел
- •Несоизмеримость диагонали квадрата и его стороны
- •Бесконечные десятичные дроби
- •Координаты на числовой оси
- •Сложение и умножение действительных чисел
- •Аксиоматическое определение поля действительных чисел
- •Следствия из аксиом порядка
- •Следствия из аксиомы о верхней грани
- •Степени и корни
- •Длина интервала на числовой прямой
- •Расширенная область действительных чисел
Следствия из аксиом порядка
Имеют место соотношения
A.Если (
(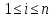 ),
то
),
то
Б.Если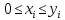 (
( ),
то
),
то
Наибольшее
из чисел
 будем обозначать
будем обозначать ,
а наименьшее --
,
а наименьшее -- .
.
Для строгих неравенств выполняются такие правила
В.Если то
то
Г.Если ,
а
,
а ,
то
,
то .
Если же
.
Если же ,
то
,
то .
.
Д.
Если или
или ,
то
,
то .
.
Е.(транзитивность отношения <) Если и
и ,
то
,
то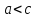
Следствия из аксиомы о верхней грани
Принцип
Архимеда.А.Для любого вещественного
числа r и сколь угодно малого𝜺>0 найдется натуральное число N такое,
что .
.
Б.Пусть .
Для любого вещественного числа b найдется
натуральное
.
Для любого вещественного числа b найдется
натуральное такое, что
такое, что .
.
Обоснуем
этот принцип. Если N𝜺<r для всех натуральных N, то определено
число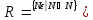 .
Так как R -- точная верхняя грань, то
.
Так как R -- точная верхняя грань, то для какого-либо
для какого-либо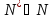 .
Но тогда
.
Но тогда в противоречии с тем, что R -- верхняя
грань. Противоречие показывает, что
множество
в противоречии с тем, что R -- верхняя
грань. Противоречие показывает, что
множество неограничено сверху, а значит
неограничено сверху, а значит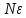 превзойдет любое наперед заданное
число.
превзойдет любое наперед заданное
число.
Второе утверждение доказывается по такой же схеме.□
Следствие.
Для любого𝜺>0 найдется натуральное число N для
которого 1/N<𝜺. Аналогично, если 0≤ d<1 и𝜺>0, то найдется N для которого .
.
Заметим, что «на вид» рациональная прямая, т.е. совокупность всех рациональных точек, выглядит как сплошная линия. Объясняется это плотностью множества рациональных точек на прямой.
Теорема
(плотность
 в
в
 ).Каждый непустой интервал
).Каждый непустой интервал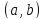 содержит рациональную точку.
содержит рациональную точку.
Доказательство.
Считаем
 .
Найдем
.
Найдем такое, что 1/n<b-a (следствие принципа
Архимеда).Cнова применяя
принцип Архимеда, получаем целое число
m такое, что m/n>a. Пусть m наименьшее с
таким свойством. Если бы m/n≥ b, то
такое, что 1/n<b-a (следствие принципа
Архимеда).Cнова применяя
принцип Архимеда, получаем целое число
m такое, что m/n>a. Пусть m наименьшее с
таким свойством. Если бы m/n≥ b, то -- противоречие с минимальностью m.
Противоречие показывает, что на самом
делеm/n<b,
тем самым
-- противоречие с минимальностью m.
Противоречие показывает, что на самом
делеm/n<b,
тем самым .□
.□
Следствие.Каждый непустой интервал содержит бесконечно много рациональных точек.
Принцип вложенных отрезков Кантора. Для всякой системы вложенных друг в друга отрезков существует общая точка.
Доказательство.
Пусть
 --
система вложенных отрезков. Тогда
множество
--
система вложенных отрезков. Тогда
множество ограничено
сверху любым
ограничено
сверху любым .
Отсюда вытекает, что
.
Отсюда вытекает, что -- общая точка отрезков
-- общая точка отрезков .
.
Степени и корни
Для
любого числа
 и любого положительного целого числа
и любого положительного целого числа определимстепень
определимстепень

Распространим степени на нулевой и отрицательные показатели:

(предполагаем
здесь
 .
Имеют место формулы:
.
Имеют место формулы:

Для
любого
 найдется единственное неотрицательное
действительное число, квадрат которого
равен
найдется единственное неотрицательное
действительное число, квадрат которого
равен .
Его обозначают
.
Его обозначают и называютквадратным корнем из
и называютквадратным корнем из
 .
Квадратный корень равен
.
Квадратный корень равен или
или .
.
Например,
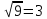 .
Заметим, что
.
Заметим, что не смотря на то, что
не смотря на то, что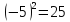 .
Квадратные корни из отрицательных чисел
будут числами новой природы (комплексные
числа). Более общо, имеет место
.
Квадратные корни из отрицательных чисел
будут числами новой природы (комплексные
числа). Более общо, имеет место
Теорема.Для любого найдется единственное неотрицательное
действительное число, n-ая степень
которого равен
найдется единственное неотрицательное
действительное число, n-ая степень
которого равен .
А именно
.
А именно

Его
обозначают
 и называюткорнем n-ой
степени из
и называюткорнем n-ой
степени из
 .
.
Доказательство
для n=2. Множество ограничено сверху и не пусто. Следовательно,
существует точная верхняя грань
ограничено сверху и не пусто. Следовательно,
существует точная верхняя грань .
Если бы
.
Если бы ,
то
,
то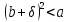 для достаточно малого положительного
для достаточно малого положительного (можно взять
(можно взять ,
тогда
,
тогда ).
Это, однако, противоречило бы тому, что
).
Это, однако, противоречило бы тому, что – точная верхняя грань. Аналогично,
неравенства
– точная верхняя грань. Аналогично,
неравенства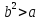 не может быть. Остается только один
возможный случай – равенство
не может быть. Остается только один
возможный случай – равенство .
.
Выполняются следующие правила обращения с корнями:

После
этого можно определить для любого
рационального числа
 с
с и любого
и любого степень с рациональным показателем:
степень с рациональным показателем:

Для такой степени выполняются по-прежнему правила (4).
Если
целое число
 нечетное, то можно определить квадратный
корень n-ой степени из отрицательного
числа
нечетное, то можно определить квадратный
корень n-ой степени из отрицательного
числа как такое единиственное (отрицательное)
число,n-ая степень которого
равна
как такое единиственное (отрицательное)
число,n-ая степень которого
равна .
Например,
.
Например, ,
,
Модуль
Число

называется
абсолютной величиной или модулем
числа
 .
.
Свойства модуля
М1. или более общо
или более общо
М2.
(неравенство треугольника) или более общо
или более общо

М3.
(непрерывность модуля)
M4.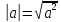
Знак числаопределяется как функция равная 1, если
равная 1, если и равная
и равная ,
если
,
если .
Имеем равенство
.
Имеем равенство

для любых двух ненулевых чисел.
