5. Аксиоматическое определение поля действительных чисел

Поле действительных чисел можно описать аксиоматически как совокупность чисел 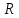, на которой заданы две операции – сложение и умножение, а также отношение порядка” и которые подчиняются следующим правилам:

RA1. (ассоциативность сложения) Для любых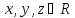выполняется равенство.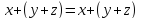

RA2.(коммутативность сложения) Верно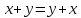для любых.

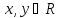RA3. (нейтральный элемент сложения) Существует элемент«ноль» такой, что для любогоимеет место равенство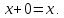

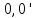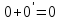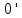Нулевой элемент единственен. Действительно, пусть -- два нулевых элемента. Тогда, так как-- нулевой элемент, итак как– нулевой элемент. Отсюда вытекает равенство.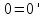

RA4. (противоположный элемент) Для любогонайдется элементтакой, что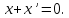

Противоположный элемент единственен -- см. далее доказательство единственности обратного элемента. Противоположный элемент к элементу 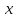обозначается.

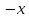Множество, на котором задана операция “+” (вместо знака «плюс» может быть знак умножения, звездочка, кружочек и т.п.) называется абелевой группой.

Нильс Хе́нрик А́бель (норв. Niels Henrik Abel; 5 августа 1802 — 6 апреля 1829,) —норвежский математик.Родился в семье пастора. Детство Абеля было омрачено слабым здоровьем, а также пьянством и постоянными раздорами его родителей. Доказал, что любые уравнения степени выше 4-й, вообще говоря, неразрешимы в радикалах. Причём он привёл конкретные примеры неразрешимых уравнений. Умер в 27 лет от туберкулеза.В его честь был назван кратер Абель на Луне.

RM1. (ассоциативность умножения) Выполняется тождественно.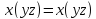

RM2. (нейтральный элемент умножения) Существует элемент единица, который обозначается 1 и такой, что для любого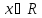имеет место равенство.

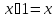Единичный элемент единственен -- см. единственность нуля.

RM3. (дистрибутивность) Для любыхимеет место равенство.

Множество с двумя операциями сложения и умножения, относительно которых выполнены аксиомы RA1-RA4 (т.е. относительно сложения это множество – абелева группа), а также аксиомыRM1-RM3 называетсякольцом.

RM4. (коммутативность умножения) Верно тождество.

Кольцо с дополнительной аксиомой RM4 коммутативности умножения называетсякоммутативным кольцом.

RM5. (обратный элемент) Для любого ненулевого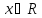найдется элемент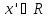такой, что

Обратный элемент единственен. Докажем это. Пусть -- два обратных элемента к. Тогда

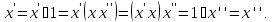
Заметим, что при доказательстве единственности обратного элемента коммутативность умножения не используется. Обратный элемент к элементу 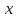обозначается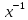или.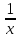

Коммутативное кольцо, в котором каждый ненулевой элемент обратим, т.е. выполнена аксиома RM5, называетсяполем.

RL1. (линейность порядка) Для любыхлиболибо.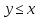

RL2. (рефлексивность)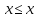для любого x.

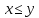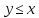RL3. (антисимметричность) Изиследует равенство.

RL4. (транзитивность) Для любых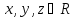изиследует.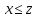

Произвольное множество с отношением ≤ , относительно которого выполняются аксиомы RL2-RL4, называетсячастично упорядоченным множеством. Если же в нем выполнена и аксиомаRL1, то оно называетсялинейно упорядоченным множеством (л.у. множеством), а само отношение “≤” называетсяотношением линейного порядка.

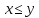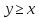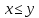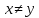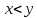Отношение записывается также как. Еслии, то говорим, чтострого меньше, чеми записываем это какили.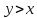

Если 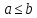– элементы л.у. множества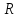, то

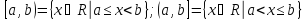
называют соответственно интервалом, отрезком и полуинтервалом.

RL5. Из неравенства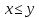следует неравенстводля любого z.

RL6. Изследует.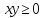

Поле, на котором определено отношение линейного порядка, и выполняются аксиомы RL5,RL6 называетсялинейно упорядоченным полем.

Подмножество A поля действительных чисел (или, более общо, любого линейно упорядоченного множества) называется ограниченным сверху (снизу), если найдется число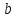, называемое верхней (нижней) границей или гранью такое, что для любого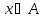следует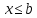(∀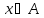следует). Ограниченное сверху и снизу множество называютограниченным. Верхняя грань множества A называетсяточной верхней граньюи обозначается sup A (читается: «супремум»), если она меньше любой другой верхней грани. Аналогично определяетсяточная нижняя грань-- inf A (читается: «инфинум») как наибольшая из всех нижних граней.

Последней аксиомой в описании поля действительных чисел будет

Аксиома верхней грани. Любое непустое ограниченное сверху подмножество множества действительных чисел имеет точную верхнюю грань.

Аксиоматика вещественных чисел закончена.

Аксиома точной верхней грани в поле рациональных чисел не выполняется, как показывает пример множества рациональных чисел меньших 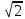, не имеющего точной верхней грани в областиℚ.

Оказывается поле действительных чисел единственно, в том смысле, что если – какое-либо множество с операциями сложения и умножения, а также с отношением порядка подчиняющееся всем перечисленным выше аксиомам, то существует биекция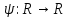такая, что

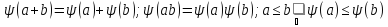
для любых двух элементов .
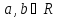