1. Несоизмеримость диагонали квадрата и его стороны

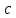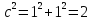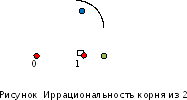
Напомним, что по теореме Пифагора квадрат гипотенузы в прямоугольном треугольнике равен сумме квадратов катетов. Следовательно, в равнобедренном прямоугольном треугольнике с катетами равными единице гипотенуза удовлетворяет соотношению. Отложим в положительном направлении на числовой оси эту гипотенузу (см. рис. 4). Получаем точку, которой должно соответствовать число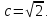Какова природа этого числа? Оказывается, что это число не является рациональным.

Теорема. Не существует рационального числа, квадрат которого равен двум.

Доказательство см. в параграфе «Методы доказательств».

Существуют много других иррациональных чисел -- 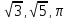и т. д. Итак, опять мы должны решать проблему расширения числовой системы до новой, включающей в себя, по крайней мере, все корни из положительных рациональных чисел и такое важное число «пи»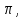-- отношение длины окружности к диаметру (оно не выражается ни через какие корни из рациональных чисел).

2. Бесконечные десятичные дроби

Бесконечной десятичной дробьюназывают бесконечную сумму (т.е. ряд) вида

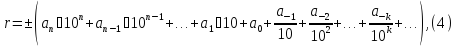
где все 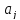– цифры, а впереди стоит либо знак «+», либо знак «-». При этом конечную десятичную дробь

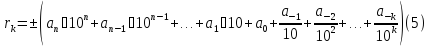
назовем приближением дроби (4) с точностью 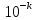. Знак «+» обычно опускают. Более кратко, бесконечную десятичную дробь (4) записывают как

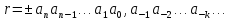
Например, .

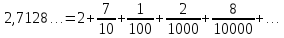Заметим, что рациональные числа изображаются периодическими бесконечными десятичными дробями. Например,

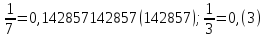
Для представления рационального числа в виде (периодической) бесконечной десятичной дроби мы просто делим уголком числитель на знаменатель. Для того, что бы представить периодическую десятичную дробь в виде рационального числа нужно воспользоваться теоремой о сумме геометрической прогрессии:

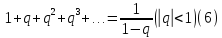
Формально, соотношение (6) можно проверить, умножая ряд 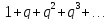на знаменатель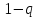, раскрывая скобки и убеждаясь, что все сокращается кроме 1. Вопросы сходимости этого ряда и законности процедуры умножения разобраны в главе «Ряды». Например,

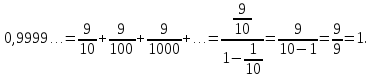
Итак, 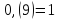. По этой причине бесконечную дробь вида

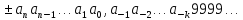
отождествляют с дробью 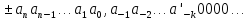, где предполагается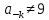и.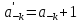

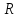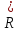Определение.Действительным числом назовем бесконечную десятичную дробь с учетом описанного выше отождествления. Совокупность действительных чисел обозначим. Числа из множестваназывают иррациональными.

Например, 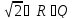, т.е.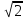-- иррационально, как было доказано выше.

Лексикографический порядок распространяется и на бесконечные десятичные дроби. Таким образом, ℝстановиться линейно упорядоченным множеством.

3. Координаты на числовой оси

Мы будем считать, что каждой точке 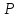на числовой прямой соответствует координата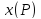-- действительное число. При этом, если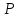лежит в положительном направлении от начала координат, то координата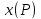это не что иное, как длина отрезка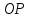. Если же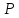лежит в отрицательном направлении от начала координат, то.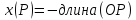

Пусть даны два действительных числа 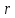и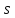, как координаты точек P и Q. Тогда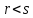тогда и только тогда, когда точка P лежит левее точкиQ.

4. Сложение и умножение действительных чисел

Покажем на примере 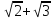, как складываются две бесконечные десятичные дроби. Воспользовавшись калькулятором, получаем:

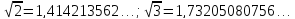
Складывая приближения с одним, двумя, тремя и т.д. десятичными знаками после запятой, вычисляем:

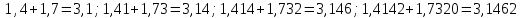
Получаем приближения бесконечной десятичной дроби 3,146264369941972342…, которая и есть сумма 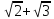. Перемножаются бесконечные десятичные дроби по тому же принципу – перемножают их все более точные приближения, а затем следят, к какой бесконечной десятичной дроби стремятся эти приближения:

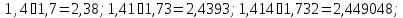
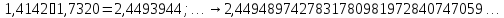
Здесь не так быстро как для сложения получаются «верные» десятичные знаки. Три верных знака мы получили, лишь вычислив произведение приближений с точностью до

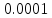
Умножение распространяется на все действительные числа при помощи правила знаков:

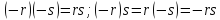
Определение сложения и умножения двух бесконечных десятичных дробе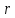й и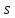таково:

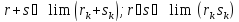
Предел здесь понимается в следующем смысле: для любого номера nнайдется такоеK(зависящее отn), что при любом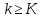n-ый десятичный знак рационального числа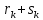один и тот же.

Теорема.Совокупностьℝвсех бесконечных десятичных дробей относительно определенных выше операций сложения и умножения образует поле действительных чисел в смысле следующего параграфа