3. Рациональные числа

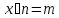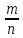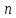Очень часто требуется разделить некоторую величину на n равных частей, т.е. решить уравнение . В кольце целых чисел такое уравнение не всегда разрешимо, и мы вновь встаем перед проблемой расширения системы чисел до более обширной, в которой сохраняются прежние алгебраические правила, и данное уравнение всегда разрешимо при.Рациональное числоесть дробь вида, где знаменатель-- целое число, отличное от 0, а числитель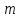-- произвольное целое число. Считаем

Отсюда следует правило сокращения: . Операции сложения и умножения над дробями определяются так

Совокупность всех дробей обозначим 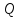и назовемполем рациональных чисел(термин «поле» объясняется далее в параграфе «Аксиоматика поля действительных чисел»). Поле рациональных чисел действительно расширяет кольцо целых чисел. Мы можем отождествлять дробь видас целым числом, ибо операции сложения и умножения (2) при подстановкепревращаются в сложение и умножение над целыми числам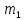ии.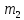

Как геометрически интерпретировать рациональные числа? Прежде всего, дробь 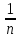при натуральном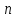изображается концом отрезка на числовой оси, который получается делением единичного отрезка OEна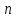равных частей. Заметим, что это можно сделать с помощью циркуля и линейки (без делений). Тогда для любого другого натурального числа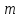дробьизображается точкой, которая получаетсяmкратным откладыванием отрезка, построенном на предыдущем шаге. Откладываем в положительном направлении. Если же нужно изобразить дробьпри отрицательном целом, то отрезок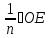откладываем от начала координат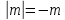раз в отрицательном направлении.

Поле рациональных чисел упорядочено – считаем, что дробь больше дроби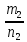, если точка, изображающая первую дробь, стоит правее, чем точка, изображающая первую дробь. Аналитически это проверяется так:

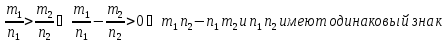
Например, 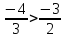так как.

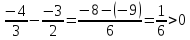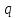Арифметические операции и отношение порядка согласованы в том смысле, что если , тодля любой дробиидля любой неотрицательной дроби.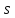

Рациональное число будет ненулевым тогда и только тогда, когда. В этом случае дробьявляется обратным рациональным числом, т.е..

Среди всех дробей особенно употребительны десятичные – это дроби вида (случай, когда знаменатель есть степень десяти). Любая десятичная дробь однозначно записывается в виде

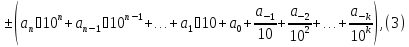
где все 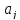– цифры, т.е целые числа от 0 до 9. Короче дробь вида (3) записывают как

Отметим, что сумма и разность, а также произведение двух десятичных дробей есть снова десятичная дробь. Иными словами, десятичные дроби образуют кольцо. Следует уметь складывать и перемножать десятичные дроби «столбиком». Следует также усвоить лексикографический принцип сравнения двух десятичных дробей. Пусть

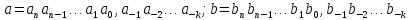
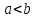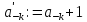-- две положительные десятичные дроби (одинакового количества разрядов можно всегда достичь, добавляя там, где надо нули). Тогда если и только, еслидля первого слева несовпадающего разряда. В частности, еслии, то

какие бы дополнительные разрядные цифры 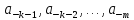мы ни добавляли. Для двух отрицательных десятичных дробей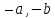 неравенствовыполняется в том и только том случае, когда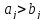для первого слева несовпадающего разряда.

4. Поле действительных чисел

В этом параграфе строиться поле действительных чисел 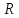, в котором возможны более сложные операции с числами, такие как, например, извлечение корней.