Числа

Оглавление

1Натуральные числа 1

2Целые числа 3

3Рациональные числа 3

4Поле действительных чисел 6

4.1Несоизмеримость диагонали квадрата и его стороны 6

4.2Бесконечные десятичные дроби 7

4.3Координаты на числовой оси 9

4.4Сложение и умножение действительных чисел 9

4.5Аксиоматическое определение поля действительных чисел 10

4.6Следствия из аксиом порядка 14

4.7Следствия из аксиомы о верхней грани 15

5Степени и корни 16

6Модуль 17

6.1Длина интервала на числовой прямой 18

7Расширенная область действительных чисел 18

Числа бывают различной природы: натуральные -- ℕ, целые --ℤ, рациональные --ℚ, вещественные --ℝ, комплексные --ℂ. Каждая следующая система чисел есть расширение предыдущей:

ℕ ⊂ ℤ ⊂ ℚ ⊂ ℝ ⊂ ℂ.

1. Натуральные числа

Натуральные числа, т.е. числа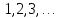получаются из единицы многократным применением операции сложения: 2=1+1; 3=2+1; …; 9=8+1;… Итак, множество натуральных чисел есть

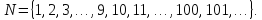
Множество натуральных чисел бесконечно. Первые девять натуральных чисел 1,2,…,9 и ноль 0 называются цифрами. При помощи цифр можно записать любое натуральное число, используя позиционную десятичную систему счисления:

Здесь 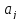-- цифры. Пользуясь такой системой счисления, удобно столбиком складывать и умножать числа.

Геометрическая интерпретация натуральных чисел --точки на прямой , которые получаются в результате откладывания с помощью циркуля выбранного заранее единичного отрезка в выбранном направлении. Такой интерпретацией мы далее будем пользоваться постоянно, поэтому сформулируем

Определение.Числовой осью называется прямая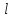, с выбранной на ней точкой O (начало отсчетаилиначало координат), выбранном одном из двухположительном направлениии выбранном отрезке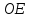, длину которого полагаем равным единице. Противоположное направление к выбранному положительному направлению называетсяотрицательным направлением.

Итак, мы начали приписывать точке на оси координату– число. Сейчас мы это сделали только для некоторых точек – концов отрезков. На множестве натуральных чисел вводится порядок: 1<2<3<… . Иными словами,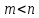для чисел, если и только если точкаP, соответствующая числуm(т.е.) лежит левее на числовой оси рис.1 чем точка Q, соответствующая числу n. Отношениенестрогого неравенства тогда получается из отношения строгого неравенства простой логической операцией: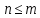по определению означает, что либо n=m, либо n<m. Например, 5 ≤ 5 -- верное высказывание.

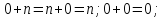
Присоединим к множеству натуральных чисел элемент ноль 0, обладающий свойствами для любого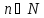. Получаем множество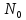всех целых неотрицательных чисел. Именно началу координат, точке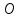, припишем нулевую координату.

2. Целые числа

На множестве натуральных чисел уравнение вида не разрешимо, вообще говоря, относительно. Чтобы исправить это, вводятся отрицательные целые числа. Это множество {-1,-2,-3,… }. Считаем, что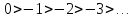и, таким образом, по определению неравенство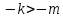для двух натуральных чисел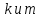имеет место тогда и только тогда, когда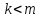. Совокупность как положительных так и отрицательных целых чисел, а также нуля называетсякольцом целых чисел ℤ(термин «кольцо» объясняется далее в п. «Аксиоматика поля действительных чисел»). Итак:

Целые отрицательные числа интерпретируются на числовой оси точками, которые получаются откладыванием единицы масштаба в отрицательном направлении (см. рис. 2)