Шамышева2 / ОСНОВЫ ТЕОРИИ СТОХАСТИЧЕСКИХ СИСТЕМ (Конспект лекций)

Контрольные вопросы.

1. Экспоненциальный закон распределения. Функция и плотность рас-

пределения. Параметры закона распределения.

2. Нормальный закон распределения. Функция и плотность распреде-

ления. Параметры закона распределения.

3.Стандартное нормальное распределение. Параметры распределения.

4.Влияние параметров нормального закона распределения на вид кри-

вой плотности распределения.

5.Вычисление вероятности попадания нормального распределения случайной величины в заданный интервал.

6.Правило «трех сигм», его содержание.

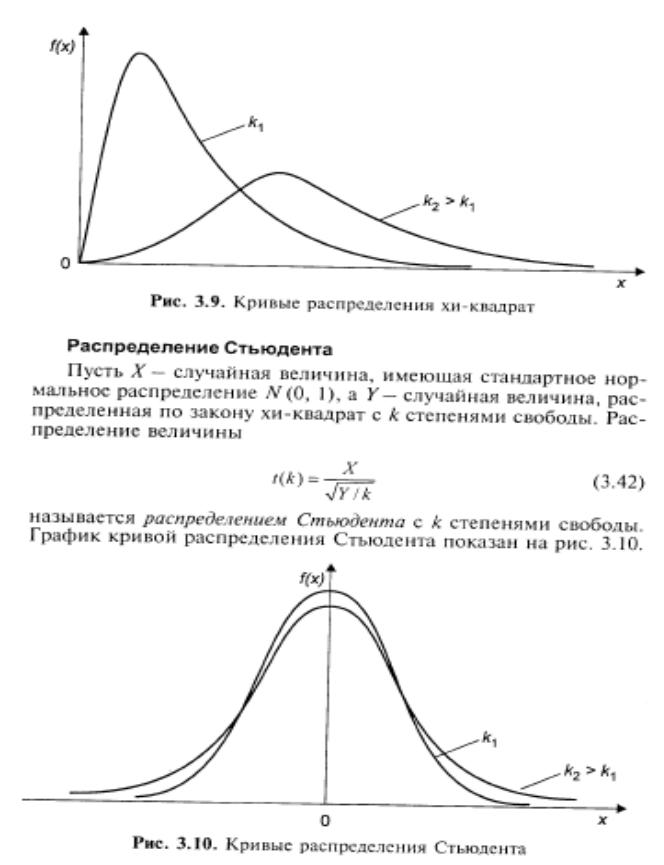
7.Распределение хи-квадрат. Параметры закона распределения.

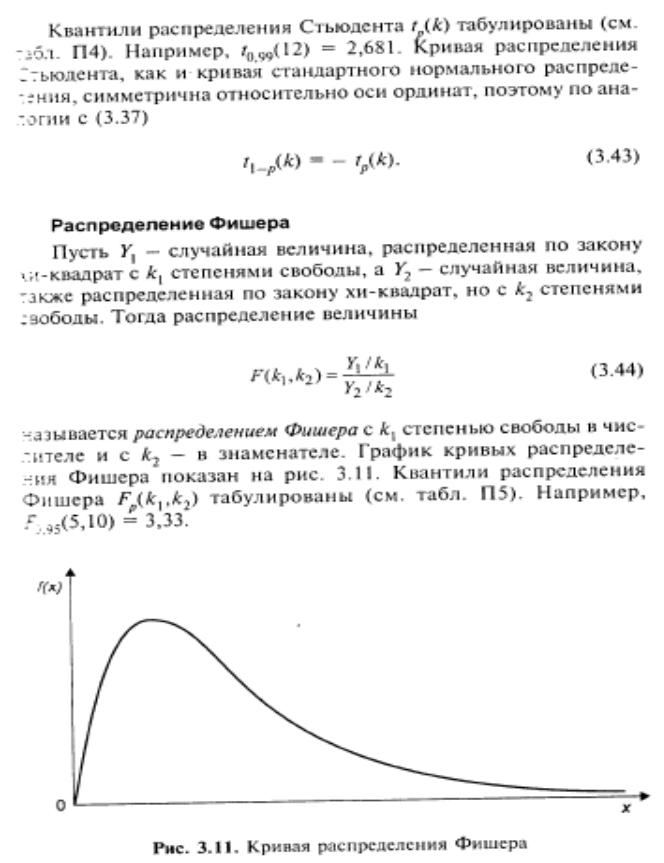
8.Распределение Стьюдента. Параметры закона распределения.

9.Распределение Фишера. Параметры закона распределения.

56

5.2. Двумерное нормальное распределение

Плотность распределения задается выражением [4]:

рXY(x,y)={1/(2πσXσY√(1-ρXY2)}e-1/2*Q(x,y), (1)

где Q(x,y) =1/(1-ρXY2){(x-mX)2/σX2+ (y-mY)2/σY2-2 ρXY(x-mX)/

σX(y-mY)/ σY}

здесь mx и my – центры распределения случайных величин X и Y,

σх и σу- стандартные отклонения случайных величин X и Y.

Выражение (1) является плотностью двумерного распределения двух линейно коррелированных величин X и Y, каждая из которых в отдельности нормально распределена с соответствующими значениями центра и диспер-

сии.

Если величины X и Y независимы и нормально распределены с плотно-

стями соответственно N(x, mx, σx) и N(y, my, σy), то плотность их совместно-

го распределения получается из (1) при ρXY=0 как произведение плотностей

N(x, mx, σx) и N(y, my, σy) их одномерных распределений:

ΨXY(x,y)={1/(2πσXσY}exp{-1/2*[(x-mX)2/σX2+ (y-mY)2/σY2 ]}

(2)

Из этого следует, если нормально распределенные величины не еаллированны, то они вместе с тем и независимы. Этот вывод не подходит

для произвольного закона распределения, а только для нормального.

Рассмотрим условное нормальное распределение, его плотность равна:

р(y/x)={1/(2πσY√(1-ρXY2)}exp{-1/2[((y-mY)- ρXY (σY/σX)

который является математическим ожиданием Y при данном х

60